Image Source: http://img.thesun.co.uk
Many jobs require a good knowledge and understanding of Volume.
Medical Personnel need to administer blood and drugs in specific volumes to patients using cylindrical injection containers and intravenous drips.
Concreters need to calculate correct volumes of material required, because concrete is expensive, and it is hard to dispose of any extra left over material.
Heating and Cooling Technicians need to calculate volumes of buildings to work out what types of systems to install.
Hairdressers need to mix chemicals together in the correct volumes when making hair treatments.
Bakers and Chefs need to measure out volumes of ingredients accurately, and know how to scale these amounts up and down for making different quantities of product.
People designing and building cars need to make sure there is enough volume inside the car for occupants and their belongings to be transported comfortably and safely, as well as ensuring the volume is correct for air bags to deploy effectively during accidents.
Water authorities in cities need to make sure that there is an adequate volume of water held in dams and reservoirs.
Definition of Volume
The Volume of a 3D Shape is the number of cubes needed to fill the inside of the shape.
In mathematics we call the 3D shape a “Prism”.
A 1cm cube is about the same size as a sugar cube.
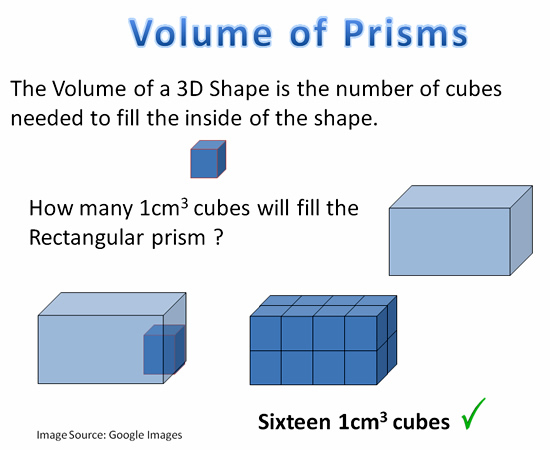
Image Copyright 2013 by Passy’s World of Mathematics
Using some simple 3D box shapes, we can investigate Volume relationships as shown in the following examples:
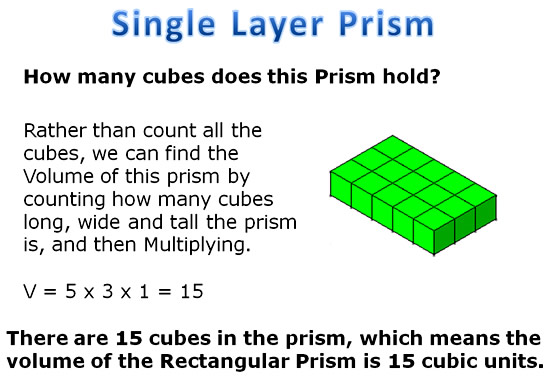
Image Copyright 2013 by Passy’s World of Mathematics

Image Copyright 2013 by Passy’s World of Mathematics
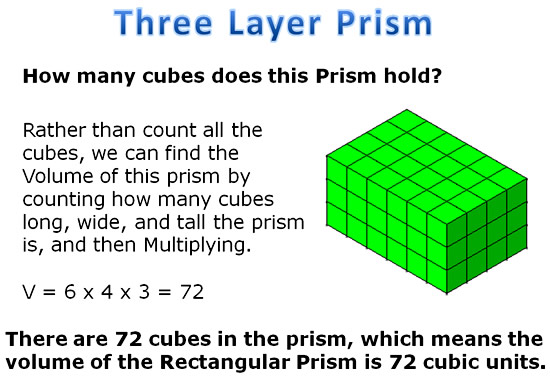
Image Copyright 2013 by Passy’s World of Mathematics
From our investigation, we can see that the volume of a 3D box shape, (called a “Rectangular Prism”), is always the LENGTH x WIDTH x HEIGHT
or the Area of the bottom layer multiplied by how many stacks high the prism is.
This means that we can use the mathematical formula of V = L x W x H, (rather than drawing and counting cubes), to work out the volume of any Rectangular Prism.
The following video shows the cubes stacking concept for working out the formula for Rectangular Prism volume
Volume of Rectangular Prisms
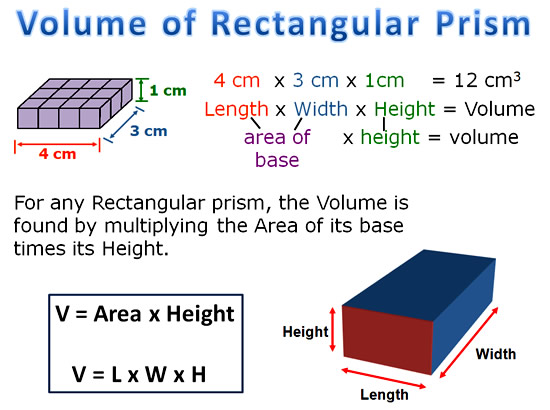
Image Copyright 2013 by Passy’s World of Mathematics
The following example shows how to calculate the volume of a box shape Rectangular Prism.
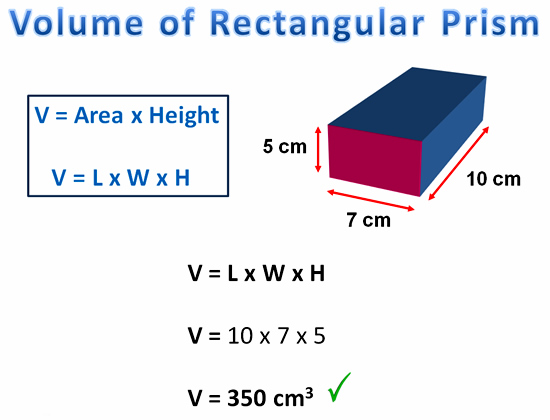
Image Copyright 2013 by Passy’s World of Mathematics
Volume of Prisms – General Formula
Mathematicians have found that for any shape Prism that has two identical ends, the Volume is always the Area of the End multiplied by how long or high the prism is.
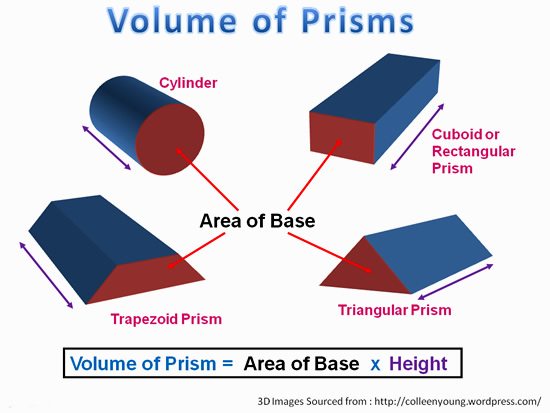
Image Copyright 2013 by Passy’s World of Mathematics
Note that when the Prism is layed on its side (like the examples above), we still call the length between the identical ends the “Height”.
This is a bit confusing. Just remember that the standard position for a cylinder (or any of these Prisms), is standing up straight like a Coca Cola can, or a tin of fruit at the supermarket, and not lying on its side.
Area Formulas that we need to use for Prism ends are the following:
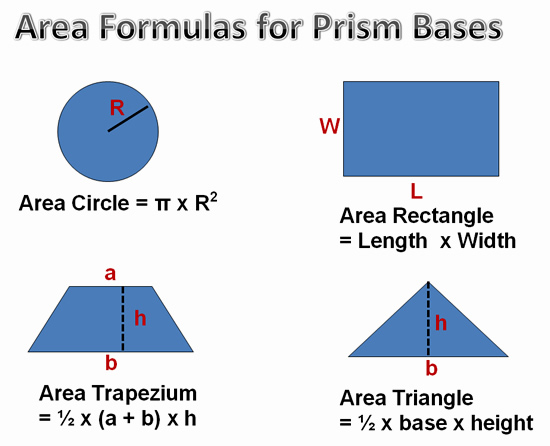
Image Copyright 2013 by Passy’s World of Mathematics
Volume of a Triangular Prism
For a prism which has triangle shaped ends, we need to first find the area of the triangle using A = 1/2 x base x height of triangle.
Once we have this area, we can then multiply it by how high (or how long for sideways prisms).
Eg. V = A x H gives us the Volume of the prism.
This is shown in the following example.
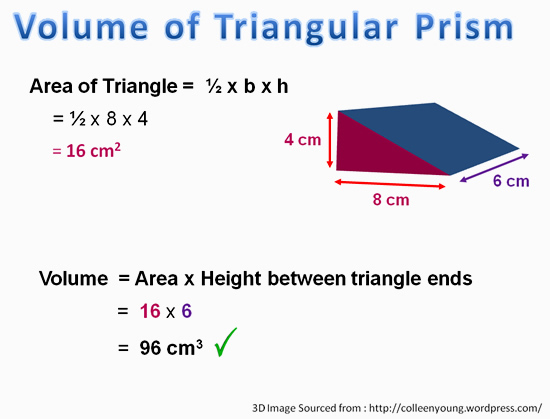
Image Copyright 2013 by Passy’s World of Mathematics
The following video shows how to calculate the Volume of Triangular Prism.
Volume of Trapezoid Prism
For a prism which has Trapezium shaped ends, we need to first find the area of the Trapezium using A = 1/2 (top + bottom) x height of trapezium.
Once we have this area, we can then multiply it by how high (or how long for sideways prisms).
Eg. V = A x H gives us the Volume of the prism.
This is shown in the following example.
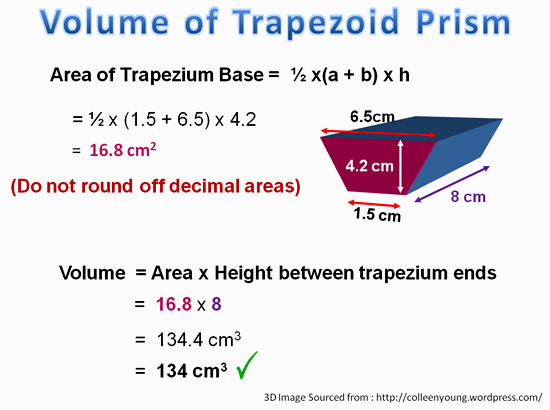
Image Copyright 2013 by Passy’s World of Mathematics
Volume of a Cylinder
For a prism which has Circle shaped ends, we need to first find the area of the Circle by Pi x Radius x Radius.
MAKE SURE THAT IF THE DIAMETER ALL THE WAY ACROSS THE CIRCLE IS GIVEN ON THE DIAGRAM, THAT YOU DIVIDE THIS DIAMETER BY 2 TO GET THE RADIUS !
Once we have this area, we can then multiply it by how high (or how long for sideways prisms).
Eg. V = A x H gives us the Volume of the cylindrical prism.
This is shown in the following example.

Image Copyright 2013 by Passy’s World of Mathematics
Volume of an Irregular Prism
Sometimes the ends of our prism are not a simple shape like a Rectangle, Square, Triangle, Trapezium, or Circle.
This means that we cannot easily calculate the area of this odd shaped end.
For these types of prisms, the area is usually given to us in the question, and we then use this area for our V = A x H calculation.
This is shown in the following example.

Image Copyright 2013 by Passy’s World of Mathematics
However, sometime we can use “Composite Areas” method to calculate the irregular area end of the Prism.
If you are not sure about what “Composite Areas” are, then take a look at our Composite Areas lesson at the link below:
http://passyworldofmathematics.com/composite-areas/
The following video shows how to do a composite areas volume calculation for an irregular “L-shaped” prism.
Volume of Prisms Formulas
For Rectangular, Triangular, and Cylindrical Prisms, we can do calculations faster by using “all in one” formulas, where the Area x Height calculation has been combined together to give a single volume formula for the 3D shape.
The following are the “all in one” formulas we can use.
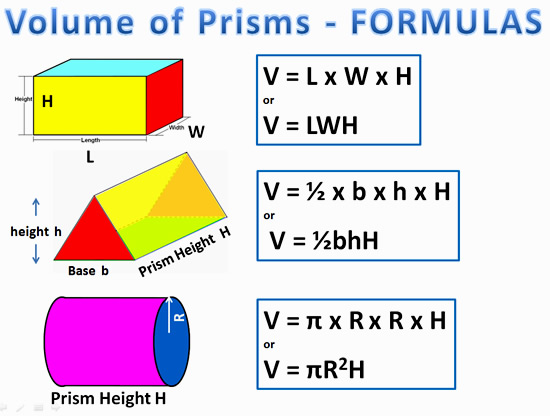
Image Copyright 2013 by Passy’s World of Mathematics
Volume of Rectangular Prism Using Formula Method
The following example shows how to use the “all in one” volume formula for a Rectangular Prism.
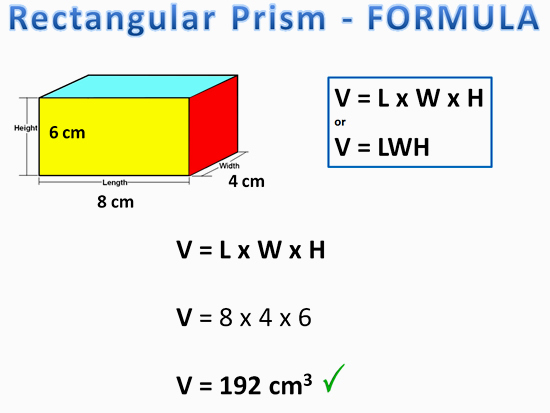
Image Copyright 2013 by Passy’s World of Mathematics
Volume of Triangular Prism Using Formula Method
The following example shows how to use the “all in one” volume formula for a Triangular Prism.
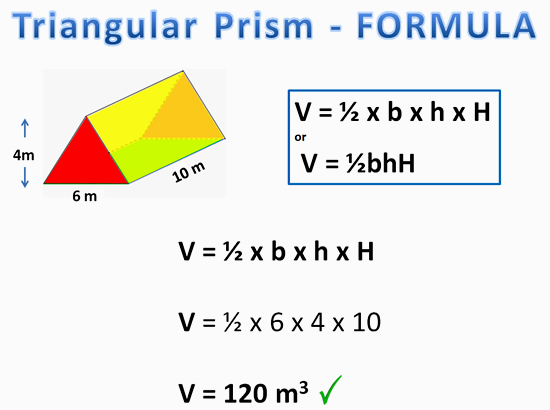
Image Copyright 2013 by Passy’s World of Mathematics
Volume of a Cylinder Using Formula Method
The following example shows how to use the “all in one” volume formula for a Cylindrical Prism.
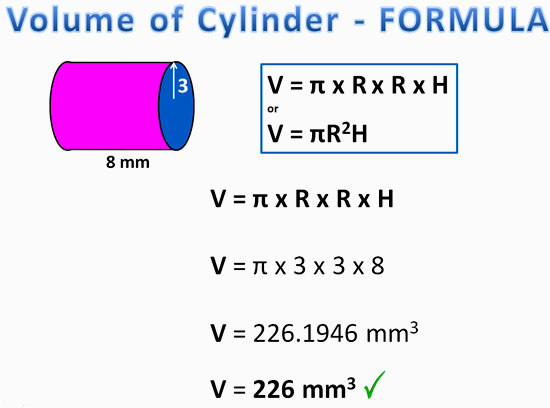
Image Copyright 2013 by Passy’s World of Mathematics
The following video shows how to calculate the Volume of a Cylinder using the Formula Method.
This next video shows how to do a practical problem about a cylindrical storage tank.
Shown in the next video is how to ESTIMATE the volume of a cylinder if you don’t have a calculator with the exact pi value on it, and you do not want to use Pi = 3.1416 and do a difficult decimal multipication by hand.
This technique is also useful for quickly checking an answer, or for eliminating unlikely letter options on a multiple choice question.
Volume and Capacity
If we have a container filled with liquid or gas,the Volume is specified in “Capacity” units.
Capacity units are Millilitres (mL), Litres (L), Kilolitres (kL) and Megalitres (ML).
This means for Liquids and Gases in containers, we do not specify their volume in cubic centimetres or cubic meters.
The container they are in is a solid structure with Volume units of cubic centimetres or cubic meters, but the liquid or gas occupying the container has a Volume that is specified in Millilitres, or Litres.
Eg. Volume is how big the container is, but Capacity is how much the container can hold.
Container size is specified in cm or m cubed, but how much liquid or gas is in the container is specified in mL or L.

Image Copyright 2013 by Passy’s World of Mathematics
As a typical example of a “Capacity” type Volume, consider a standard 375ml can of Coca Cola.

Image Copyright 2013 by Passy’s World of Mathematics
MegaLitres (ML) are a very large unit of Volume that is most commonly used to specify the Volume of Water contained in large Dams and Resevoirs.
One MegaLitre = 1 million Litres.

Image Copyright 2013 by Passy’s World of Mathematics
The following Conversion Diagram can be used for converting Capacity Units.
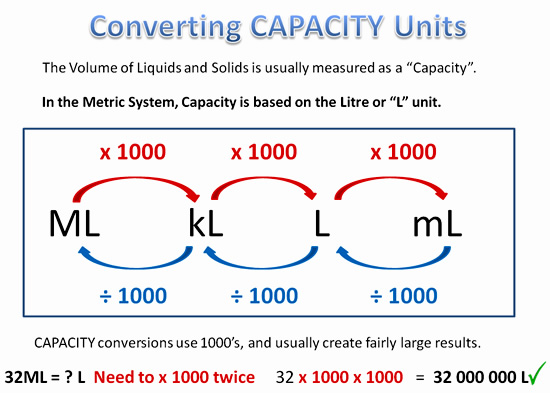
Image Copyright 2013 by Passy’s World of Mathematics
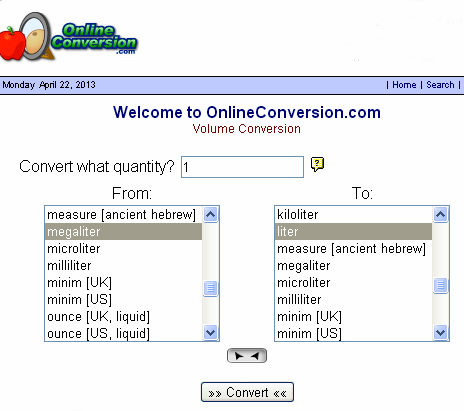
Metric VOLUME and Capacity Converter
The following web page has an easy to use online metric VOLUME and CAPACITY converter.
http://www.onlineconversion.com/volume.htm
Volume in the Real World

Image Source: http://alkispapadopoulos.com
It can be seen in the above photo that we have a rectangular prism shaped Trench, containing a cylindrical shaped Pipe.
Cement is delivered in cubic meters, and the workers would need to have calculated how much cement needed to be delivered for the job.
In this calculation they would need to have done Rectanglar Trench Volume minus the Volume of the cylinder Pipe.
If they did not do this calculation carefully and correctly, then they would either have too much cement, (which is expensive to dispose of), or not enough cement which could mean that they would not be able to complete the job on time.
Related Items
Composite Areas
Measurement Formulas
Converting Metric Measurements
Free Online Calculators and Converters
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Volume of Prisms” Powerpoint.
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy