
Image Source: http://flikie.s3.amazonaws.com
Airports can sure get busy, but not to the extent of the above photo-shopped masterpiece !
Airlines use “Hub Networks”, which are actually multiple Hub and Spoke structures that are interconnected to each other by multiple paths.

Image Source: http://www.proaerobusiness.com
In the Airline Network Routes diagram above, the large black dots represent “Hub” Airports.
Hub Airports have many connecting flights flowing through them, and so it is possible to get to any far away destination by first getting to a Hub Airport.
This means that for a person flying from one remote location to another, they can always do this in only two steps, with the middle step being a Hub Airport.
Most major airlines have multiple Hubs. Hubs allow them to offer more flights for passengers, and fill more seats on each flight, which means they are more cost efficient.
There is a good short article about Airline Networks at the following web page:
http://science.howstuffworks.com/transport/flight/modern/airline3.htm
The world’s largest Network, The Internet, is also a Network of Hubs.

Image Source: http://www.visualcomplexity.com
Efficient networks which carry a lot of traffic are always designed with plenty of hubs, as well as many connected crossing paths, so that if one path is not available between two locations, then alternative paths can be used.
The following diagram is an excellent example of a typical large scale real life network. (Click the image to go full size)
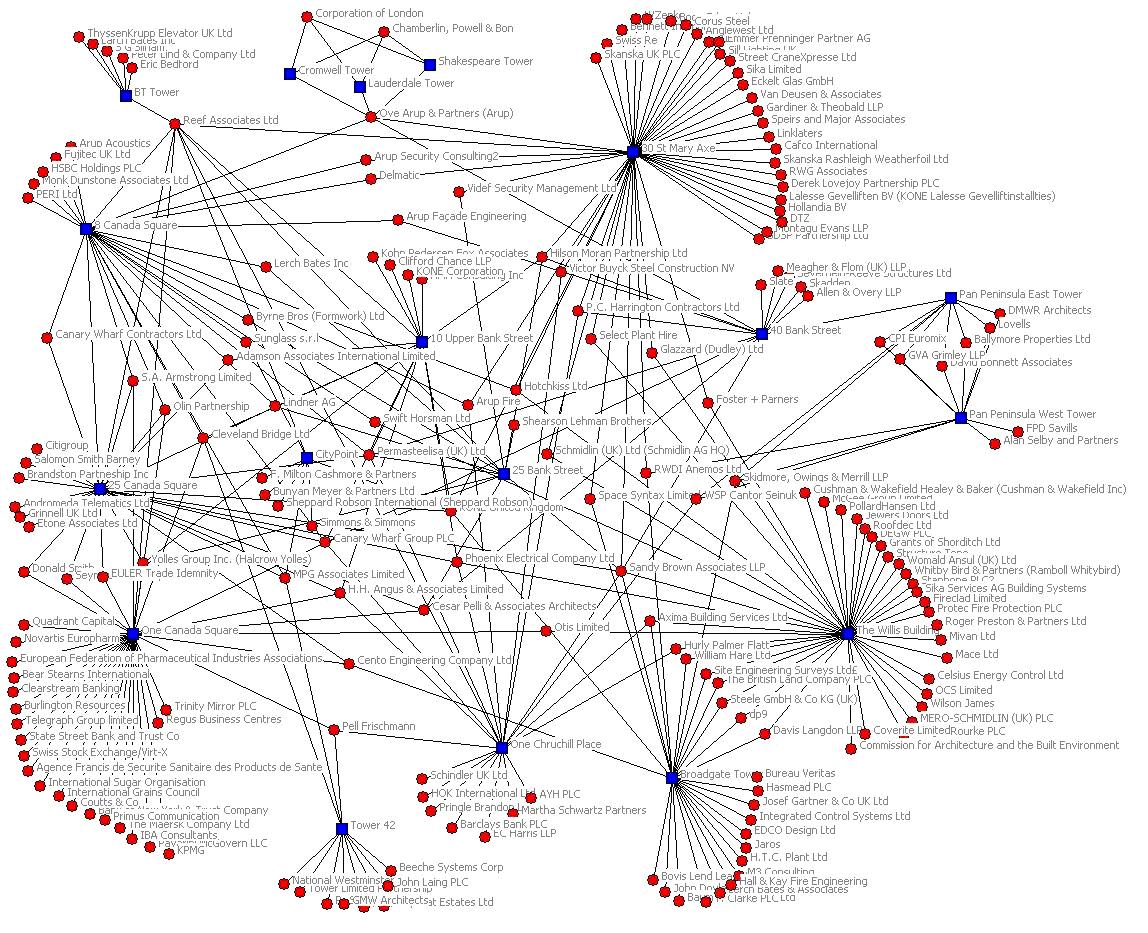
Image Source: http://4.bp.blogspot.com
Hubs and many alternative paths create a fast efficient Network for passge between any two points on the Network.
But what if we are traveling a Network and need to visit several specific points on the network one after each other?
For example, a Postman delivering items needs to visit many locations, but does not want to travel down the same street to the same location twice.
In this situation the Postman needs a different Network Structure for maximum efficiency, which is called a “Traversable” or “Transversable” Network.
In the remainder of this lesson we will be looking at the Mathematics of Traversable Networks.
Definition of a Traversable Network
A “Traversable Network” is one where we can find a route through the network, along the edges, that uses all of the edges only once.
A network is said to be traversable when it is possible to start at a “Vertex” (or “Node”), and trace out the whole network without having to retrace over any of the connector “Edges”.
The following is a Traversable Network, because we can easily get around the Network traveling along each Edge (or connector) only once.
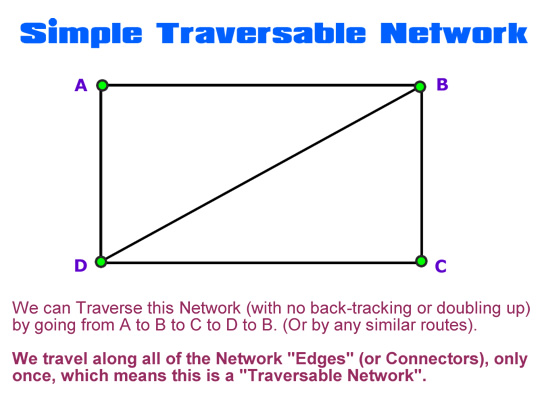
Image Copyright 2012 by Passy’s World of Mathematics
Note that when we trace fully around a Network, we do not have to get back to our starting point.
As long as we move along all connector “Edges” with no repeats, we have “Traversed” the Network. We can then say that the Network is “Traversable”.
If we manually trace around each of the following Networks, we should find that they are all Traversable.
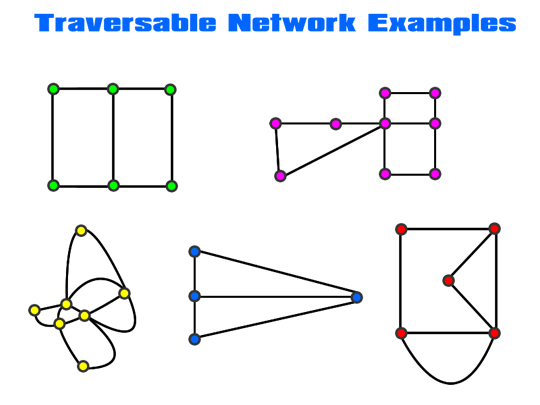
Image Copyright 2012 by Passy’s World of Mathematics
Video About Traversable Networks
The following video is a good introduction to Traversable Networks
Traversable Network Rule
The following mathematical rule overcomes the difficulties of trying to manually trace a unique traversable path through any Network.
It is far easier to do some calculations and apply this rule, than to do complicated manual tracing.
For a network to be traversable, it must be fully connected.
A connected network is traversable if:
all vertices are of even degree; or
exactly two vertices are of odd degree and the rest are of even degree.
If a network has more than two vertices of odd degree, it is not traversable.
(Information Source: http://coburgmaths09.global2.vic.edu.au/ )
The “Degree” (or “Level”) of a vertex is how many Edges are connected into it.
If we go back to our previous Traversable Network examples, we can see that they are all Connected Networks.
We can then label the “Degrees” for each Vertex, and see that they all follow the above Traversable Rule.
This is shown in the following diagram.
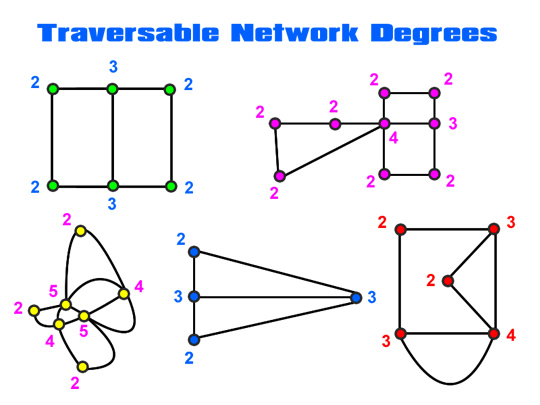
Image Copyright 2012 by Passy’s World of Mathematics
All of the Networks in this diagram are connected Networks.
All of the Networks have no more than two Odd numbered Degrees (or Levels) values on their Vertices.
We can also manually trace over these Networks by hand, and see that they are indeed Traversable. Eg. For each Network we can find a route which passes along all of the Edge paths, without repeating any of the paths.
Hint: When manually tracing over a traversable network by hand, which has odd degree vertices, always start at one of the odd vertices.
Traversable Network Questions
Using the Connected Degrees Rule, find out which of the following Networks are Traversable.
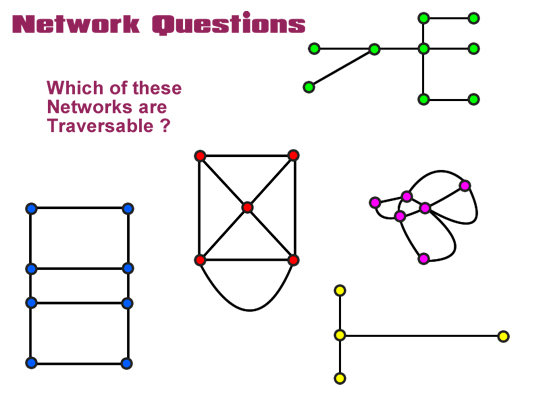
Image Copyright 2012 by Passy’s World of Mathematics
Answers to Traversable Network Questions
The Green and Yellow Networks cannot be Traversable, because they are not fully connected Networks. They each have several end point Vertices of Degree 1, which also breaks the “not more than two odd numbers” rule. Finally we cannot manually trace along all the “Edge” connectors of these Networks without doing repeats. They are both definitely not Traversable.
The Blue, Red, and Pink Networks are shown below with their Vertex Degrees labelled.
(Remember the “Degree” or “Level” of each Vertex dot, is the number of connector Edges attached to that Vertex dot.)
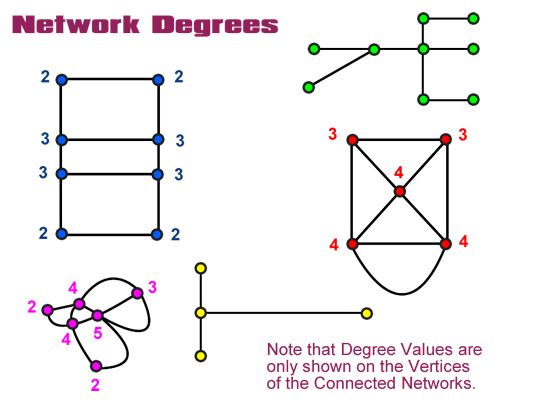
Image Copyright 2012 by Passy’s World of Mathematics
The Blue Network is not Traversable because it has more than two vertices of odd degree. Eg. There are four vertices with Degree equal to the odd number 3, and we are only allowed to have a mximum of two odd numbered Vertices.
The Red Network is Traversable, as it only has two Vertices of odd Degree “3”, and the rest of its vertices are even numbered values.
We can fully Traverse the Red Network with no repeats if we start at the end of the loop, go around the loop, and then up and around the square following its trianges.
The Pink Network is Traversable because it has only two Vertices of odd Degree (“5” and “3”), and the rest of the vertices are even number values.
We can manually traverse the Pink Network, but finding the exact route which is Traversable is fairly challenging.
Networks and Six Degrees of Separation
The Mathematics of Networks involves a wide variety of everyday situations from social interactions to biochemistry.
The following video covers the idea of hubs in Networks making any member of the network separated from another member by a maximum of six connections.
Additional Information
The “Coburg General Maths” site on Edublogs has some great notes on Networks for Senior High School Students:
http://coburgmaths09.global2.vic.edu.au/networks-content-page/
The following web page by Sonja Stankovic has an excellent solution to the classic “Konisberg Bridges Question”, as well an interesting Network Question on Airline Flight Routes.
http://sonjastankovic.wordpress.com/2008/08/10/graphs-part-1-introduction/
Related Items
Introduction to Network Mathematics
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Enjoy,
Passy


