Could this be Melbourne’s worst million dollar mathematics mistake?
A huge Gabion retaining wall that was being built near where Passy lives crashed down in spectacular fashion a couple of days ago.
Here is a YouTube video of the aftermath.
The Olivers Hill Gabion Wall
We have been watching this wall being built over the last two months, and it looked to us like it was being built far too high without enough base thickness to support the weight of the rocks on top.
The angles, thickness, staggering, and terracing did not look to be correct. The fact that there was no stepping or terracing on such a high wall is very puzzling indeed.
Initially the wall was tilted back into the hillside at an angle, but we had noticed in the last week that the wall seemed to be getting more and more vertical as it got higher.
The wall was built several metres out from the cliff face, and the gap between the two was recently filled with soil that was brought in from elsewhere.
It appears that the weight of this filling soil may have caused a failure along the bottom of the wall, and the whole middle section then collapsed. Local residents said they saw the bottom sections of the wall beginning to buldge outwards several hours before the disaster. Miraculously nobody was killed or injured.
Here at Passy World, we suspect that “Internal Bearing Failure” in the wall itself is probably the root cause of the disaster.

Image Source: http://www.limitstate.com
The bearing capacity of the bottom rows of baskets was possibly not strong enough to hold the baskets stacked above them, along with the weight of the soil behind them.
If they do find out the exact cause the failure and the information is made public, we will supply an update.
Another serious issue we have with the Gabion Wall involves it being built about 500 meters away from the sea shore of Port Phillip Bay. What is the life expectancy of its basket wire openly exposed to such salty corrosive conditions ? If the wire rusts away, won’t the whole wall come tumbling down onto the adjacent seaside highway, in just a few short years time ?
The wall was being built by the State Government roads authority here in Melbourne, and so far has cost local taxpayers over one million dollars. A recent article on the Internet put the exact cost at 1.4 million dollars.
In this lesson we look at how Gabion Walls are supposed to be constructed, and the Mathematics of Gabion Wall Design.
About Gabion Walls
“Gabions” are rectangular stone filled baskets used to stabilize soil and prevent erosion. The baskets are stacked on top of each other to form retaining walls.
They have been used since Egyptian times and were first made of woven reeds and rock and used to stabilise the banks of the river Nile.
Here is what a typical empty Gabion basket looks like.

Image Source: http://www.biztrademarket.com
The Olivers Hill wall which collapsed was being built with the wire being meshed onsite, like in this picture of a wall being built elsewhere in the world.

Image Source: http://images.tradekool.com
Another method of building such walls is to use solid welded stainless steel baskets like in this example.

Image Source: http://www.greenfab-media.com
Here is a Gabion Wall in New York State USA.

Image Source: http://www.raconsultantsnj.com
Notice that this wall is angled back into the hill and stepped with terraces.
The Olivers Hill wall which collapsed was not built like this.
Here at Passy World we are very surprised that the bottom of the Olivers Hill wall was not thicker, and that the Olivers Hill wall was not stepped with terraces.
More information about Gabion Walls can be found at the following links:
http://en.wikipedia.org/wiki/Gabion
http://www.gabions.net/index.html
http://www.limitstate.com/geo/gabion-walls
Mathematics of Gabion Walls
There is a great design article about Gabion walls at the following link:
http://www.hy-tengabions.co.uk/technical_publications/design_guide.pdf
The mathematics and design is quite complicated because of the following factors:
The underlying ground and soil has to support the weight of the wall
The weight of the baskets needs to be able to hold back any unstable soil and rock geology that is behind the wall
The wall needs to be a stable self supporting monolith
Complex Geometry, Algebra, and Physics are involved with the successful construction of a Gabion Wall.
Here are some screen shots of some of the mathematics involved, taken from the “Hy-Ten Gabions” design document, and modified slightly by Passy’s World.
First of all we need to know the total weight of the wall.
( The funny “E” looking symbol is “Sigma” which means to add up all the courses or rows of the wall to a grand total.)

Image Source: http://www.hy-tengabions.co.uk
The Centre of Gravity of the Wall is also important. Here is part of the calculation:
Image Source: http://www.hy-tengabions.co.uk
The thrust pushing force of the soil behind the wall needs to be known.

Image Source: http://www.hy-tengabions.co.uk
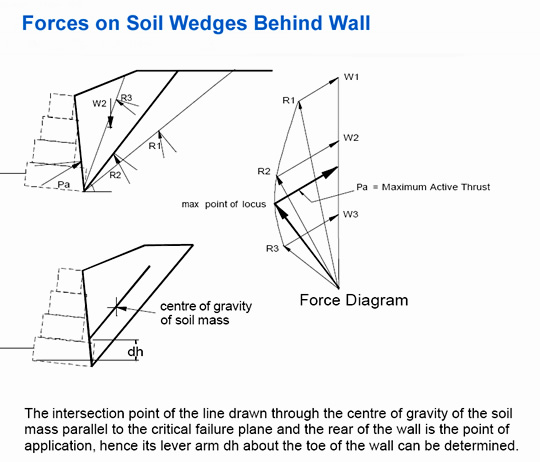
The thrust of the soil is examined using wedge models of the soil that is behind the wall.
Image Source: http://www.hy-tengabions.co.uk
The stability of the wall involves a number of calculations that determine if the weight and angle of the wall is going to counter-balance the weight of soil behind it.
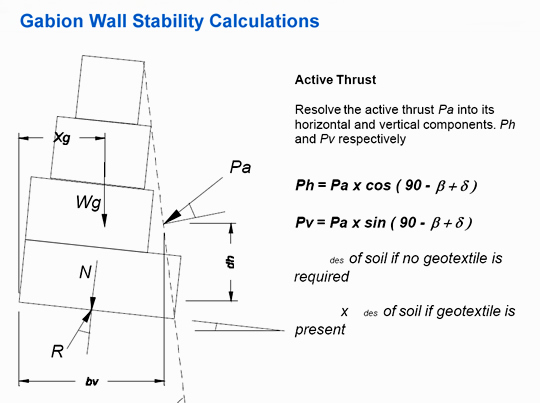
Image Source: http://www.hy-tengabions.co.uk
One of the stability calculations that is done is to see if the wall baskets will slide apart from each other when pushed from behind.

Image Source: http://www.hy-tengabions.co.uk
There are many other calculations used to determine if a Gabion wall will work or not.
The “Hy-Ten” design document at the following link contains all of the information.
http://www.hy-tengabions.co.uk/technical_publications/design_guide.pdf
Gabion Wall Design Using Computers

Image Source: http://www.limitstate.com
When the mathematics is quite complicated, like it is for Gabion Walls, it is programmed into computers to work out whether a man made structure will be effective.
One of the leaders in this area appears to be a company called “Limit State”:
“LimitState develops software products and supplies training courses, seminars and related consultancy services for structural and geotechnical engineers. Innovative software products use novel computational limit analysis techniques to rapidly and robustly analyse the ultimate (collapse) limit state.”
For more information, and to see some great animations about ways that Gabion Walls can fail, visit their site at:
http://www.limitstate.com/geo/gabion-walls
Epic Mathematics Fail

Image Source: http://www.frankstonweekly.com.au
It would appear that somewhere in the design of the Olivers Hill Gabion Wall a critical mathematical mistake was made.
As we have seen the mathematics involved is very complicated.
The Engineers designing the walls would need to be good mathematicians, and their design values would need to be double checked by computer programs and other Engineers.
If we were building a Gabion Wall, we would look at getting some engineering experts in to help – people who are very familiar with these calculations, and have built these types of walls before.
It certainly makes Australia look very third world when Engineering Projects like this fail in such spectacular fashion.
The even bigger fail is that one million dollars of taxpayers money has fallen down in a heap, and it is probably going to cost more than another million dollars of public money to clean up the mess and redo the project.
Related Items
Mathematics of Aircraft and Train Disasters
If you enjoyed this post, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our blog, then please email us at the hotmail address shown in the right hand side bar of this page.
Enjoy,
Passy





Pingback: Coffee Spill Mathematics | Passy's World of Mathematics
Pingback: Mathematics of the Melbourne Cup | Passy's World of Mathematics