
Graphics Sourced from Google Images
This fun game teaches students to get very good at plotting (x,y) points, as well as reading points on the Cartesian Plane, and it is lots of fun.
The game was developed here at Passy’s World by Passy and Jack, and has been trialed in classrooms with great results. (Thanks to Jack for coming up with most of the ideas on this one!).
There is a PPT Presentation for this Game which will be very useful for instructing the students on how to play the game.
Overview of Game
Students plot 20 points of their choice on a Cartesian X-Y Grid, which ranges from -6 to 6.
A special Positive / Negative Virtual Dice is rolled, to generate a “Bingo Coordinate”.
If a student finds they have that coordinate marked down, they circle it in red pen on their grid.
(Repeat drawing Bingo Coordinates by rolling the special dice)
Once a student has FIVE Coordinates circled anywhere on their Grid, they call out BINGO, and get their grid checked and win a prize.
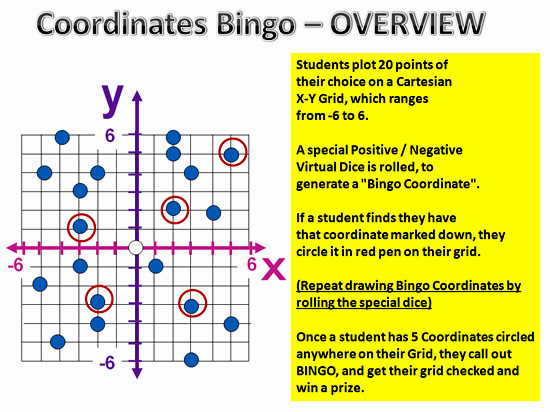
Image Copyright 2013 by Passy’s World of Mathematics
Equipment Required for Bingo Coordinates
Grid Paper / Graph Paper (one per student)
PPT Presentation (See end of this lesson for Details)
Laptop PC and Data Projector (for Virtual Dice and PPT)
Lollipops or individually wrapped candy / lollies for Prizes.
Instructional PowerPoint
This is available for free to any Subscriber to Passy’s World of Mathematics.
Becoming a Subscriber is Free.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
You will be able to project the PowerPoint Instructional Slides in your classroom to show the students how the game works.
Once you are a Subscriber, Simply email us at the address shown below, and ask for a copy of the “Coordinates Bingo” PowerPoint.
Becoming a subscriber to Passy’s World is free, and to find out what happens when you subscribe, click the link below:
Setting Up the Grid Paper
Students Rule up an X-Y Axis on their Grid Paper that forms a 6×6 Grid like the one shown below.
We need a 6×6 Grid because we will be rolling Dice to generate the Bingo Coordinates.

Image Copyright 2013 by Passy’s World of Mathematics
If you need some printable Grid Paper, then try the following links:
Four to a Page Cartesian Grids
Picking Points – Pre-Game Discussion
Students will need to plot 20 different random points of their choice onto their Grid.
We will be rolling dice to generate the Bingo Game Coordinates, and they will have to hope they get lucky, and some of the Dice Coordinates match their coordinates.
(We have found that 20 points makes for a game that goes for about 20 minutes and shopuld have at least 6 winners).
(You can also award some tasty treats for good answers during this pre-game discussion).
BEFORE THEY PICK THEIR POINTS – GO THROUGH THE FOLLOWING:
See if the students can figure out how many different points there are on the Grid.
ANSWER: The Grid is 12 x 12 = 144 possible points.
But what if we allowed Fraction and Decimal Coordinates ?
ANSWER: Infinite
For our game we are only using whole number integer coordinates – you can plot fractions or decimals if you like, but they will never come up on the dice!
There are certain whole number points on the Grid which should not be used – What are they ?
ANSWER: X-Axis points like (1,0) (-3,0) etc and Y-Axis Points like (0,2) (0,-5) etc as well as the Origin – because these coordinates have a zero in them, and zero can never come up on a Dice!
So how many usable points are there on our Grid for the Game ?
ANSWER: 144 – 6 – 6 -6 – 6 -1 (for the origin) = 144 – 25 = 119
So what are the chances of one of your coordinates being called as a Bingo Coordinate ?
ANSWER: 20 / 119 which is roughly 1/6 .
Note that the Game was not deliberately designed to make the chances 1/6 on the Grid, be the same as the Dice Chance; and if we played with only 10 coordinates, the chance for each one coming up would be 1/12.
What are the chances of a Bingo Coordinate coming up; AND then on the very next dice roll, the exact same coordinate coming up again ?
ANSWER: 1/6 x 1/6 = 1/36
Note from classroom trials, the game usually ends with no repeat Bingo coordinates happening during the whole 20 minute game.
Now get the students to mark on their grid their 20 chosen coordinates.
Their finished competition entry should look something like this:
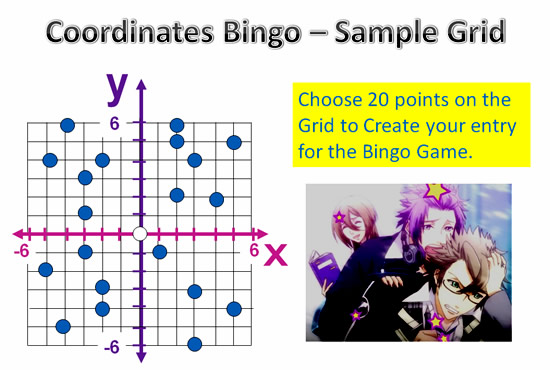
Image Copyright 2013 by Passy’s World of Mathematics
Note the anime girl in the above image is upset because she just noticed that her friend plotted lots of her entry’s points on the X and Y Axis!
Positive and Negative Virtual Dice
The virtual dice which are needed to play the game can be found at the link shown below.
Two rolls need to be done for each coordinate, the first roll is the X-coordinate, and the second roll is the Y-coordinate.
The teacher, or a reliable student, needs to note down each coordinate which is rolled during the game, and also plot the Dice Rolled Coordinates on a Grid, for later answer checking.
Click the following link to access the virtual dice
Positive and Negative Virtual Dice App
Note that an alternative would be to use a Coin with a real Dice (Head = Positive, Tails = Negative)
Playing The Game
Project the Virtual Dice App onto a Screen at the front of class.
Roll the Virtual Dice once for the X-Coordinate, and one again for the Y-Coordinate,
Call out the resulting (x,y) Coordinate
(Teacher or an appointed student needs to note down the coordinate, and also plot it on the answer grid)
If a student has that coordinate they circle it in red pen
Keep rolling the dice until a student has 5 coordinates and calls out Bingo
Check the Student’s entry and award a prize
Keep playing for about 20 minutes until about 10 prizes have been awarded.
Positive Coordinates Game
Our Bingo Game can easily be adapted for beginners doing only Positive Coordinates.
Make a 12 x 12 Y-X Grid, which has (0,0) in the bottom left hand corner, and (12,12) in the top right hand corner.
Then use Two Dice to generate the coordinates.
There is a virtual Dice for this at the following link:
Click here for Virtual Double Dice App
Note that the game will be a little biased towards Coordinates containing 7’s, because 7 is the highest probability result for rolling two dice.
(Eg. 2 and 5, 6 and 1, 3 and 4, 4 and 3, 5 and 2, 6 and 1 = 6/36 = 1/6; whereas 12 is only from 6 and 6 which is a 1/36 chance).
See if this becomes apparent at all, as the game progresses.
Play the rest of the game as normal – Roll the two dice and add the result to get the X Coordinate, then roll them again to get the Y-Coordinate.
Note that Coordinates containing Zero or One will never come up in the Bingo Coordinates, because the lowest possible result from two dice is 1+1 = 2
Related Items
Gradient and Slope Formula
Gradient and Slope
Gradient and Slope in the Mountains
The Cartesian Plane
Plotting Graphs from Horizontal Values Tables
Plotting a Linear Graph using a Rule Equation
Plotting Graphs from T-Tables of Values
Finding Linear Rules
Distance Between Two Points
Mountain Gradients
Real World Straight Line Graphs I
Real World Straight Line Graphs II
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Coordinates Bingo Game PowerPoint”
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Like Us on Facebook
Our Facebook page has many additional items which are not posted to this website.
These include items of mathematical interest, funny math pictures and cartoons, as well as occassional glimpses into the personal life of “Passy”.
Check it out at the following link:
https://www.facebook.com/PassysWorldOfMathematics
While you are there, LIKE the page so you can receive our FB updates to your Facebook News Feed.
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy





