
Image Modified from www.chiropractic.com
Linear Rules or Functions are mathematical algebra equations which tell us how to get the output Y-values for a given set of input X-values.
The Rule tells us the “Relationship” between all of the x and y values.
If we graph any of these input and output (x,y) values, a straight line will be created.
We need to be able to find the Rule for Sets of (x,y) pairs, and for any straight line graphs we have drawn, so that:
1) We can find the “Y” values for very large x-values, without having to draw a giant graph and manually read them off
2) We can find the “Y” values for very small x-values, like x = 0.001, which would be way too small to try and read off a normal sized graph
3) We can type the rule into a Computer Graphing Application, and have the computer draw the graph for us
In relation to point 3) above, nobody draws graphs in the real world any more, they are all drawn by computer apps.
If you would like to try out an Online Graph Maker, then try the ones out at these two links:
http://webgraphing.com/plotting_basic.jsp#
http://rechneronline.de/function-graphs/
Real World Straight Line Graphs
If you would like to see where straight lines are used in the real World, then have a look at our lessons about this at the links below:
http://passyworldofmathematics.com/real-world-line-graphs/
and
http://passyworldofmathematics.com/straight-line-graphs/
Types of Linear Relationship Rules
There are basically 3 types of Linear Rules:
1) Simple Addition or Subtraction
Eg. y = x +2, y = x -5, y = x + 7, y = x -3 etc
2) Simple Multiplication or Division
Eg. y = 2x, y = -5x, y = x/2, y = -x/5 etc
3) Combination Rule using y = mx + c
Eg. y = 2x + 3, y = -3x + 1, y = 4x -2, y = -x + 7 etc
When we are given a Table of Input and Output x and y values, we check for:
1) Simple Addition or Subtraction
and if this does not work out then check for
2) Simple Multiplication or Division
and if this does not work out then check for
3) Combination Rule using y = mx + c

Image Source: http://media2.newsobserver.com
Think of this as being like a Doctor in a Hospital Emergency Ward checking an incoming patient’s injuries.
They might check for :
1) Do they just have some cuts and bleeding
2) Do they just have broken bones
3) Do they have a combination of injuries
Just like the Doctor case, if we have situation 3), involving a combination of issues, then this situation will require the most work.
Simple Addition Rule
In this situation the difference between the y and x values will be the same number every time as we work down our set of (x,y) values.
If we cannot identify this relationship by simply looking at the numbers, then we can mathematically check for it.
We check by adding an extra “y-x” column to our given table of input “x” and output “y” values, and then doing the math.

Image Copyright 2013 by Passy’s World of Mathematics
In every case the y-x difference is always the same number value
of positive “1”.
The Linear Rule is y = x + 1
Check:
y = x + 1 (sub in our x,y is 0,1 value)
1 = 0 + 1
1 = 1
Our y = x + 1 rule works, and so our y = x + 1 answer is correct!
Zero Addition Rule
If the X-Y difference check produces zeroes, then we have the y=x rule.

Image Copyright 2013 by Passy’s World of Mathematics
This relationship should be obvious by just looking at the x and y values and seeing that they are the same.
We do not really need to do the Y-X column maths.
Simple Subtraction Rule
This is the exact same approach as the Simple Addition Rule, but our y-x values all come out the same NEGATIVE NUMBER each time.

Image Copyright 2013 by Passy’s World of Mathematics
In every case the y-x difference is always the same number value of NEGATIVE 2 OR “-2”.
The Linear Rule is y = x + -2
which we write as y = x – 2
Check:
y = x – 2 (sub in our x,y is 0,-2 value)
-2 = 0 – 2
-2 = -2
Our y = x – 2 rule works, and so our y = x – 2 answer is correct!
If we do not find a simple Addition or Subtraction Rule that works for our (x,y) points, then we need to move on to checking for a Simple Multiplication Relationship.

Image Copyright 2013 by Passy’s World of Mathematics
Simple Multiplication Rule
If there is a specific number that we can multiply each x value by, and this produces the y-value, then we have a Multiplication Relationship.
In this situation y divided by x for all values will be the same number every time, EXCEPT FOR X = 0
(It is impossible to divide any number by zero, and so we have written “–” in our table).
If we cannot identify this relationship by simply looking at the numbers, then we can mathematically check for it.
We can check for a “Multiplication Relationship” by adding an extra “y/x” column to our given table of input “x” and output “y” values, and then doing the math.

Image Copyright 2013 by Passy’s World of Mathematics
In every case y/x is always the same number value of positive “3”.
The Linear Rule is y = 3x
Check:
y = 3x (sub in our x,y is 1,3 value)
3 = (3)(1)
3 = 3
Our y = 3x rule works, and so our y = 3x answer is correct!
Simple Multiplication – Negative Values
Note that y/x can come out a negative number, such as -2.
If this happens the Linear Rule is y = -2x

Image Copyright 2013 by Passy’s World of Mathematics
Simple Multiplication – y/x value is 1
The y/x value can sometimes turn out as “1”.

Image Copyright 2013 by Passy’s World of Mathematics
If this happens the Linear Rule is y = 1x
which we write as:
y = x
Simple Division Rule
If our y/x values from a Simple Multiplication checking table turn out to be all the same fraction value, then we have a Simple Division Linear Rule.

Image Copyright 2013 by Passy’s World of Mathematics
The same y/x value we get each time is 1/4 .
Our Linear Rule is: y = 1/4 x
We can write this as: y = x/4
Combination Rule: y = mx + c
If we cannot identify a simple Addition, Subtraction, Multiplication, or Division relationship, then there is probably a “Combination Rule” involved.
Eg. If our y-x values, and our y / x values, do NOT give us a common number answer pattern, then we probably have a more complicated “Combination Rule” involved.

Image Copyright 2013 by Passy’s World of Mathematics
Combination Rules are more complicated, and involve both Multiplying and Adding to make a rule in the form:
y = mx + c or y = mx – c
where m = gradient, and c = y-intercept
Note that Americans, and some other countries, call the combination rule
y = mx + b and y = mx – b,

Image Copyright 2013 by Passy’s World of Mathematics
Combination Rule – Working Out Steps
There are four steps, as follows:

Image Copyright 2013 by Passy’s World of Mathematics
Step 1 involves working out the Change in x and y values.

Image Copyright 2013 by Passy’s World of Mathematics
Step 2 involves Calculating the Gradient or Slope as:
m = Change in Y / Change in X

Image Copyright 2013 by Passy’s World of Mathematics
If we have a Graph given to us, instead of an x,y Values Table, then we need to find the gradient “m” directly from the graph.
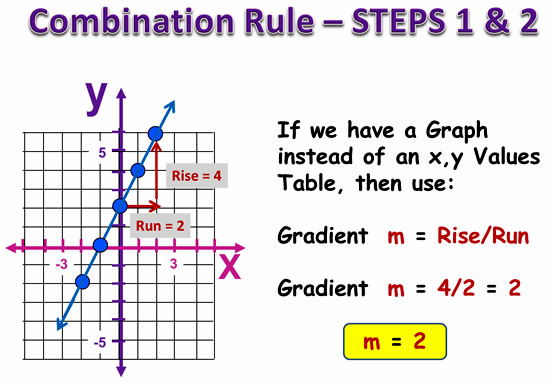
Image Copyright 2013 by Passy’s World of Mathematics
Now let’s look at Steps 3 and 4, where we find the “C” value for y = mx + c

Image Copyright 2013 by Passy’s World of Mathematics
People have a lot of trouble with this step, because it looks like there is too much working out to do.
Another way to approach Step 3 is to realize that we have half the rule already, because we know m = 2.
This means the Y values are all 2x + ?
If we now go back and visually inspect the X and Y-values Table, knowing that we need to double each “x” value and then also do something else,
we might be able to figure out what that something else is.
Once we figure out this something else is “adding 1” then we know that C = + 1, and the full rule is y = 2x + 1.
Once we have completed Steps 1 to 3, we know the number values for “m” and “c”, so all we need to do is put these values into y = mx + c

Image Copyright 2013 by Passy’s World of Mathematics
As we discussed above, once we know the gradient “m” we can look at the table values and should be able to figure out “c”.
We combine Steps 3 and 4 together into a single step:
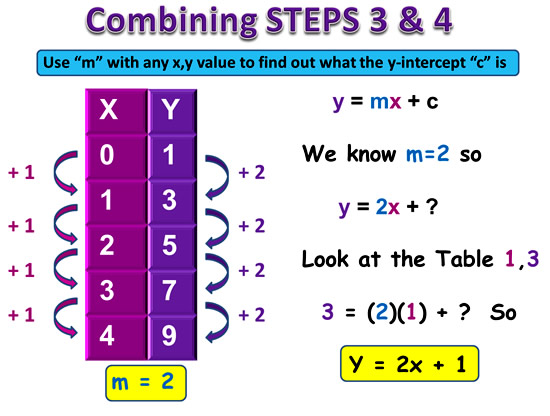
Image Copyright 2013 by Passy’s World of Mathematics
Video About Finding y = mx + c Rules
Finding y = mx + c rules is not easy for beginners, and it might take a while until you fully figure out what is going on.
Watching the following video will help you better undertand what needs to be done for these types of questions.
Finding Rules for Line Graphs
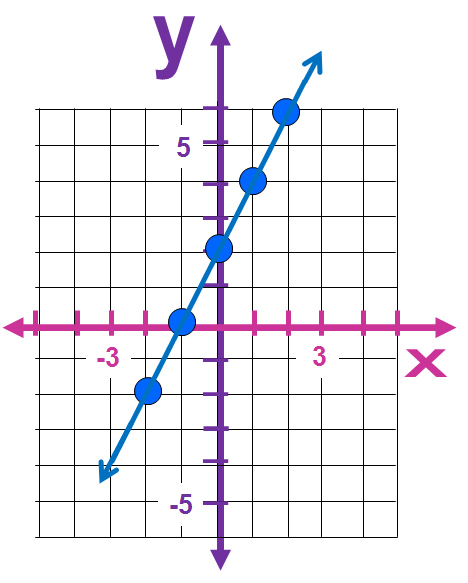
Image Copyright 2013 by Passy’s World of Mathematics
When we have a Line Graph, the procedure is the same, except that our (x,y) points are on the line, rather than being in a values table.
The Procedure is:
Find the Gradient “m” between any two points on the line using Rise / Run
(The points are best located where the line crosses the corners of a set of four grid squares, so that we have whole number values for Rise and Run).
We then put our number value for “m” into y = mx + c, and use a set of x,y point values from the line to work out the value of “c”.
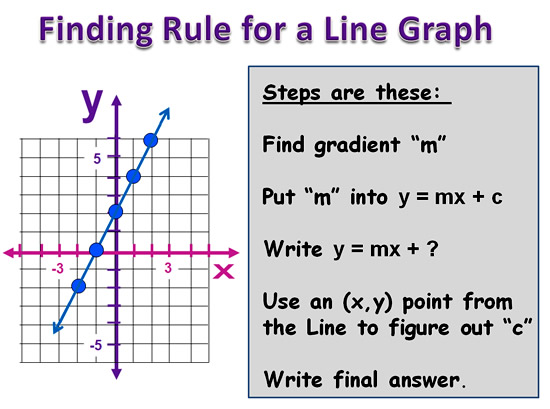
Image Copyright 2013 by Passy’s World of Mathematics
Finding Rule for Graphs – Example One
In the example below, we find the Gradient slope, and then from there on we have half the rule done.
All we need to do is work out what else is done to “x” to get the “Y” value, and this will tell us what “c” is.
Gradient “m” is always the multiply part of the rule, and “c” is always the add on or subtract part of the rule.
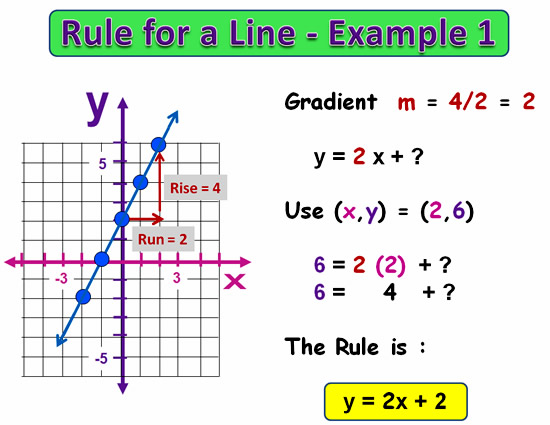
Image Copyright 2013 by Passy’s World of Mathematics
Finding Rule for Graphs – Example Two
In this next example, we do the same procedure:
First use “m” = Rise / Run to get the first part of the rule.
Then pick any point from the line, multiply the “x” coordinate by the “m” value, and then figure out what we need to add on, (or subtract away), to get the Y-Value.
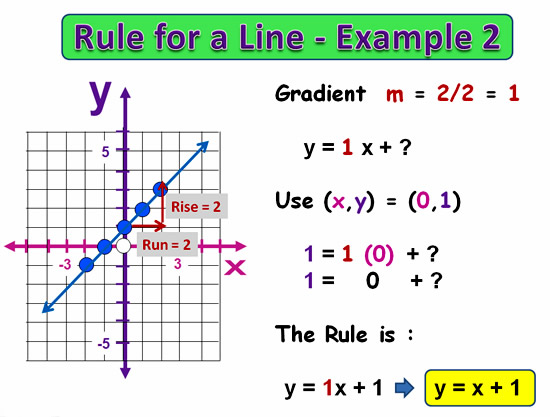
Image Copyright 2013 by Passy’s World of Mathematics
The above example shows that we can use the Combination Rule y = mx + c for any type of straight line.
The Example 2 line was actually a simple “Addition Rule” relationship.
Even though we went through the more complicated “Combination Rule” steps, we still got to the correct answer.
Blank X-Y Grid
Here is a blank X-Y Grid you can print out and use for drawing question lines onto and working out rules.
Image Copyright 2013 by Passy’s World of Mathematics
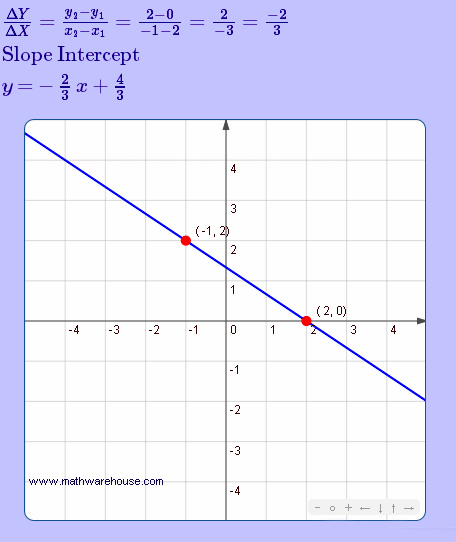
Linear Rule Generator
The Maths Warehouse website has a great free java app on their page where we can move around the given straight line, and the appp works out the y = mx + c (as y = mx + b) rule for us.
It can be found on the following web page:
http://www.mathwarehouse.com/algebra/linear_equation/slope-intercept-form.php
Related Items
The Cartesian Plane
Plotting Graphs from Horizontal Values Tables
Plotting a Linear Graph using a Rule Equation
Plotting Graphs from T-Tables of Values
Real World Straight Line Graphs I
Real World Straight Line Graphs II
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Linear Relationships Rules” Powerpoint.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Like Us on Facebook
Our Facebook page has many additional items which are not posted to this website.
These include items of mathematical interest, funny math pictures and cartoons, as well as occassional glimpses into the personal life of “Passy”.
Check it out at the following link:
https://www.facebook.com/PassysWorldOfMathematics
While you are there, LIKE the page so you can receive our FB updates to your Facebook News Feed.
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy





Pingback: Distance Between Two Points | Passy's World of Mathematics
Pingback: Gradient and Slope | Passy's World of Mathematics
Pingback: Midpoint Between Two Points | Passy's World of Mathematics
Pingback: Rocket Science and Cars | Passy's World of Mathematics
Pingback: X and Y Intercepts | Passy's World of Mathematics
Pingback: Coordinates Bingo Game | Passy's World of Mathematics
Pingback: Gradient Slope Intercept Form | Passy's World of Mathematics