Zero and Negative Exponents

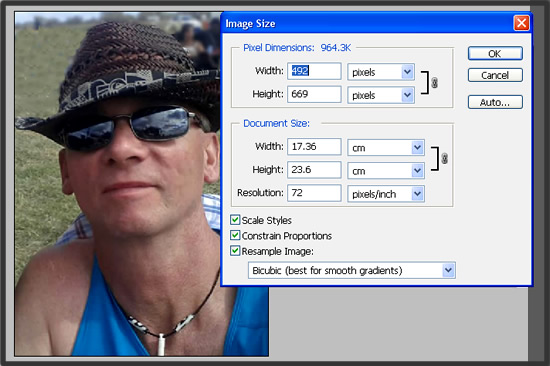
Image Copyright 2013 by Passy’s World of Mathematics

In the above screenshot, we are using Adobe Photoshop to shrink down a large digital camera photo to one quarter of its original size.

We need to do this so that the photo can fit and load faster onto Facebook, or any other website we put it on.

Note that we can put full size digital camera photos onto the Web, but one of two things usually happens:

The App we upload the program with does the shrinking for us, but a lot of times not as well as we could do it ourselves in Photoshop

or

The App does not shrink the photo and the very large photo takes a long time to download and be resized by our web browser, and thereby makes the web page it is on load a lot slower.

So “Do the Math”, and always try to “optimise” the size and quality of any images, before you put them up onto the web.

Did you know that a computer cannot actually do Fractions or Percents during its processing?

To figure out what one quarter equals, at a low level the computer actually uses negative powers of 2, (associated with the “Binary” processing that all computerised devices use).

If it wasn’t for Negative Exponents, we would not have much of the wonderful photo processing that is currently available.

Negative Exponents which result in Power Fractions are also associated with “Exponential Decay”.

If you would like to find out more about Exponential Decay, then check out our previous lesson about “Exponents in the Real World” at the link below:

Click Here to Learn About Exponential Decay

Today’s Exponents lesson is all about “Negative Exponents”, ( which are basically Fraction Powers), as well as the special “Power of Zero” Exponent.

Power of Zero Exponent

We can work out the number value for the Power of Zero exponent, by working out a simple exponent Division the “Long Way”, and the “Subtract Powers Rule” way.

Image Copyright 2013 by Passy’s World of Mathematics

It can be seen from the above calculations that 2 to the power of zero equals 1.

We can also work out the numerical value of the Index Power of Zero, using patterns of Powers, as shown in the following diagram.

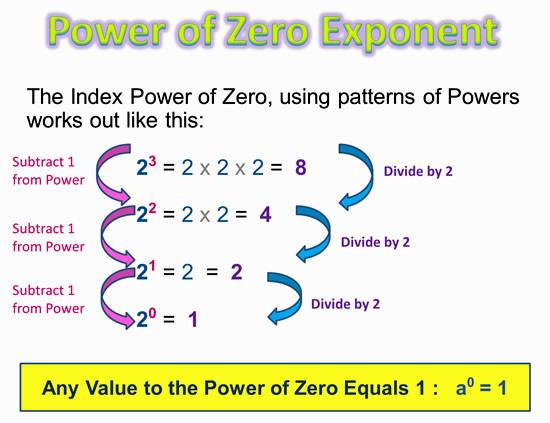
Image Copyright 2013 by Passy’s World of Mathematics

From the work we have just done here, we can be quite certain that 2 to the power of zero equals 1. In fact ANY number or letter variable to the power of zero always equals 1.

Power of Zero Examples

No matter whether the value is a fraction, a really big number, or a variable letter, the answer is always “1” when this value is raised to the Power of Zero.

However, we need to be careful about exactly which part of a multi-item expression the Power of Zero actually applies to.

This is shown in the examples below.

Image Copyright 2013 by Passy’s World of Mathematics

Negative Exponents

Negative Exponents are associated with Fractions.

We can prove this by working out a simple exponent Division the “Long Way”, and the “Subtract Powers Rule” way.

Image Copyright 2013 by Passy’s World of Mathematics

Like we did with the Power of Zero Exponent, we can also do the Negative Exponent proof using Exponent Patterns.

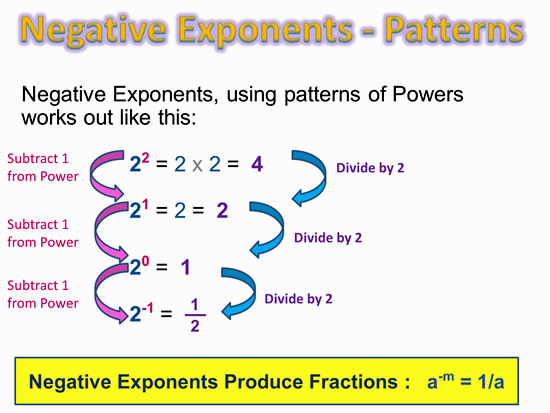
Image Copyright 2013 by Passy’s World of Mathematics

Negative Exponent Rule

Image Copyright 2013 by Passy’s World of Mathematics

When we have a negative exponent on an item, we move it down to the bottom of the fraction, where it it then becomes a positive exponent power.

Negative Exponents – Examples

Shown below are some simple, and then some more complicated examples of how we simplify Negative Exponents by creating Fractions that have all of their exponent powers positive.

An expression is not fully simplified until all of its Negative Powers have been converted into Fraction Positive Powers.

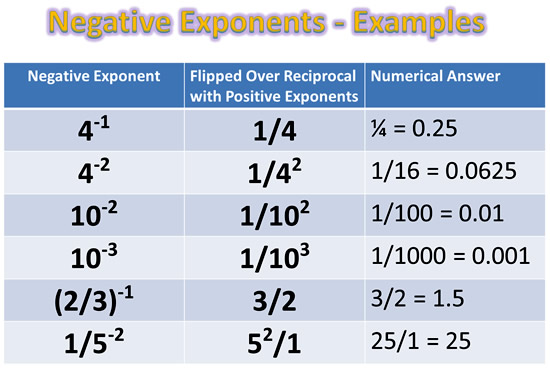
Image Copyright 2013 by Passy’s World of Mathematics

The last two examples in the above table are a little more involved than the 1/ fraction types.

We need to look at the “full story” on negative exponents and reciprocals.

The “Reciprocal” of a Number is the 1/ fraction of that number.

The “Reciprocal” of a Letter variable is the 1/ fraction of that letter variable.

The “Reciprocal” of a Fraction is the fraction flipped over so it is upside down – eg. 2/3 becomes 3/2.

Negative Exponents – “The Full Story”

The complete approach to dealing with all Negative Exponents is as follows:

Image Copyright 2013 by Passy’s World of Mathematics

The Power of Power Rule, (as well as the Expanding Products and Quotients Rules), can also be used when we have Negative Exponents present.

Just remember: An expression is not fully simplified until all of its Negative Powers have been converted into Fraction Positive Powers.

Eg. There should never be any Negative Exponents left hanging around in our Answers.

Image Copyright 2013 by Passy’s World of Mathematics

Videos About Zero and Negative Exponents

The following is a good Introductory Video on the basics of Negative Exponents.

This next video revises dividing exponents and then moves on to creating zero exponent and negative exponents.

It provides very good explanations, and shows plenty of examples, so is well worth watching.

The following Khan Academy video explains how zero and negative exponents arise from the patterns that are formed by powers.

Negative Exponents as “Opposites”

Another approach, which leads to the exact same situations we have covered up to now, is to use the idea of OPPOSITES.

With Positive Exponents we multiply the Base out as many times as the power number says to.

Negative is the OPPOSITE of Positive.

Division is the opposite of Multiplication.

This leads to the following Negative Exponents Rule:

FOR NEGATIVE EXPONENTS WE DIVIDE THE BASE AS MANY TIMES AS THE POWER NUMBER TELLS US TO.

Some people find this an easier way to deal with Negative Exponents.

The following thirteen minute video shows how Negative (Divide) Exponents are the Opposite of Positive (Multiply) Exponents.

It has a very detailed explanation, followed by several examples.

Related Items

Indices and Exponents in the Real World
Basic Indices and Exponents
Multiplying Exponents
Dividing Algebra Expressions
Dividing Exponents Using Subtraction Rule
Power of Power Exponents Rule
Expanding Exponent Products
Expanding Exponent Quotients

Subscribe

If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.

Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.

To find out exactly how free subscription works, click the following link:

How Free Subscription Works

If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.

If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:

Please state in your email that you wish to obtain the free subscriber copy of the “Zero and Negative Exponents” Powerpoint.

Help Passy’s World Grow

Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.

Help us to maintain this free service and keep it growing.

Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!

PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.

Enjoy,
Passy