
Copyright Image Purchased by Passy’s World from Dreamstime.com
In this lesson we look at some of the Mathematics associated with Surfing.
We cover the Mathematics of Ocean Waves, as well as the physics associated with catching and riding a surfable wave.
A knowledge of Mathematics is not required to be a surfer; however the mathematics of waves is used for designing artificial surfing reefs, computer wave modelling for testing ship designs, bridges, and coastal construction, and for converting wave energy into electricity.
In later lessons we look at the Geometry of Surfboards, as well as the Generation of Electricity from Sea Waves.
What Causes Water Waves

Image Source: http://www.culut.com
When wind blows over the vast expanses of open water, it transfers energy to the water surface and creates water waves.
Three factors influence how big these waves are:
– the speed of the wind
– the distance the wind travels over the water, which is called the “fetch”
– the length of time the waves travel for
The amount of energy imparted from Wind to Water is highly efficient, being proportional to the fourth power of wind speed!
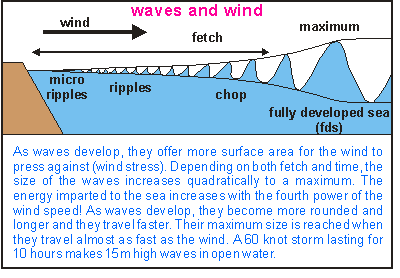
Image Source: http://www.seafriends.org.nz
The biggest surf waves are created by storms a long way from shore, out in the open ocean.
These storms are caused by low pressure to high pressure gradient differences, like the gradients that exist between cold air in Alaska and warm Pacific Ocean Air.
Storm waves start out as huge, choppy waves, and then gradually join together into strong, smooth separated lines of peaks called “swell”.
Large waves with the most energy are formed by strong wind blowing over a long period of time over a long distance (or “fetch”).
Eg. Wave Energy = Wind Speed x Wind Duration x Fetch Distance
These waves will evolve into lines of long waves (called “swell”), which has a long “Period” time between successive waves, so that breaking waves will not interfere with each other.
These longer period waves also travel faster, resulting in them producing greater kinetic energy when they eventually reach a shoreline and break.
These waves also have their energy extending deeper below the surface of the water, resulting in a bigger wave pushing up at the shoreline which has greater refraction bending which further focuses its energy.
Predicting Large Waves
There is an extensive system of open Ocean Buoys which continuosly collect data about how high waves are, (the “Amplitude”), and how long it is between successive waves (called “The Period”).
The buoy system is used for Tsunami monitoring, and also by maritime agencies to alert rough storm sea conditions to ships at sea.
However Surfers also use the publicly available data to predict when powerful waves will reach big wave surf spots such as “Mavericks” in Northern California.
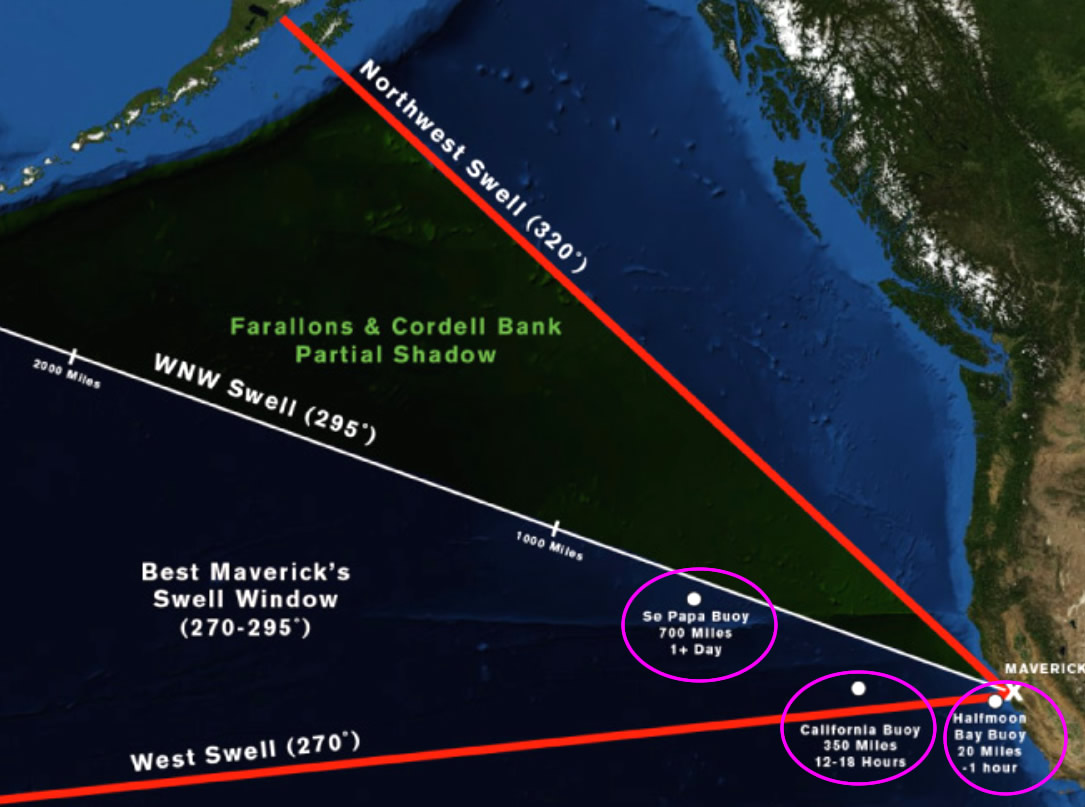
Image Source: Mechanics of Mavericks at http://www.surfline.com
Click the above image to view full size.
Here is a graph produced from ocean buoy measurements of one of the largest storm swells to ever reach the “Mavericks” surf break in California.
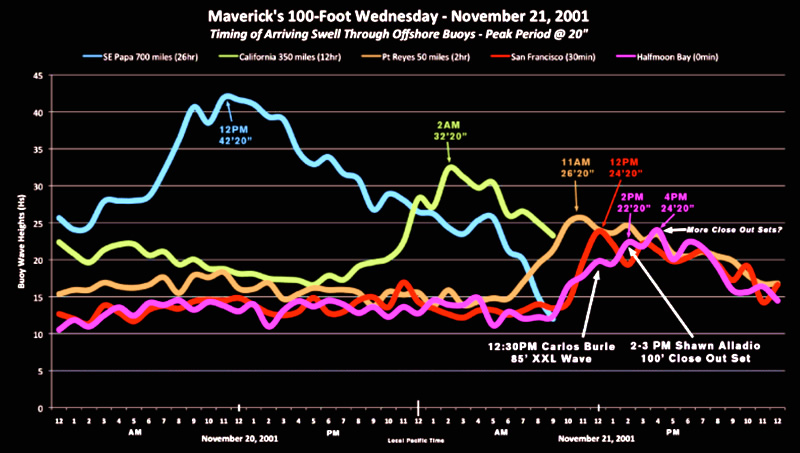
Image Source: Mechanics of Mavericks at http://www.surfline.com
Click the above image to view full size.
Breaking Waves

Image Source: Bells Beach from magicseaweed.com
The shape of the ocean floor and the direction of the wind are the two main factors that cause how a wave breaks or crashes against the shoreline.
The best surfing waves are usually caused by underwater features like sand banks, rocky points or reefs.
To get the hollow tubes that surfers love, the ocean floor needs to have a steep underwater slope.
Waves tend to break more gently and farther out if the slope of the ocean floor is gradual.
When the wind blows from the beach out to the sea, it is called “Offshore” and helps to maintain clean glassy waves, which are better to surf.
When the wind blows from the ocean to the beach (“Onshore”), or across the beach (“Cross-Shore”), it makes the waves messy and choppy.
The key mathematical measurements made on Surf Waves are the following:
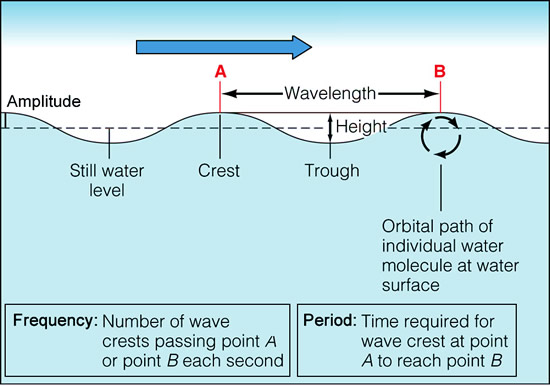
Original Image Source: http://science.kennesaw.edu
In water waves, the energy travels but the water does not.
The water particles move in small circular motions as each wave passes by.

Image Source: http://bc.outcrop.org
The size of the circular motion decreases as we get deeper below the wave, and dies out at a depth that is equal to half the wavelength.
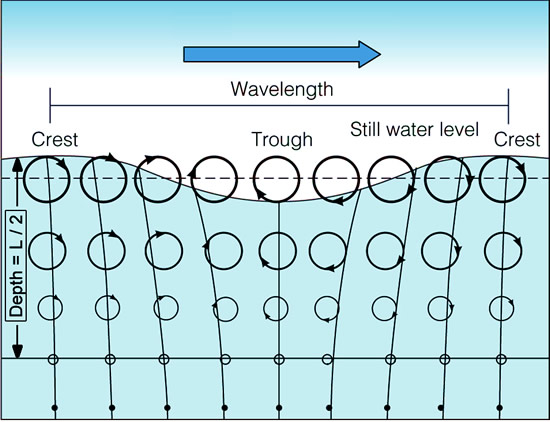
Original Image Source: http://science.kennesaw.edu
As shown in the previous diagram, the Energy in the wave is stored between the top of the wave and a depth which is about one half the wavelength.
When the water depth decreases to be come about half the wavelength, then the wave becomes what is known as a “Shallow Water Wave”.
As the water becomes shallower, the wave rises up, it becomes higher, and eventually its potential energy is converted into kinetic energy and we get a breaking wave.
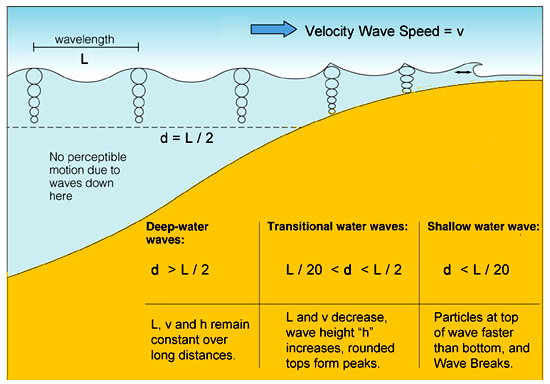
Original Image Source: http://science.kennesaw.edu
Note that in our diagram, we have referred to the speed of the wave as “v”.
However, in most diagrams the speed variable is labelled as “c” for “Celerity” which is the term oceanographers use to refer to wave speed.
Water Wave Equations
As per our previous diagram, there are three main types of incoming wave:
– Deep Water where Depth > L / 2
– Transitional where L / 20 < Depth < L / 2
– Shallow where Depth < L / 20
The shape of water waves is not actually Sinusoidal, it is Trochoidal.
A "Trochoid" can be defined as the curve traced out by a point on a circle as the circle is rolled along a line.
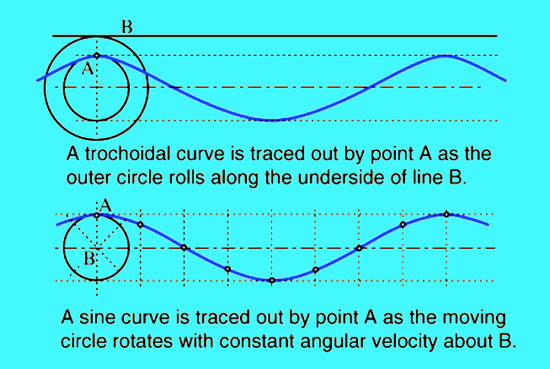
Original Source: http://hyperphysics.phy-astr.gsu.edu
The Trochoid shape does approach the sine curve in shape for small amplitudes, found in Deep Water Waves.
However at Transitional water depth the shape is different, with a narrowing of the peaks of the trochoid compared to the sinusoid.
This narrowing or steepening of the peak becomes more pronounced as the wave amplitude increases, as the wave starts to rear up and break.
The Trochoidal shape can be approximated to the shape of the Hyperbolic Tan Function graph, tanh(x) which is shown below.
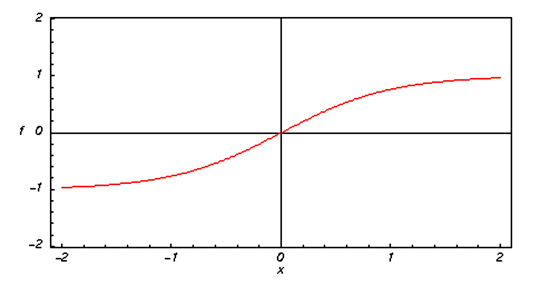
Image Source: http://functions.wolfram.com
As a result of the wave shape change from approximately sinusoidal, to trochoidal as a wave approaches the shoreline, we end up with three different Wave Speed Formulas, for out three differing water depth wave types.
The Speeds of these three wave types have the formulas shown below, where the Speed is assigned the oceanographer’s name of “c” for “Celerity”.
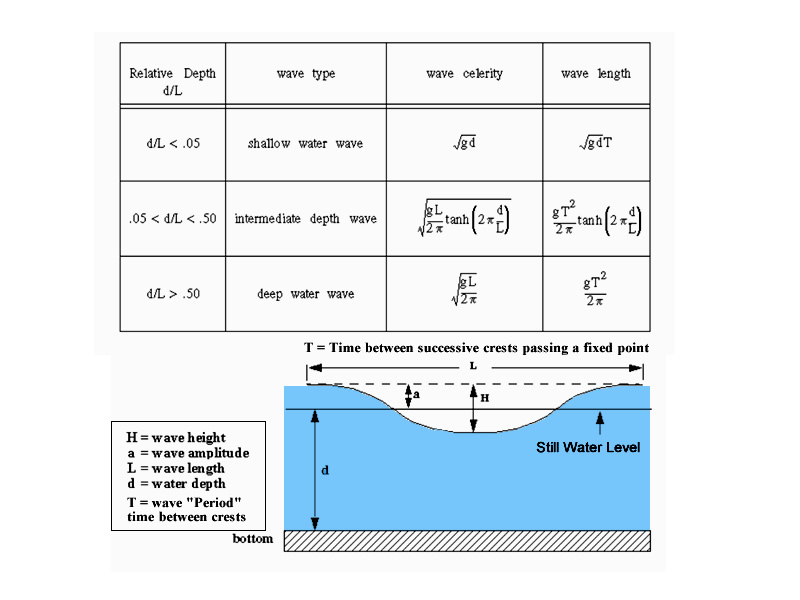
Original Image Source: http://scubageek.com
Click the above figure to view as enlarged on a separate screen.
Some things to note about these equations are the following:
1) In Deep Water the celerity, (or speed), is independent of water depth, because deep water waves do not interact with the sea bottom. Hence there is no “d” in the Deep Water equations. Their speed is a function of Wavelength, and their wavelength remains constant in the open ocean due to the dispersive nature of water.
2) Shallow water surface waves, on the other hand, do feel the bottom, and slow down as the square root of the water depth. Their speed is not a function of the wave length, but a function of water depth, and the earth’s gravitational force constant.
3) The Wave Period “T” is independent of the water depth. The time between successive crests of waves (The Period “T”) remains constant, irrespective of depth. (See “Constancy of Wave Period” in references below, for more information).
As a result of this constant “T”, in deep water, the wave length is constant, but as waves approach a beach the wave length decreases as the square root of the depth.
4) Tsunami waves behave like shallow water waves, after they break they surge forth (often for long distances), and then recede again back out into the ocean.
Information from the “Scuba Geek” site relating to Tsunamis is as follows:
“Wind-generated waves typically have periods from 1 to 25 seconds, wave lengths from 1 to 1000 meters, speeds from 1 to 40 m/s, and heights less than 3 meters. Seismic waves, or tsunamis, have periods typically from 10 minutes to one hour, wave lengths of several hundreds of kilometers, and mid-ocean heights usually less than half a meter. Because of their long wavelengths, tsunamis often satisfy the criterion for shallow-water waves. For example, when a tsunami with a wave length of 200 km passes over a depth of 4 km (the average depth of the oceans) the relative depth is d/L=.02. Since this is less than .05, this tsunami is a “shallow-water wave”, and its celerity depends only on the water depth.”
5) The Three Zone Water Wave Equations as presented above, represent a simplified overview of real world wave behaviour, compared with the water wave equations used in computer modelling of waves. (We look at Computer Modelling in the next section).
If you need to find out more details and derivations of these equations, click the links below:
Click here for Constancy of Wave Period Proof
http://hyperphysics.phy-astr.gsu.edu/hbase/waves/watwav2.html
http://scubageek.com/articles/wwwceler.html
http://functions.wolfram.com/ElementaryFunctions/Tanh/introductions/Tanh/ShowAll.html
Computer Modelling Waves
Image Source: http://www.aquaveo.com
Computer Modelling of Waves can be used as part of designing breakwaters, marinas, light houses, oil rigs, ships, tourist resorts, water fun parks, and artificial surfing reefs.
If you are in need of a massive amount of water wave Mathematics and Equations, then work your way through the US Army Corps of Engineers Coastal Engineering Manual.
This manual goes into water wave equations in full depth.
The full set of equations for water waves are quite complex, but the good news is that the equations can be programmed into a computer, and then combined with statistics and grid meshing methods to create an interactive water wave model.
The equations only need to be put into the program once, and from there onwards it is simply using the Computer App to adjust variable values and perform investigations.
The type of equations which can be programmed into a computer to do very realistic simulation exercises for Water Waves involves the the RCPWAVE Model:
Here are the definitions of the Terms and Variables found in the RCPWAVE Model Equations:

Image Source: US Army Coastal Engineering Manual
Some of the mathematical equations used in the RCPWAVE model are shown below.

Image Source: US Army Coastal Engineering Manual
The above material is from Chapter 3 of the US Army Coastal Engineering Manual.
If you would like to examine a full copy of the entire manual, then click the link below:
http://140.194.76.129/publications/eng-manuals/
Effect of Sea Floor

Image Source: Mechanics of Mavericks at http://www.surfline.com
The shape of the Ocean floor (called “bathymetry”) plays a very big part in whether or not breaking surf waves will form.
Eg. There can be large surf waves at one beach, and then around the point at the next cove, there are not any surfable waves of any reasonable size.
The ocean floor needs to rise up suddenly in the form of a rocky or coral reef, or a sandbar, for surf waves to form.
These reefs and bars create a focus point where waves are produced.
A few places around the world have perfect reef conditions for very big waves to form.
One such place is “Mavericks” in Northern California, where breaking waves can be up to four building storeys high!
Here is a short two and a half minute video showing the huge waves at Mavericks.
[youtube=http://www.youtube.com/watch?v=KMlZM9kDpMc&w=550&h=309]
Multibeam sonar can be used to map the sea floor, and at places such as Mavericks in California, it shows that we also get refraction which further focuses the wave energy, resulting in a very large wave forming at a certain location.
The refraction or bending happens because the part of the wave which hits the reef first slows down a bit, while the other part of the wave still in deeper water keeps going at a faster speed, which causes bending of the wave.
The sea floor at Mavericks has grooves cut into the steep reef, made by icebergs grinding the surface during the last ice age, as well as a fault line which runs through the reef. These grooves also channel the water and add to the power of the wave.
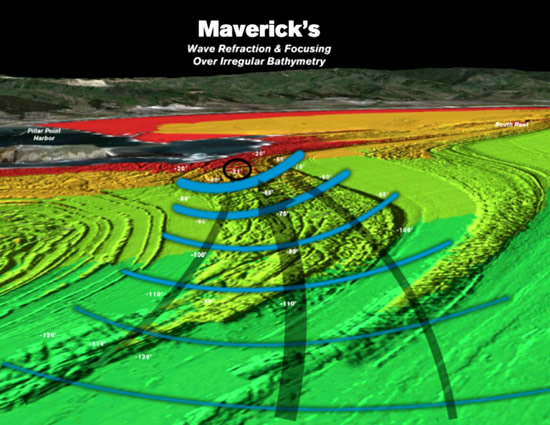
Image Source: Mechanics of Mavericks at http://www.surfline.com
There is a great slideshow presentation on Mavericks to watch at the following link.
Note that an advertisement runs on the page while the slideshow loads.
http://www.surfline.com/surf-news/mechanics-of-mavericks_62313/
The slideshow includes information about ocean buoys to measure sea and storm swells for shipping, and the data from these is used by surfers to figure out when a big swell is going to hit Mavericks.
There is a great slide about this in Part 2 of the “Mechanics of Mavericks” slideshow at the following link:
http://www.surfline.com/surf-news/-mavericks-part-two-epic-swells_62537/
The following YouTube video discusses the mathematics and science of the big waves found at Mavericks in California.
[youtube=http://www.youtube.com/watch?v=fP1QK0XCt1U&w=550&h=413]
Surfing and Tides

Image Source: http://photo.stellav.ru
Tides change the water depth, and so the bathymetry at a particular surf break varies over the tidal period.
The sea floor shape may be perfect at high tide and produces fabulous waves, but at low tide the waves are breaking on a different part of the sea bed which produces unsurfable dumper waves.

Image Source: http://www.ozcoasts.gov.au
Tides, which occur from varying gravitational forces between the sun, moon, and the earth, are easy to predict far in advance.
Surfers use Tide Charts to know when various tide conditions producing the best waves are going to occur at their favorite breaks.
Here is a sample Tide Chart for guests at the “Blue Oasis Club” Resort in Bali

Image Source: http://www.blueoasisbeachclub.com
Click the above image to view full size.
The effect of tides on wave quality differs between surf breaks.
Some breaks can be excellent on a low tide, but can suffer from a drastic drop in wave quality during a high tide, during which the water depth is too great, causing the wave face to break more slowly and with less power.
Other surf breaks may experience the opposite effect and have better wave shape during high tide.
Bathymetry, coastal geography, full moons, and man-made coastal features such as seawalls, harbors, piers, and dredging all impact how a surf break will respond to tides.
Parts of a Breaking Wave

Original Image Purchased from Dreamstime.com
The ideal place to catch a wave is in the “Impact Zone”.
The best place to surf along the wave is in the Shoulder’s clean and smooth face; however it is sometimes necessary to turn into the whitewater occasionally to pick up some more power.
Moving up and down the wave also allows gravitational potential energy conversion to kinetic energy of movement.
The surfer also needs to have a standing position which maintains their centre of gravity in balance.
Catching and staying on a wave is a delicate balance of a number of mathematical factors.
In the next sections we look at the Mathematics of paddling a board to “catch” a Wave, and then the potential to kinetic energy exchange as the surfer commences riding the wave.
Catching a Wave

Image Source: http://i3.mirror.co.uk
The surfer needs to catch the wave just as it is breaking, which is when it has maximum velocity (speed).
In order to catch the wave, the surfers’ momentum must be equal to the wave’s momentum.
The surfer has to start paddling as the wave approaches, and most people agree that the required number of paddle strokes to catch a wave is five strokes.
The fundamental mathematics of Surfing depends on Newton’s equations where mass times acceleration of the surfer, must be equal to the propulsive force produced by paddling, plus the “drag force” due to wave particle motion.
When you Paddle, the Forces involved are as follows:

Image Source: http://www.abc.net.au
You must produce enough acceleration to get your
speed as close as possible to the wave’s speed.
The Drag component of this equation expands out to something quite mathematically complicated, but basically the drag is an assistant force due to the circular movement of water particles in the wave, and actually gives the swimmer/surfer some extra speed.
Think of the wave drag as being like the current that helps you when you swim downstream in a river.
The end result of the Mathematics underlying the ma = P + D equation, is that the surfer must paddle fast enough to attain equal to, or a little bit less than, the actual speed the wave has.
If the swimmer or surfer does not achieve this required speed, the wave will pass by without them catching it.
There is a great five minute video featuring Professor Neville de Mestre which discusses this at the following link:
http://www.abc.net.au/catalyst/stories/2377157.htm
A much fuller detailed paper by Professor Neville de Mestre published by Austrlalian Mathematics Association is available at the following link:
http://www.austms.org.au/Publ/Gazette/2004/Sep04/demestre.pdf
Paddling Speed Equation
The Speed a Surfer needs to paddle to catch a wave is dependent on the Height of the Wave.
This is the case because larger waves have more energy and travel at higher speeds.
The following formula has been developed for the required Paddling Speed by Professor David Sandwell.
(Note that the diagram is an aerial view of waves breaking along a headland, or what surfers often refer to as a “Point Break”).
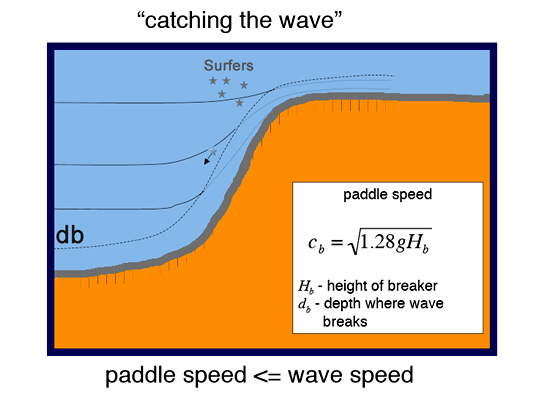
Original Image Source: http://topex.ucsd.edu
Videos About Catching Waves
The following is a great practical video about the steps to catching a wave:
[youtube=http://www.youtube.com/watch?v=hVyatMUYwZw&w=550&h=309]
This next video is all about the importance of catching a wave at the peak.
[youtube=http://www.youtube.com/watch?v=hcHWWBWdzzc&w=550&h=309]
Types of Surfing Waves
There are four main types of Wave which are associated with Surfing.
In order from smallest to largest, these are the Longboard Wave, the Fun Wave, the Tube Wave, and the Tow-In Wave.
Geometrical Shape of Tube Waves
One of the four types of Surfing waves is the “Tube Wave”. This is the classic curling wave which surfers love the best. Tube waves contain plenty of power and provide an exciting ride, especially if you can get yourself inside the tube of water.
Being inside a tube is awesome!
It is like being transported temporarily into a calm and peaceful cylindrical crystal palace.

Image Source: http://ocean.si.edu
The only drawback is that if the “Crystal Palace” unexpectedly caves in, the weight of the seawater (at around 1kg per cubic meter), can pack a decent punch to your head!)
A Geometrical Ratio used to describe the shape of Tube Waves, that involves the measurement of the maximum width and length, as per the following diagram:
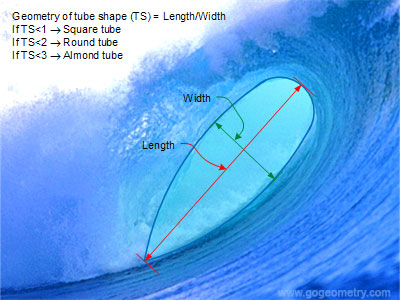
Image Source: http://www.gogeometry.com
The geometry of tube shape is represented as the ratio between Length and Width.
A perfectly cylindrical vortex has a ratio of 1:1, while the classic almond-shaped tube is nearer 3:1.
When width exceeds length, the tube is described as “square”.
Information Source: http://www.gogeometry.com
Wave Speeds of the Four Wave Types
Professor David Sandwell has determined the following relationship between Ocean Depth and Breaker Height, as well as determining Average Wave Speeds.
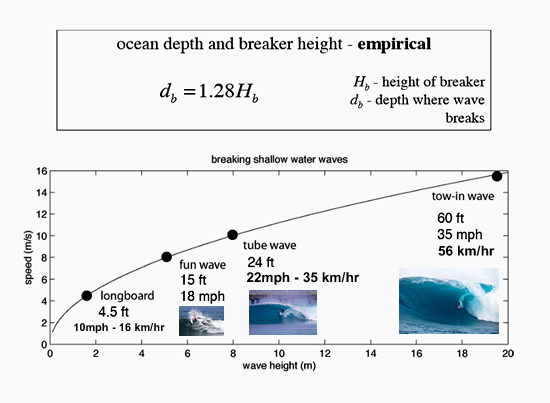
Original Image Source: http://topex.ucsd.edu
From the speeds of the bigger waves, we can see that a surfer cannot paddle fast enough to “catch” these waves, and a technique called “Dropping In” is used to generate the required additional speed.
“Dropping In” involves the conversion of Gravitational Potential Energy into Kinetic Energy by the surfer dropping down the front of the wave. This is discussed in the next section.
Dropping In
Image Source: http://www.govisitcostarica.com
“Dropping in” is a method of gaining enough speed to catch and stay on a wave that is moving too fast to catch merely by paddling as hard as possible. The drop down the wave provides the needed speed for the surfer to be able to stay with the wave.
This is the same idea as riding a bike down a really steep hill, or a skateboard down a steep ramp.
Going down a steep incline increases your speed, because you convert earth gravitational energy into moving kinetic energy.
“Dropping in” is also a term used for stealing another surfer’s wave by “Dropping In” on him.
Eg. The rules are that the surfer on the inside, closest to the “Impact Zone” and whitewater has the right of way.
In the following video two surfers drop into the same wave, but the one on the left of screen should have given way to the one on the right of screen. (via the who is on the Inside Rule).
The left guy illegally gets the wave, but then the Karma Gods catch up with him and he gets totally smashed and eaten by the wave.
[youtube=http://www.youtube.com/watch?v=S8f9HVvezMQ&w=550&h=413]
Dropping down the wave converts Potential Energy into Kinetic Energy. This Kinetic Energy can supplement paddling speed and enable catching the wave to occur.
The following calculation produces a Formula which calculates Surfer Speed at the bottom of a Wave.
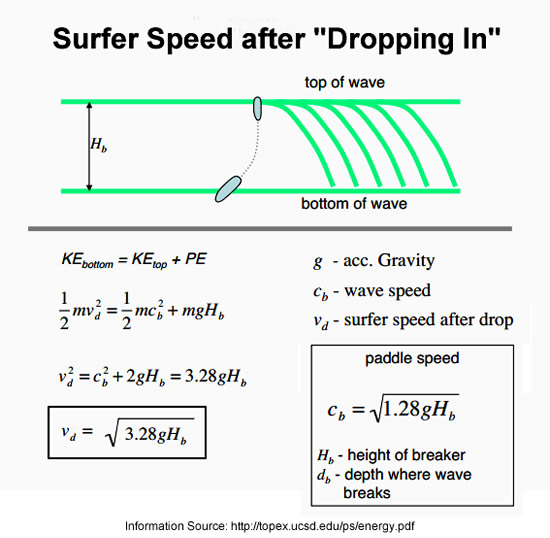
Original Image Source: http://topex.ucsd.edu/ps/energy.pdf
Substituting the typical wave heights of our four standard wave types produces the following Results:
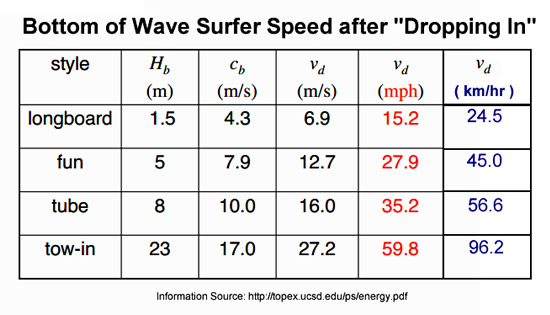
Original Image Source: http://topex.ucsd.edu/ps/energy.pdf
When a surfer “drops in” to accelerate down the face of the wave, this needs to be done at an angle across the “face” of the wave.
Anyone who has ever dropped straight down the face of a wave knows the subsequent “nose dive wipe out” crash which usually results.
The Drop In Angle can easily be calculated using our previous values of :
Initial Paddle speed “c” (which needs to match the wave speed to catch the wave),
and
Surfer’s Speed “v” at the bottom of the wave at the end of the Drop In.
As shown below, this “Cutting Across” angle ends up being a value of 50 degrees.
The wave moves forward breaking across horizontally at its moving forward speed, and we drop down the wave increasing our speed.
To stay out of the white water, and move across the wave face, we need to point at an angle of 50 degrees.
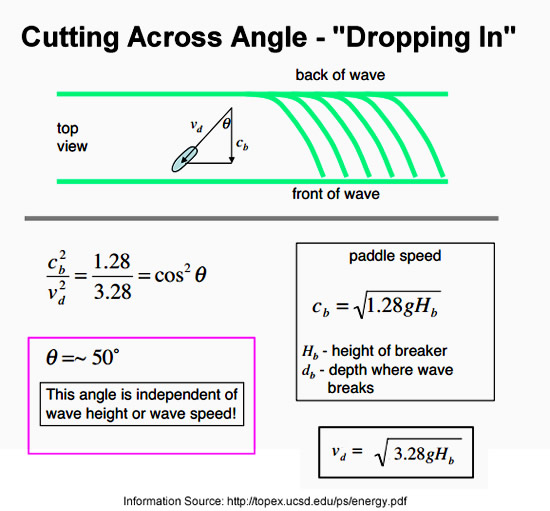
Original Image Source: http://topex.ucsd.edu/ps/energy.pdf
Note that the bulk of the diagrams in this section are modified from material supplied in David T Sandwell’s presentation titled:
“Physics of Surfing Energetics of a Surfer”. Click the link below to view his complete presentation.
http://topex.ucsd.edu/ps/energy.pdf
Surfing the Wave

Image Source: http://picasaweb.google.com
Once we have paddled at sufficient speed and / or “Dropped In” to catch the wave, we continue to use the conversion of Gravitational Potential Energy to Kinetic Energy to move along, and go up and down the wave as we do this.
Remember that our speed has to stay close to the speed of the wave, or we will not be able to keep up with it, and it will pass by underneath us.
The following three minute video shows the mathematics of Surfing the Wave in action.
[youtube=http://www.youtube.com/watch?v=O_oADJ961vo&w=550&h=413]
For the remainder of the Surfer’s ride across the wave, (after the initial “Drop In”, there are usually repeated up and down the wave travel, combined with turns and acrobatic manoeuvres, until the wave has dissipated or the surfer elects to end the ride.
For really big fast moving waves there is not enough time for a lot of up and down the wave manoeuvres, as taking the drop down the face and surviving is the surfer’s main concern.
To demonstrate this, here is a video of Shane Dorian Surfing a really big wave at “Jaws” in Hawaii.
[youtube=http://www.youtube.com/watch?v=O9crPOB_9tE&w=550&h=309]
Shane Dorian was incredible to take the Drop and catch a wave like this at Jaws. Large waves like these can be moving typically at 35 mph (60km/hr), and often it is not possible to catch them by paddling a surfboard up to your best paddling speed.
Usually Jet Skis are used to tow a surfer up to speed and into a wave of this size, especially at huge breaks like Mavericks in California, and Jaws in Hawaii.
Tow In Surfing

Image Source: http://www.offshoreodysseys.com
“Tow-In Surfing” or “Tow Surfing” is a relatively new form of Surfing that was developed by the creative efforts of Laird Hamilton and his friends in Hawaii in the early 90’s.
Tow Surfing combines Surfing with wakeboarding and waterskiing, where a person is towed behind a vessel utilizing an extension rope with a grab handle, and standing on a special Tow-In Surfboard.
Tow Surfing derived from the desire of Big Wave Surfers to be able to power surf larger waves that were breaking on outer reefs and typically incapable of catching due to their size and speed.
The size of these waves generally tracked towards land at faster rates than could be paddled into by “Guns”, surfboards designed for larger waves.
Laird and his partner’s utilized technology and background products from windsurfing, and surfing which created specialized tow boards with foot straps, and designed for stability and high speed.
A 155hp Yamaha Waverunner with a top speed of 65 mph is a popular Jet-Ski used for tow in surfing.
Speeds of up to 40 mph (60 km/hr) are required for Tow Surfing, because the huge waves that are surfed are usually traveling through the water at around 35 mph.
Here is a video showing an awesome demonstration of Tow-In Surfing.
[youtube=http://www.youtube.com/watch?v=3oS_28utt2Y&w=550&h=413]
There is a great website dedicated to Tow-In Surfing at the following link:
Surfing Statistics

Original Image Source: http://i.telegraph.co.uk
Shown above is what is currently the biggest wave believed to have ever been Surfed: a 100 ft / 31m storm wave on the coast of Portugal.
Brazilian surfer Carlos Burle rode the monster wave recently in October 2013.
The wave was created by the St Jude storm at Praia do Norte, near the fishing village of Nazare.
Estimated at possibly over 100ft, it is believed to be the biggest wave ever ridden.
Forty Five year old Hawaiian surfer Garrett McNamara also surfed a 100 foot wave at the same location in January 2013. It will not be known until around April 2014 when they decide the Surfing Year’s biggest wave winner as to who exactly is the world record holder.
The following videos show these epic wave rides.
[youtube=http://www.youtube.com/watch?v=7tAp5WFhMwM&w=550&h=309]
[youtube=http://www.youtube.com/watch?v=csothimiWjc&w=550&h=309]
[youtube=http://www.youtube.com/watch?v=k5Gb0ceZibg&w=550&h=309]
The unique bathymetry of the Nazarre Portugal region sea floor which causes these monster waves.

Image Source: http://i.ytimg.com
As per the above image there is a Huge Underwater Canyon that the water is channelled along which suddenly bottoms out near the shore. This creates monstrous waves from incoming rogue waves from big storms in the Atalantic Ocean.
Here are some other interesting Surfing Statistics
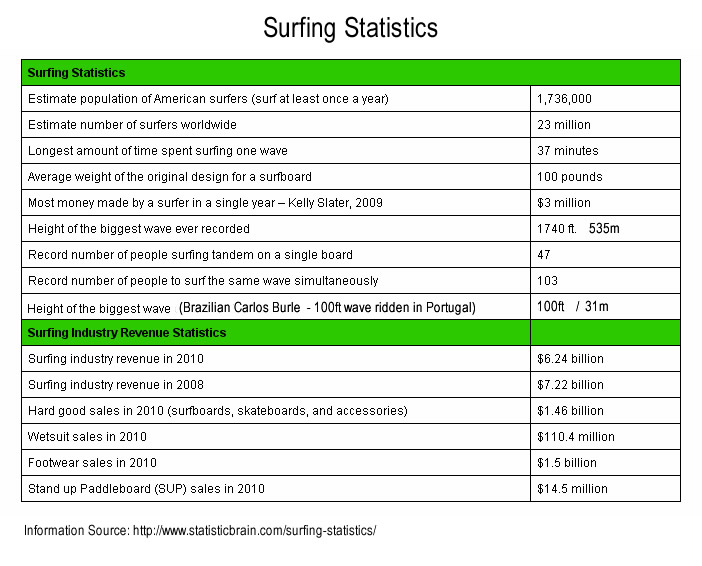
Original Image Source: http://www.statisticbrain.com
Click to Enlarge the above Image.
Note that the Biggest Wave ever recorded (1740ft / 535m) was a giant Tsunami wave which hit the coast of Alaska in 1958.
How Heavy is a Big Wave
The following video has all the answers
[youtube=http://www.youtube.com/watch?v=M9-CaewvynA&w=550&h=309]
Artifical Surf Breaks

Image Source: http://surfspotsmap.com
Australia is currently leading the way in building coastal engineering structures which prevent beach erosion, as well as supply improved surfing conditions.
Places around the world with artificial Surf Breaks include:
Narrowneck, Queensland, Australia
Cables, Western Australia, Australia
Pratte’s Reef, El Segundo, California, Los Angeles
Bagarra, Queensland, Australia
Mount Manganui, NZ
Bornemouth, UK
Kovalam, India
The current cost of building an artificial reef is between 1 and 10 million dollars.
The quest to build artificial reefs has had mixed results.
Cables in Perth used granite boulders and has withstood the test of storms, and is still surfable. It provides a reasonable surf spot in suburban Perth; however there has been controvery that it does not supply enough surfable days througout the year, and works best in winter.
In all fairness to the builders of the reef, Perth is hampered by choppy water in summer (due to Rotnest Island absorbing a lot of wave power), and strong cross shore south westerly winds.
Unlike Perth’s granite boulders, the sand bags reef in Bournemouth UK suffered substantial movement, resulting in unsafe under currents and had to be closed in 2011.
Narrowneck in Queensland has also been closed for periods of time after storm damage.
The Indian artificial reef appears to have been quite successful; however its longevity is yet to be proven.
Working in conjunction with the Indian government, ASR Ltd completed construction of India’s first Multi-Purpose Reef in February, 2010.
The primary purpose of the reef is to mitigate coastal erosion from monsoon waves in the small town of Kovalam.
The Aritifical Reef also creates an excellent habitat for marine species.
Finally, as this video shows, the reef has helped create a nice surf spot.
[youtube=http://www.youtube.com/watch?v=mGYuj-Ow1rk&w=550&h=309]
If you would like to read more about Artificial Reefs, there is a good article within this web page:
http://www.seafriends.org.nz/oceano/beacheng.htm
Continuous Wave at Waimea Bay in Hawaii
Not all Surfable waves are found in the Ocean!
Kelly Slater & locals were able to surf a river wave at Waimea Bay in January 2011 after the river flooded and broke the beach in two and created a continuous wave.
Here is a video showing their exploits:
[youtube=http://www.youtube.com/watch?v=ljVbieeFn14&w=550&h=413]
Surf Aid Mathematics Teaching Resources
Image Screen Captured from Surf Aid Website
Surf Aid is a not for profit organisation sponsored by Billabong with a kean interest in the preservation of Mentawai in Indonesia.
The Mentawai Islands are a chain of about seventy islands and islets off the western coast of Sumatra in Indonesia.
It is totally free to join the “Surfaid Schools Program”, and all that is required is submission of your email address.
http://www.surfaidinternational.org/schoolsprogram
Downloadable Free Units which are in ZIP and PDF format which could be of use to Mathematics Teachers are the following:
AUS Maths 12-14
Mathematics – Connections through Surfing
Technology
Destination Mentawai Islands
The Economics Of Aid
Crossing The Divide – Primary
These are all free PDF and ZIP file downloads
A Typical example might be the following questions about traveling to surfing locations on various Islands:
“If the motor launch can manage an average speed of 15knots, calculate the journey time between each
location. 1knot is 1 nautical mile per hour. You can assume there is sufficient sailing staff to keep moving 24 hours per day. Round up your answers to the nearest day and complete worksheet 5.3.
If you move 10º around the equator how many nautical miles have you traveled?
What angle around the equator (change in longitude) corresponds to 1 nautical mile?”
Another activity we looked at was all about “Planning an Overseas Surfing Trip”.
Eg. Costs, Savings Plan, Items needed and their Cost, and so on.
It was very surfing orientated and might alienate non-surfers and female students, but could easily be adapted to be a group of friends planning a Bali Holiday, and undertaking various tours and activities whilst in Bali.
We will be going through all of the Surfaid Materials, and seeing what could be incorporated into some middle school mathematics, even though the school Passy works at has a tiny minority of students who have ever been Surfing.
We suggest you could easily do the same for your classes.
AMC Mathematics Teaching Resources
The Australian Maritime College has an excellent set of free resources for Mathematics Teachers.
Among these is a very good mathematical exercise about Wave Refraction.
Go to the following link to find their Resources page:
http://www.amc.edu.au/why-study-maths
To get the workbooks and other resources, it is necessary to register your school and complete an order form online.
These resources are free to Australian schools, and if you would like to see what some of the workbook exercises look like, then check out the following link:
Click here for AMC Online Maths Workbook PDF
The AMC is planning to add more online interactive lessons, but as of late 2013 the current the interactive lessons are as follows:
A Study of Similar Vessels (an application of Curve Fitting) – 5mins
Wind Farm Feasibility Study (an application of Probability) – 12mins
Vessel Speeds in Waves (an application of Differentiation) – 5mins
Ship Hydrostatics (an application of Integration) – 12mins
Wave Refraction (an application of Trigonometry) – 12mins
Ocean Waves (an application of Superposition) – 5mins
Scaling Laws (an application of Algebra) – 8mins
The AMC can be contacted about this program at the following email address: whystudymaths@amc.edu.au
Further Reading / References
The following is a list of stand out resources which we found on the Internet while researching this lesson.
Mechanics of Mavericks
http://www.surfline.com/surf-news/mechanics-of-mavericks_62313/
http://www.surfline.com/surf-news/-mavericks-part-two-epic-swells_62537/
Physics and Energy of a Surfer – David T Sandwell
http://topex.ucsd.edu/ps/energy.pdf
Speed of Ocean Waves
http://hyperphysics.phy-astr.gsu.edu/hbase/waves/watwav2.html
Near-shore swell Estimation from a Global Wind-Wave Model
http://www98.griffith.edu.au/dspace/bitstream/handle/10072/17987/49454_1.pdf
US Army Corps of Engineers Coastal Engineering Manual
http://chl.erdc.usace.army.mil/cem
http://140.194.76.129/publications/eng-manuals/
http://www.marine.tmd.go.th/Part-II-Chap1.pdf
Artificial Surf Reefs
http://www.coastalmanagement.com.au/artificial-surfing-reefs/
http://www.surfingramps.com.au/CablesArtificialSurfingReef.htm
http://en.wikipedia.org/wiki/Multi-purpose_reef
http://www.surfscience.com/topics/waves-and-weather/wind-and-weather/artificial-surfing-reefs/
Other Surfing Topics
http://www.kidzworld.com/article/6839-the-science-of-surfing#ixzz2krLEbzMg
http://www.seafriends.org.nz/oceano/waves.htm
http://www.gogeometry.com/wonder_world/surfing_tube_ride_shape_golden_rectangle.htm
Maths and Science Teacher Resources
http://www.surfaidschools.org/
http://www.surfaidinternational.org/schoolsprogram
About the Author

Image Copyright 2013 by Passy’s World of Mathematics
I have been a keen Surfer for over 20 years, and have surfed all along the East Coast of Australia, all around Indonesia, as well as visiting Fiji and Hawaii.
I was sidelined from serious surfboard Surfing around 6 years ago after a spine operation to repair cumulative damage caused by Surfing and Bike Riding accidents. However I still body surf and boogie board surf whenever I can.
My son is a keen body boarder, and that is him first learning to surf in the bottom right hand corner photo.
MAV Conference PowerPoint
To download the PowerPoint Presentation from the Mathematics Association of Victoria Conference, click the link below and save the file to your computer.
Mathematics of Ocean Waves and Surfing
Click the link below to download this 12MB PPT File:
http://passyworldofmathematics.com/MAVconfPPTs/IntroWavesSurfPPTv4.pptx
Related Items
Ocean Mathematics – Overview
Surfboard Geometry and Design
Tsunami Mathematics
Wave Power Mathematics
Shark Mathematics
Mathematics of Ships at Sea
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Like Us on Facebook
Our Facebook page has many additional items which are not posted to this website.
These include items of mathematical interest, funny math pictures and cartoons, as well as occasional glimpses into the personal life of “Passy”.
Check it out at the following link:
https://www.facebook.com/PassysWorldOfMathematics
While you are there, LIKE the page so you can receive our FB updates to your Facebook News Feed.
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy







Pingback: Surfboard Geometry and Design | Passy's World of Mathematics
Pingback: Mathematics of Ships at Sea | Passy's WordPress Test Blog
Pingback: Mathematics of Ships at Sea | Passy's World of Mathematics
Pingback: Ocean Mathematics | Passy's WordPress Test Blog
Pingback: Ocean Mathematics | Passy's World of Mathematics
Pingback: Wave Power Mathematics | Passy's World of Mathematics