
Image Copyright 2012 by Passy’s World of Mathematics
The Sydney Harbour bridge is a magnificent structure of mathematical genius, located in what has to be the world’s most beautiful city.
In this lesson we look at the mathematics associated with the Sydney Bridge, including deriving the Quadratic Equations for both the lower and upper parabolic arches of the bridge. We then look at some additional mathematics of the bridge, as well as some similar bridges in other countries.
There is an accompanying worksheet of our labelled measurement photographs, for teachers to set their own mathematics classes the task of calculating these equations. (See the “Free Gift to Subscribers” section at the end of this lesson for details).
Lower Arch Parabola
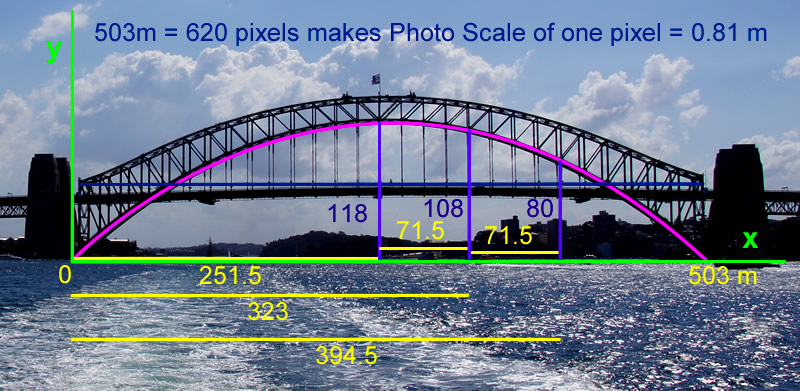
Image Copyright 2012 by Passy’s World of Mathematics
(Click the above image to enlarge to full size)
Our approach to this problem was to use a photo we had taken of the bridge, and by making measurements on the photo in pixel units, (using Adobe Fireworks), scale the photo and obtain some (x,y) values to work with.
The “Scale Factor” was derived by knowing that the real life span distance of the roadway below the arch was 503 meters, and then comparing this with the number of pixels (or dots) on the photo for this span.
As shown above, this enabled us to then establish the following key values:
Vertex Turning point is located at (h,k) = (251.5, 118)
Three other (x,y) points on the arch are: (323,108) and (394.5,80) and (503,0).
For any inverted Parabola graph, there is a standard equation that uses the (h,k) vertex, and the “Dilation Factor” of “a”, to determine the value of any (x,y) point on the Parabola graph.
The “Dilation Factor” value relates to how much the standard y = x squared parabola shape has been stretched or compressed.
This standard quadratic equation is as follows:

Image Copyright 2012 by Passy’s World of Mathematics
For the Bridge, we have the vertex value, and we have some (x,y) values, and so all we need to do is determine the “a” Dilation Factor value.
This can be done as shown below:

Image Copyright 2012 by Passy’s World of Mathematics
Substituting back into the standard equation, we then have the equation for the lower arch of the Bridge as the following:

Image Copyright 2012 by Passy’s World of Mathematics
Note that we have rounded off the Dilation Factor (“a” value) in our Equation to be 0.00188. This means in subsequent checking activities which follow, we did have to round off or truncate some “Y” values.
For better accuracy, the exact value of a = 0.001880501 can be used.
We checked the above equation, by substituting the (x,y) values (323,108) and (394.5,80) and found that the equation is true in both cases.
As a final visual check, we graphed our equation using the free online software at “Rechner Online”, and found that the graph shape does match that of the bridge.
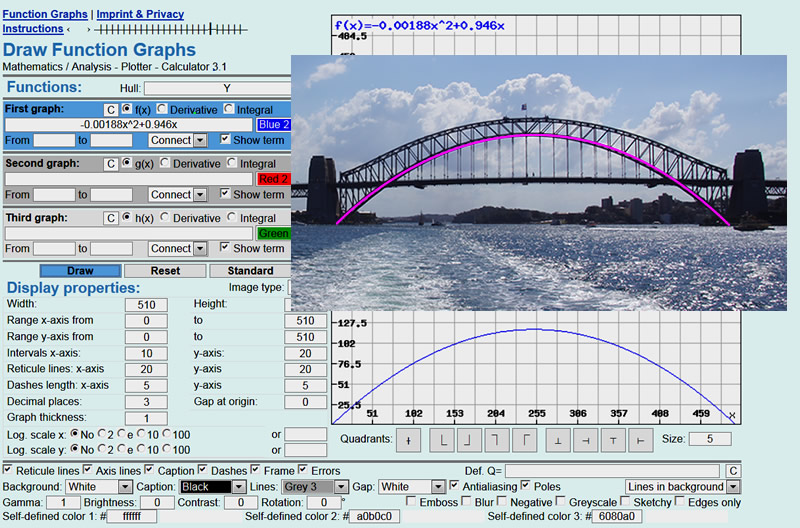
Image Copyright 2012 by Passy’s World of Mathematics
(Click the above image to enlarge to full size)
Note that we did have to transform the equation into the graphing form equation shown on the screen capture above, by fully expanding the turning point form, which cancelled out the 118.
We then superimposed our bridge photo over this graph, which confirmed we have a perfect fit:

Image Copyright 2012 by Passy’s World of Mathematics
Upper Arch Parabola

Image Copyright 2012 by Passy’s World of Mathematics
The Upper Arch of the Sydney Harbour bridge is a flatter parabola than the lower arch. The Upper Arch is a Parabola in the main section, but then curves in a reverse parabolic shape towards its two end sections.
Shown below are our pixel to meter converted measurements for the upper arch.
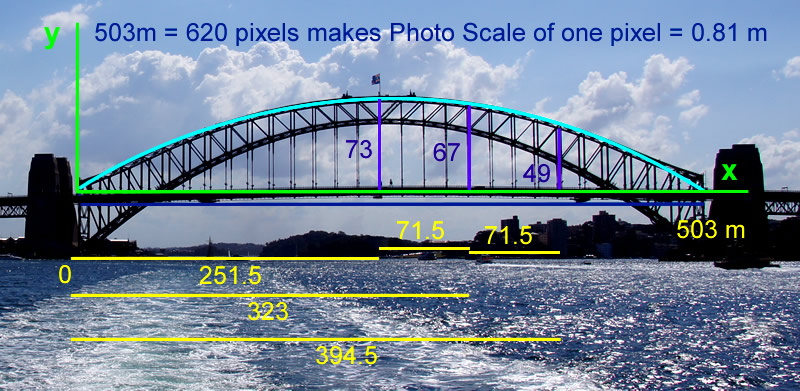
Image Copyright 2012 by Passy’s World of Mathematics
(Click the above image to enlarge to full size)
Using the same mathematical methods as we applied to the lower arch, we have determined the equation of the upper arch as follows.

Image Copyright 2012 by Passy’s World of Mathematics
Strength of the Harbour Bridge
The parabolic shape and hanging roadway gives uniform distribution of the massive weight of the bridge.
The bridge also has extensive triangulation to give it rigidity and strength.

Image Copyright 2012 by Passy’s World of Mathematics
In the cross members of the Bridge, there is also triangulation within the side beams of the main triangles. This creates maximum strength while minimizing weight.

Image Copyright 2012 by Passy’s World of Mathematics
Even under the bridge, and all the way along the sides, there is continual triangulation of the structure.

Image Copyright 2012 by Passy’s World of Mathematics
Bridge Facts and Figures

Image Copyright 2012 by Passy’s World of Mathematics
The following websites have some great photos of the bridge being built in the 1930’s, as well as plenty of mathematical facts and figures.
For example, the surface area that requires painting is equal to about the surface area of 60 sports fields.
During the building of the bridge, 272,000 litres of paint were required to give the Bridge its initial three coats. This would be enough paint to paint around 50,000 bedrooms!
On hot and cold days the two main arches may rise or fall 18 centimetres due to heating or cooling. There are hinges built on the bases of the bridge to cope with this.
http://www.pylonlookout.com.au/facts.htm
http://www.sydneyharbourbridge.info/
http://en.wikipedia.org/wiki/Sydney_Harbour_Bridge
Building of the Bridge
A brilliant Engineer called Dr Bradfield designed and project managed the build of the Sydney Harbour Bridge. Not only did he champion its concept and funding, he saw the “Hell Gate” Railway Bridge in New York in the 1920’s (completed in 1916 and almost identical in design to the Sydney Harbour Bridge though smaller) and quickly changed the specification to create a similar design for Sydney.
Had he not done so, the previously accepted design would have been built, which was quite ugly, and a very ordinary suspension bridge in comparison to the marvel we have today.
The following is a great historical video of the building of the bridge.
During the bridge construction, each half arch was held back by a series of cables anchored in tunnels carved in the rock.
There were 128 cables on the southern shore supporting the southern arch and 128 on the northern shore.
Read more about these cables and do some mathematics on the forces they contended with at the following link:
http://sydney-harbour-bridge.bos.nsw.edu.au/engineering-studies/support-cables.php
There is also some interesting engineering mathematics about Bridge Load and Reactions at the following link:
http://sydney-harbour-bridge.bos.nsw.edu.au/engineering-studies/bridge-supports.php
Locating the Bridge Pylons

Image Copyright 2012 by Passy’s World of Mathematics
“One of the most critical tasks carried out before construction began was the survey that determined exactly where each of the main bearings was to be located. This was carried out using surveying equipment and a process of triangulation from a set baseline. The survey, using a theodolite, was based on set survey marks at Mrs Macquarie’s point (G), in the grounds of Government House (A, B, E and F), on Kirribilli Head (H) and in Lavender Bay (J).
The triangulation process allowed the centreline of the proposed Bridge (C, D) to be located precisely, and from there the position of the main bearings was set.
In fact two different surveys were carried out, one by Dorman, Long & Co. Ltd. surveyors and the other by NSW Public Works Department surveyors. Each survey had its own baseline (AB and FE) and the resulting measurements were averaged to ensure a high level of accuracy.”
Read more by clicking the link below.
http://sydney-harbour-bridge.bos.nsw.edu.au/engineering-studies/engineering-surveying.php
Other Sydney Style Bridges

Image Copyright 2012 by Passy’s World of Mathematics
Imagine the shock Passy got two years ago while on top of the Empire State Building in New York City. There he spotted the above sight of the pink bridge which looked identical to the Sydney Harbour Bridge!
This New York bridge is a rail bridge called the “Hell Gate Bridge”, which was built before the Sydney Bridge. It is in fact this railway bridge which inspired Dr Bradfield’s design of the Sydney bridge.
The Sydney Harbour Bridge is 60% larger than Hell Gate.
Although not the longest arch span in the world, Sydney’s weight, width, and load capacity are greater than the world’s other major arch bridges.
Sydney Bridge was designed more than 85 years ago but has still not reached its maximum loading capacity.
The Bayonne Bridge is another steel through arch bridge in the USA, which connects New York state to New Jersey

Image Source: http://www.plansmartnj.org
It also resembles the Sydney Harbour Bridge, but was built after Sydney, and is longer and narrower than the Sydney Bridge.
The Runcorn Bridge in the UK was built in the early nineteen sixties, and is also a Sydney look-a-like steel through arch bridge.

Image Source: http://www.allertonoak.com
The Tyne Bridge (also in the UK) is a lot like the Sydney Harbour Bridge, but not nearly as big.

Image Source: http://danny.oz.au
It is erroneously thought by many people that the Sydney Harbour Bridge was a copy of the Tyne Bridge.
Information from the UK’s BBC website confirms that the much smaller Tyne Bridge was actually copied off the Sydney Harbour Bridge.
“Sydney was first to start work on its bridge and provided the template for the Tyne Bridge.
The Tyne Bridge was designed by Mott, Hay and Anderson who based their design on the Sydney Harbour Bridge.
This in turn was derived its design from the Hell Gate Bridge in New York.
It’s long been thought that the Sydney Harbour Bridge in Australia was based on the Tyne Bridge.
This is not the case and a quick look at the dates proves the case.
Work started on the Sydney Bridge before building began on the Tyne Bridge.
The confusion arises because the Sydney Harbour Bridge took longer to complete due to its larger size.
The Sydney Harbour Bridge finally opened in 1932, three years after the Tyne Bridge.”
Minecraft Sydney Harbour Bridge
The following video shows a “Minecraft” reproduction of the Sydeney Harbour Bridge.
There isn’t all the detailed triangulation, but the basic parabolic structure is a very good look a like.
Also notice in the build that there are less horizontal blocks at the beginning of each arch, and then progressively longer rows of horizontal blocks towards the top. This demonstrates the changing gradient properties of the parabolic shape quite well.
Related Items
Tall Buildings and Huge Water Dam
Mathematics of the Melbourne Cup
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PDF containing the Bridge Measurements Photos, and accompanying instructions for a mathematics class to calculate the Bridge’s Quadratic Equations, 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Sydney Harbour Bridge Parabolas” PDF.
Email Subscription to Passy’s World is Free. To find out exactly how free subscription works, click the following link:
Like Us on Facebook
Our Facebook page has many additional items which are not posted to this website.
These include items of mathematical interest, funny math pictures and cartoons, as well as occassional glimpses into the personal life of “Passy”.
Check it out at the following link:
https://www.facebook.com/PassysWorldOfMathematics
While you are there, LIKE the page so you can receive our FB updates to your Facebook News Feed.
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Enjoy,
Passy





Pingback: Big Measurements | Passy's World of Mathematics
Pingback: Mathematics of the Melbourne Cup | Passy's World of Mathematics
Pingback: Expanding Two Brackets Binomials | Passy's World of Mathematics