
Image Source: http://www.strangezoo.com
Here at Passy’s World we use the “Crab Claws” method to Expand expressions which consist of two brackets.
It takes all the pain out of expanding these items, although messing with a real crab’s claws could cause some severe discomfort.
Why We Learn Expanding Brackets

Image Copyright 2013 by Passy’s World of Mathematics
Expanding Brackets does not achieve much on its own, but is a basic skill we need for doing a lot of other mathematical work.
Here at Passy’s World we developed an Algebra Equation for the Sydney Harbour Bridge in Australia.
We did this from scaling a photo we took of the Bridge, starting off by knowing that the bridge is 503 meters long.
This scaling involved using Ratio and Proportion. We took the number of pixels on the Photo which Adobe Photoshop gave us for the length of the Bridge, and divided this by 503m.
This gave us a Scale Factor value of 0.81 Pixels per Meter.
We could then apply this multiplying scale factor to all of our other Pixel lengths, and thereby convert them into meters.
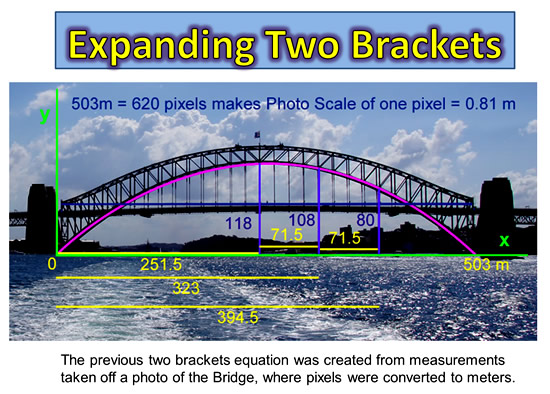
Image Copyright 2013 by Passy’s World of Mathematics
To produce the graph of the Bridge, we needed to expand our brackets equation into a simplified equation that could then be entered into an Online Graphing Application.
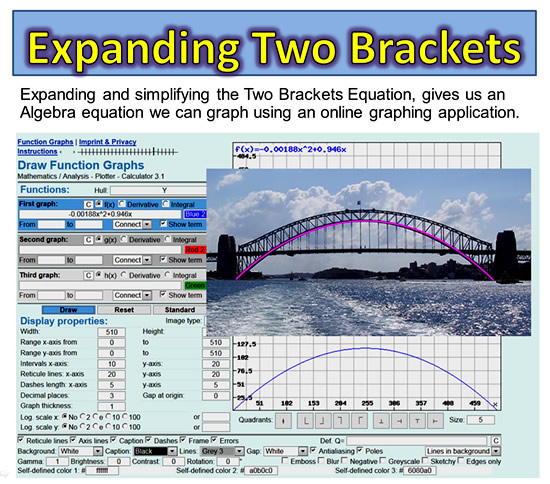
Image Copyright 2013 by Passy’s World of Mathematics
We could then prove that our equation for the Bridge was correct, because its graph exactly matched the real life shape of the Bridge.
Accurate Graphing is just one reason why we need to know how to expand brackets. We also need to know how to expand brackets to make it easier to solve Algebra Equations.
If you would like to know more about the mathematics of the amazing Sydney Harbor Bridge, then check out our previous lesson all about this at the following link:
http://passyworldofmathematics.com/sydney-harbour-bridge-mathematics/
Expanding Two Brackets Containing Numbers
The easiest way to do these is using BODMAS of Pemdas, but there is another method known as “Binomial Expansion” which will also get us the correct answer.

Image Copyright 2013 by Passy’s World of Mathematics
Using the Order of Operations gives us the answer of 45.

Image Copyright 2013 by Passy’s World of Mathematics
Now let’s look at how we can get the same answer of 45, but by using the “Binomial Expansion” method.
This method involves multiplying and adding together the four numbers in our brackets in a specific set order.

Image Copyright 2013 by Passy’s World of Mathematics
We would not want to use the above method in real life, because it is much more work than using BODMAS or Pemdas.
HOWEVER: This longer “Binomial Expansion” method gives us a way of expanding brackets which contain Algebra letter variables.
We cannot use BODMAS or Pemdas on Algebra brackets, and they need to be done using the Binomial Expansion Method.
The “Crab Claws” Method

Image Copyright 2013 by Passy’s World of Mathematics
An easy way to remember the Binomial Expansion Pattern, is to use the “Crab Claw” method shown above.
We suggest you always draw out the two crab claws onto the brackets first, and then do all of the multiplying and adding of items.

Image Copyright 2013 by Passy’s World of Mathematics
Binomial Expansions Examples
Our first example involves expanding the expression: (h + 3) (y + 5)

Image Copyright 2013 by Passy’s World of Mathematics
Notice that we started off with four different items in the brackets: the h, 3, y, and 5.
Because we have done four multiplications during the Crab Claws expansion, we end up with a four part answer.
This final answer is simply left as a four term Algebra Expression, and it cannot be simplified any further.
Here are some further examples of Binomial Expansions using the Crab Claws method.

Image Copyright 2013 by Passy’s World of Mathematics
This example was a little trickier than our first one, because it has a minus sign subtraction in one of the brackets.
The four items in (k + 2)(v – 1) are k, 2, v, and -1.
This means that we get some Integer Multiplications to do in the expanding, and so we need to remember and apply our Integer Multiplication Rules:
These Integer Multiplication Rules can be summarised as follows:
The following example for Expanding (m-2)(n-6) contains the items: m, -2, n, and -6, which will mean we have some Integer Multiplications to do.

Image Copyright 2013 by Passy’s World of Mathematics
In this next example, we have some slightly larger terms to deal with, but we still use the same “Crab Claws” method to get our final answer.

Image Copyright 2013 by Passy’s World of Mathematics
Expanding and Answer Sizes
In Examples 1 to 4 that we have done so far, we had four different items in our brackets at the start, and this resulted in four separate terms in our final answer.
HOWEVER: Not all Binomial Expansions have a Four Part Answer.
For some Binomials we are able to add or subtract some “Like Terms”, and reduce down to a “Three Part” final answer, or even in some cases a “Two Part” final answer.
If you are not sure about how to do “Like Terms” simplifying, then review “Combining Like Terms” using our previous lesson at the link below:
http://passyworldofmathematics.com/combining-like-terms/
For Binomial Expansions, we can get four, three, or even two part answers; depending on how many “Like Terms” we had back in our starting brackets.

Image Copyright 2013 by Passy’s World of Mathematics
The following examples show how we get “Three Part” and “Two Part” final answers.
Like Terms Binomial Expansions
For the brackets: (m + 4) (m + 1) we only have three different items: the m, 4, and 1.
This results in a “Three Part” final answer as shown below.

Image Copyright 2013 by Passy’s World of Mathematics
The Binomial: (b – 3) (b – 2) is another example where we get a three part answer.
The original brackets only contain three different starting items: the b, -3 and -2.

Image Copyright 2013 by Passy’s World of Mathematics
Here is another example which produces a “Three Part” final answers.

Image Copyright 2013 by Passy’s World of Mathematics
Two Part Final Answer Binomial Expansions
Whenever we have (Item One + Item Two) (Item One – Item Two) we get a final answer which contains only two terms.
There is even a Shortcut Rule for this called the “Difference of Perfect Squares” or “D.O.P.S. Rule.
Here is a typical example of this type of expansion.

Image Copyright 2013 by Passy’s World of Mathematics
Larger Items Binomial Expressions
Sometimes our starting brackets contain not just single letter items like “y” or “a” or “m” etc, but instead we have larger items such as “3y” or “2a” or “-5m”.
This is not really an issue at all, we simply do our “Crab Claws” method expansion as usual, and simplify any like terms that are produced along the way.
The following example shows how to do one of these Larger Items Expansion

Image Copyright 2013 by Passy’s World of Mathematics
Expanding Squared Brackets
When our starting question has one set of brackets squared, we need to first write it out as two brackets.
Five Squared means 5 x 5 and so (y + 5)^2 simply means (y + 5)(y + 5) .
Once we make this starting adjustment, we can then do our “Binomial Expansion” as normal using the “Crab Claws” method.
The following is a typical example of this type.

Image Copyright 2013 by Passy’s World of Mathematics
Note that there is a shortcut rule for these type of expansions which is called the “Perfect Squares Rule”.
However, here at Passy’s World we find it much easier to just use the “Crab Claws” method, and so we have not covered this shortcut rule in this lesson.
“FOIL” Rule for Binomial Expansions
You may hear of the “Crab Claws” pattern being called the “F.O.I.L.” Rule.
FOIL stands for “First” “Outside” “Inside” “Last” and is just another way of describing the four step expansion pattern that we use.
If you would like to see the “FOIL” version of the “Crab Claws” method in action, then check out the following video.
Related Items
Distributive Property Expansion Rule
Integers Multiplication Rules
Combining Like Terms
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Expanding Two Brackets” Powerpoint.
Like Us on Facebook
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy







Pingback: Factorising With Common Factors | Passy's World of Mathematics