
Image Source: http://www.photl.com
Total Surface Area (“TSA”) is important for Painters, so that they know how much paint will be required for a job.
Engineers, Designers, Scientists, Builders, Concreters, Carpet Layers, and other occupations also use Total Surface Areas as part of their work.
In this lesson we show how to calculate the Total Surface Area of Rectangular and Triangular Prisms, including Cylinders, as well as the TSA of Pyramids.
TSA of Rectangular Prisms
One method of calculating the TSA (Total Surface Area) is to “unfold” a 3D shape, into its flat “2D” net which the shape is made from.
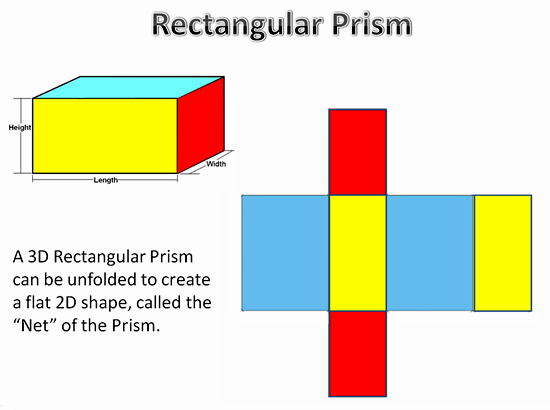
Image Copyright 2013 by Passy’s World of Mathematics
From the above Net, we can see that a Rectangular Prism is made of 3 pairs of Rectangles, which creates a Net containing a total of six rectangles.
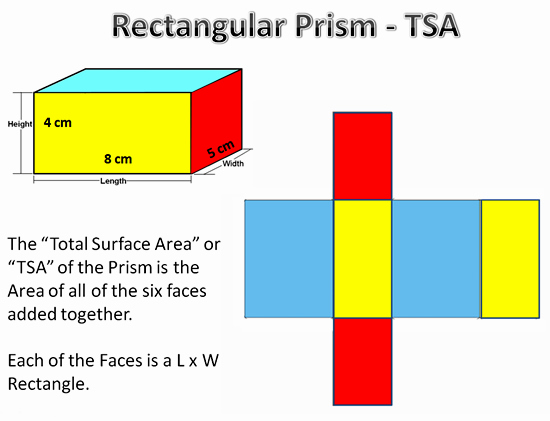
Image Copyright 2013 by Passy’s World of Mathematics
To determine the TSA, we need to find the area of all six rectangles, and then add up these areas to find the total area.

Image Copyright 2013 by Passy’s World of Mathematics
The following video shows how to calculate the Volume of a Rectangular Prism by unfolding it into its Net.
TSA Formula For Rectangular Prisms
If we assign Algebra letter values for Length, Width, and Height on a Rectangular Prism, we can work out the following general Formula for the TSA of any Rectangular Prism.
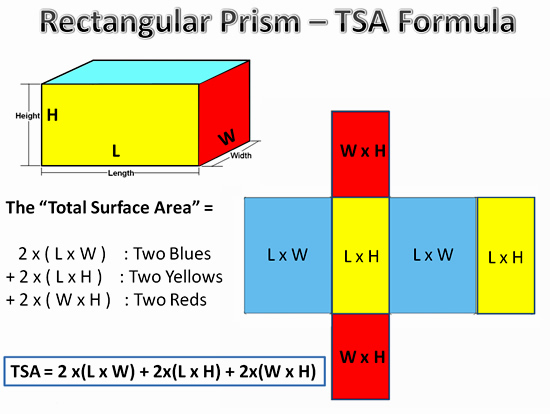
Image Copyright 2013 by Passy’s World of Mathematics
The following Video shows how to derive the above TSA formula for a Rectangular Prism.
TSA of Rectangular Prisms Using the TSA Formula
The following Video shows how to calculate the TSA of a rectangular Prism without using Nets.
If we have the Length, Width, and Height values for a Rectangular Prism, we can calculate its TSA by using the TSA Formula.
This saves us having to draw out the flat 2D Net of the shape.
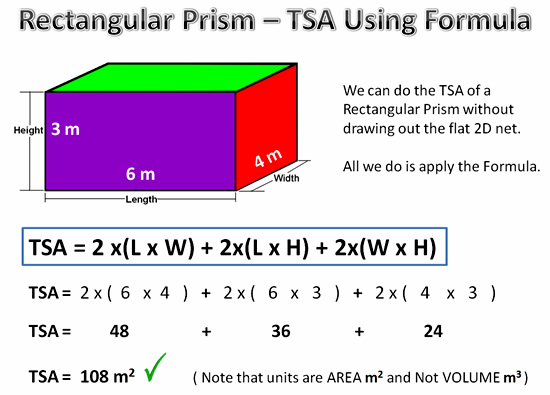
Image Copyright 2013 by Passy’s World of Mathematics
The following Video shows how to calculate the TSA of a Rectangular Prism using both Nets and the Formula.
This next video goes through a Practical problem about painting a wooden chest.
TSA of Triangular Prisms

Image Source: http://3.bp.blogspot.com
The Toblerone chocolate bar packaging is a classic example of a Triangular Prism.
One method of calculating the TSA (Total Surface Area) is to “unfold” a 3D shape, into its flat “2D” net which the shape is made from.
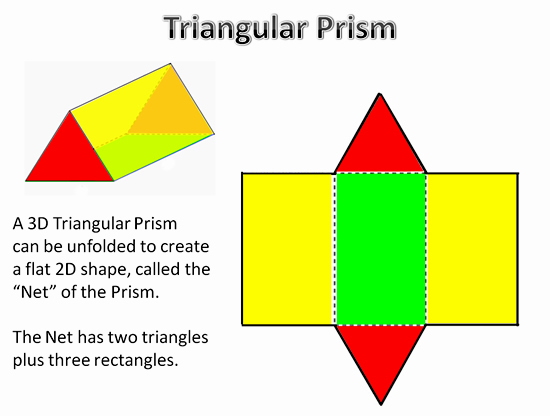
Image Copyright 2013 by Passy’s World of Mathematics
If we have measurements for our Triangular Prism, then we can calculate the TSA using the shapes on the 2D Net.

Image Copyright 2013 by Passy’s World of Mathematics
TSA Formula For Triangular Prisms
If we assign Algebra letter values for Length, Width, Height, and Sloping Side Leght on a Triangular Prism, we can work out the following Formula for the TSA of a symmetrically shaped Triangular Prism.
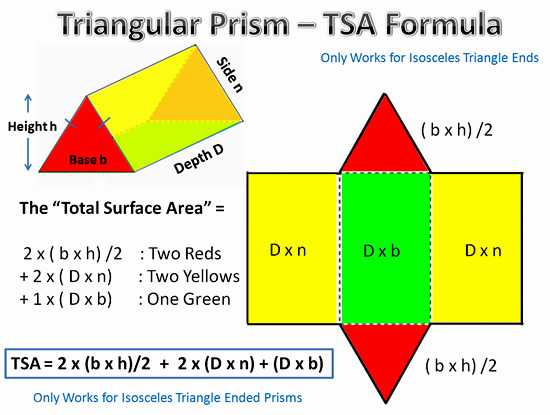
Image Copyright 2013 by Passy’s World of Mathematics
The above formula only works for Triangular Prisms which have Isosceles or Equilateral Triangular ends.
The problem with Triangular Prisms, is that we can have triangular ends which are not symmetrical, as shown in the example below.
These irregular triangles do not follow our formula.
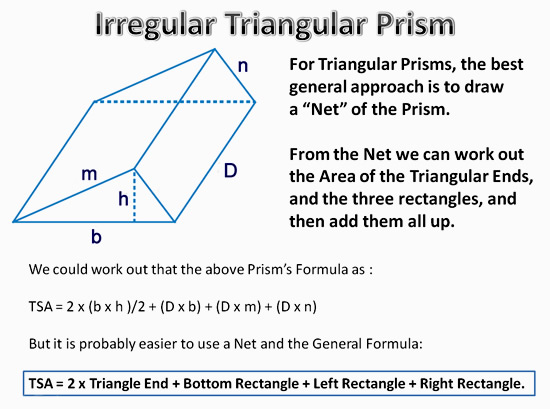
Image Copyright 2013 by Passy’s World of Mathematics
Therefore we usually create Nets for all Triangular Prisms and then use the General Approach:
TSA = 2 x Triangle End + Bottom Rectangle + Left Rectangle + Right Rectangle.
Pythagoras Theorem and Triangular Prisms
If we are given a Triangular Prism, with only the side measurements, and we do not have its Height; then we can use Pythagoras Theorem to find the Height.
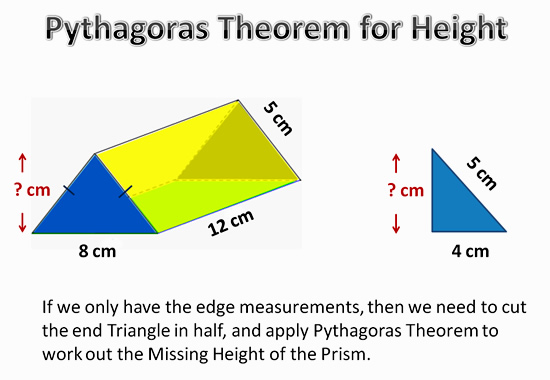
Image Copyright 2013 by Passy’s World of Mathematics
The following Video (which is in two parts), shows how to use Pythagoras Theorem on Triangular Prisms.
Here is Part 2 of the Video:
TSA of Cylinders
One method of calculating the TSA (Total Surface Area) is to “unfold” a 3D shape, into its flat “2D” net which the shape is made from.
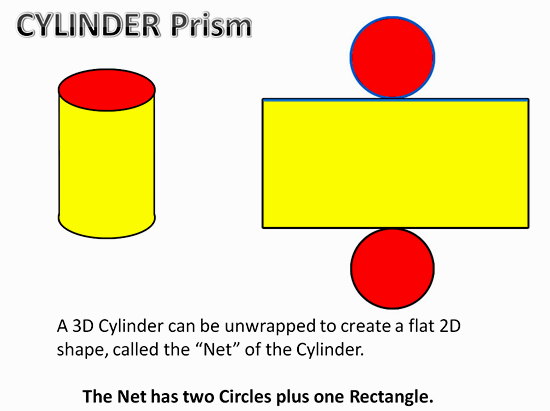
Image Copyright 2013 by Passy’s World of Mathematics
The following video shows how a 3D Cylinder is unwrapped into its 2D Net.
Consider the following Cylindrical Water Tank with a Height of 10m and Radius of 2m.
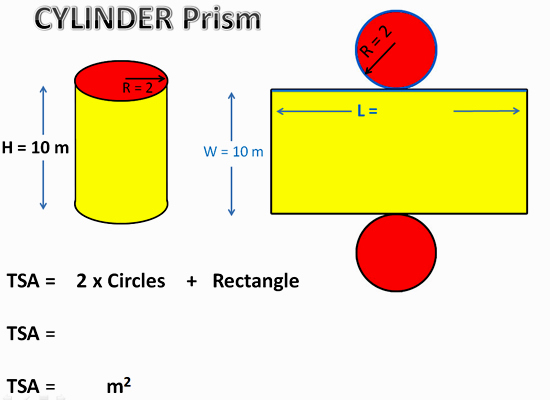
Image Copyright 2013 by Passy’s World of Mathematics
Working out the Area of the Rectangle involves using the Circumference of the circle which the Rectangle is wrapped around.
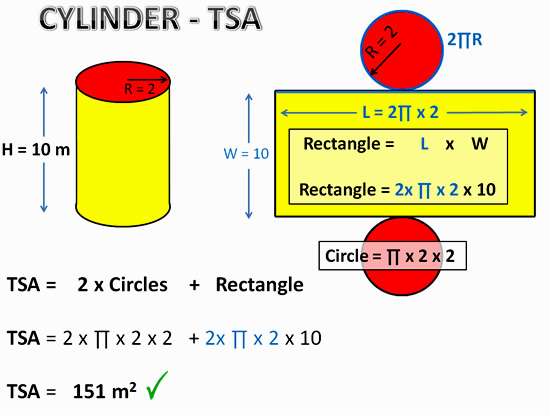
Image Copyright 2013 by Passy’s World of Mathematics
TSA Formula For Cylinders
If we assign Algebra letter values for the Radius and Height on a Cylinder, we can work out the following general Formula for the TSA of any Cylinder.

Image Copyright 2013 by Passy’s World of Mathematics
Here at Passy World we find it much easier to use the TSA Formula for solving problems involving Cylinders.
We prefer using the formula to drawing out a Cylinder’s 2D Net and working out the separate shapes from the Net.
TSA of Cylinders Using the TSA Formula
If we have the Radius and Height values for a Cylinder, we can calculate its TSA by using the TSA Formula.
This saves us having to draw out the flat 2D Net of the shape.

Image Copyright 2013 by Passy’s World of Mathematics
TSA of an Open Top Cylinder
The following video shows how to calculate the TSA of a Cylinder which does not have a top on it.
TSA of a Half Cylinder
The following video shows how to calculate the TSA of a Half Cylinder.
TSA of Square Based Pyramid
Pyramids are not Prisms because they do not have a uniform cross section.
However we can still draw nets for them and calculate their TSA.
A 3D Square Egyptian type Pyramid unwraps to a 2D Net that contains one central square, surrounded by four equal triangles.

Image Copyright 2013 by Passy’s World of Mathematics
The following example shows how to calculate the TSA of a Square Pyramid.
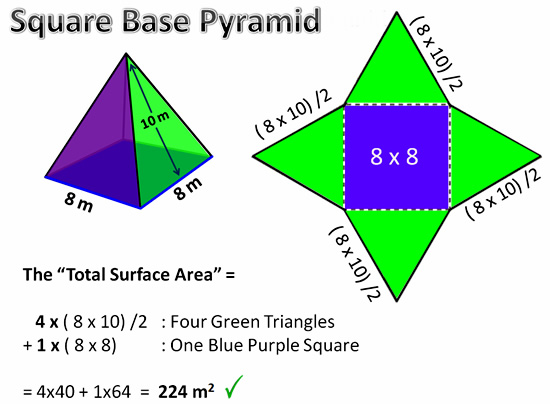
Image Copyright 2013 by Passy’s World of Mathematics
TSA Lesson Plan for Teachers
Here at Passy’s World we have found the best way to learn TSA is to first start with the Nets of the 3D Solid Prisms.
The following PDF document contains the Nets for Rectangular Prism, Triangular Prism, and Cylinder.
http://passyworldofmathematics.com/pwmPDFs/NetsofSolids.pdf
Students are given a printed copy of these nets, and for each shape, cut the net out, fold it to see how it makes the 3D shape, but do NOT glue it together.
Instead stick it down flat into their math workbook, with the 3D shape image with it on the same page.
For each shape we then work through a Prism with number values on it, and write the working out of areas directly onto the flat Net.
They then add up all these areas on the Net to get the Total Surface Area.
Later we move on from using nets of Rectangular Prisms and Cylinders, to simply using the mathematical formulas for the TSA of these shapes.
Related Items
Free Online Calculators and Converters
Measurement Formulas
Converting Metric Units
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Total Surface Area” Powerpoint.
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy




