Exponents in the Real World

Exponents, Index Numbers, Powers, and Indices are used in lots of parts of our modern technological world.

Exponents are used in Computer Game Physics, pH and Richter Measuring Scales, Science, Engineering, Economics, Accounting, Finance, and many other disciplines.

Exponential Growth is a critically important aspect of Finance, Demographics, Biology, Economics, Resources, Electronics and many other areas.

Exponential Decay is associated with Light, Sound, Sporting Fixtures, Dangerous Chemicals, and Radioactive Waste.

People who use Exponents are Economists, Bankers, Financial Advisors, Insurance Risk Assessors, Biologists, Engineers, Computer Programmers, Chemists, Physicists, Geographers, Sound Engineers, Statisticians, Mathematicians, Geologists and many other professions.

In this lesson we show several Real Life uses of Exponents, as well as their impact on our understanding of the modern world around us.

Exponents are fundamental, especially in Base 2 and Base 16, as well as in Physics and Electronics formulas involved in Computing.

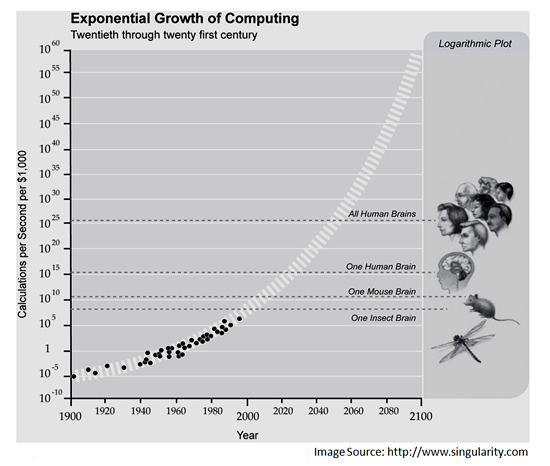
There has been an Exponential increase in the speed and power of computers over recent years, and by around 2030 computing power is predicted to match that of the human brain.

Exponents are critcally important in modern Internet based Sales and Marketing,

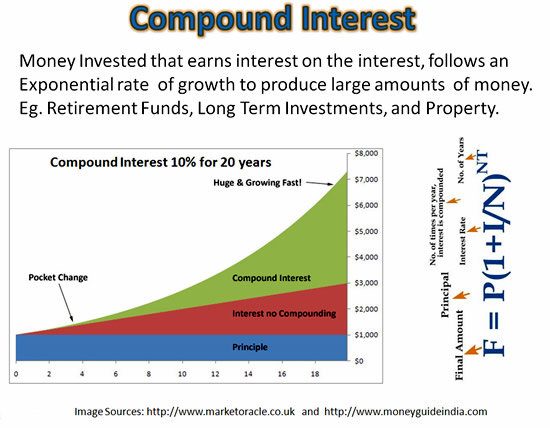
Exponents are important in Investing and Finance.

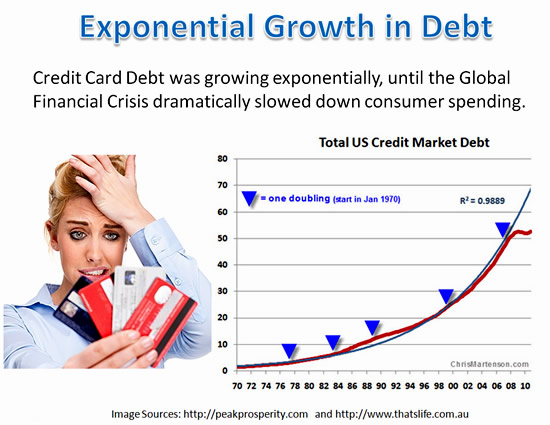
Compound Interest also works against people with a Credit Card debt they do not pay off, because the debt grows faster and faster each billing period and can quickly become out of control.
 
 

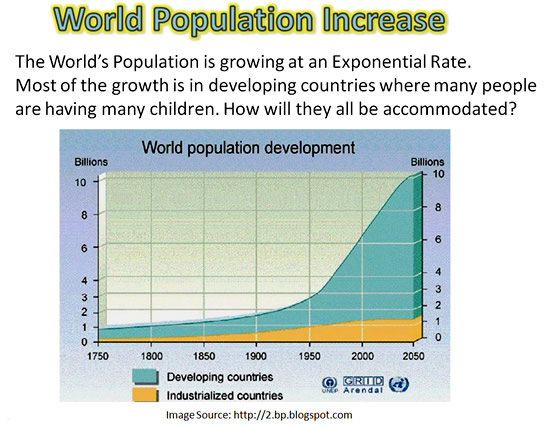
Exponents are the basis of “Demographics” (Population Growth)

The World’s Population is increasing at an extraordinary rate, especially in the devloping regions of Africa, India, and China.

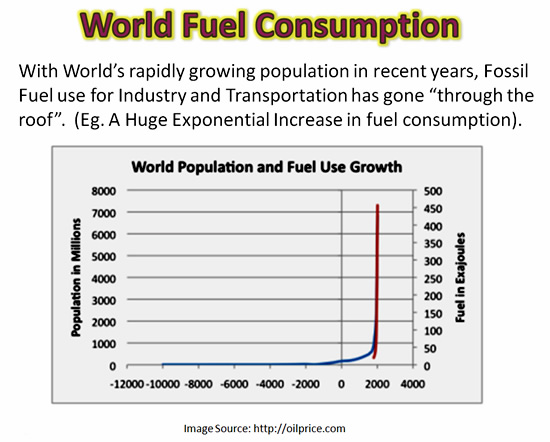
With massive Population Growth comes massive use of Fossil Fuels for Industry, Heating, Electricity, and Transportation.

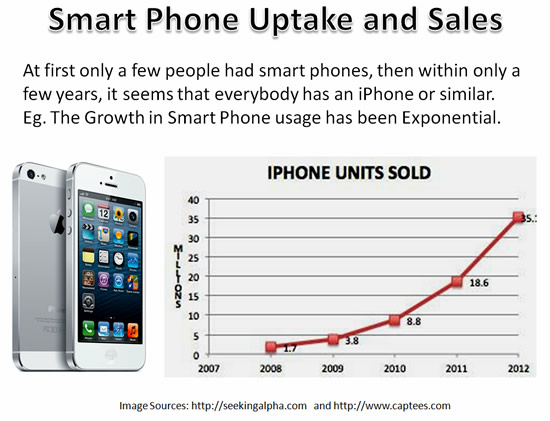
Over the last few years there has been massive exponential increases in mobile phone usage and market penetration.

Consumer Credit Debt has increased over recent years to record high levels.

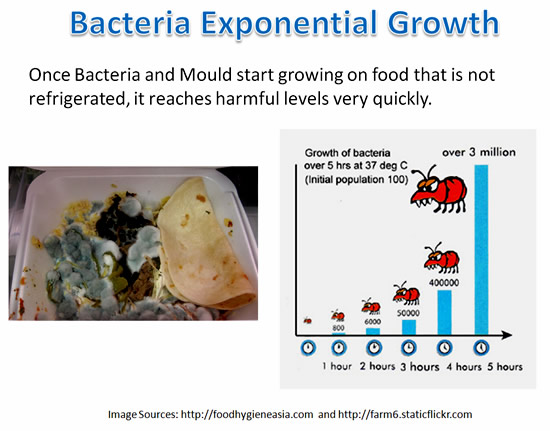
Exponents are also part of Food Technology and Microbiology.

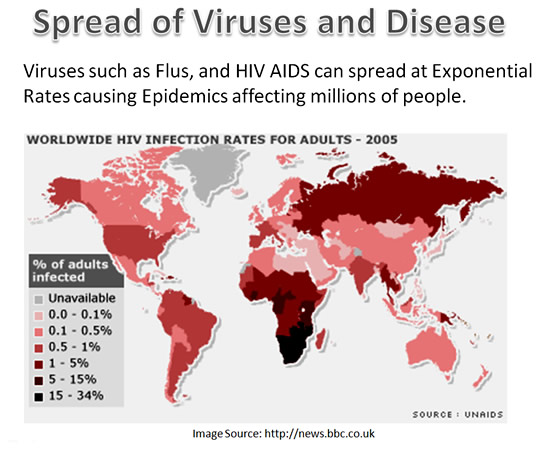
Virus Illness, (as well as many email and computer viruses), can spread at ever increasing rates causing major widespread infected areas.

This happens the same way that Viral Marketing branches out in ever increasingly wide branches of more and more people passing something onto more and more other people.

In explosions we get an uncontrolled massively increasing output of energy and force within a very short time period.

Picture this as a very steep exponential graph, compared to a burning match giving out energy in a fairly flat straight line graph.

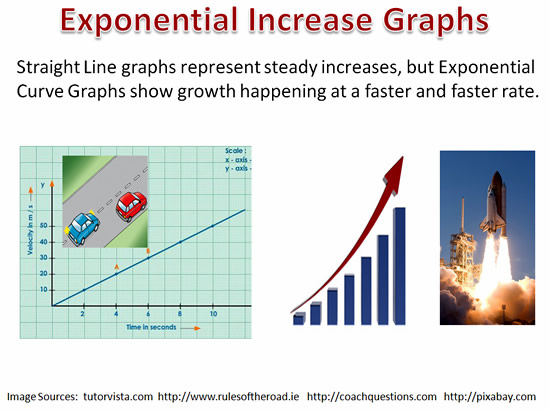
Exponential Growth

The situations we have been considering so far involve “Exponential Growth”.

The equations for graphs of these situations contain exponents, and this results in the graph starting off slow, but then increasing very rapidly.

Eg. Think of Square Numbers and how they quickly get bigger and bigger:

1 4 9 16 25 36 49 64 81 100 121 132 etc

It only takes us nine square numbers to reach 100.

Exponential Growth situations when graphed look like the diagram below.

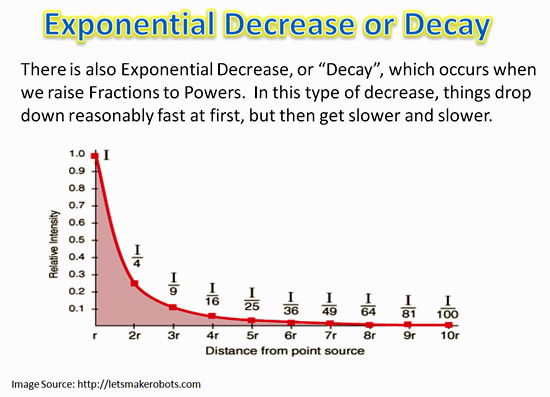
The opposite of “Exponential Growth”, is when we apply exponents to fractions which results in “Exponential Decay”.

Exponential Decay

Using negative power values results in fractions, and when these fractions have exponents applied to them we get “Decay”.

In a “Decay” process the amount involved drops off fairly quickly at the start, but then the drop off becomes slower and slower.

A typical Exponential Decay graph looks like this:

Making an Exponential Decay Graph

Image Source: http://teachers.egfi-k12.org

A fun way to make an Exponential decay graph is to take a pack of M&M’s or Skittles and keep pouring them out of a cup, but each time removing any candies which land with the letter side showing.

This should produce the required graph.

There is a great set of instructions on how to do this at the following link:

Click Here for M&Ms Exponential Graph Instructions

Exponential Decay – Real Life Examples

Some examples of Exponential Decay in the real world are the following.

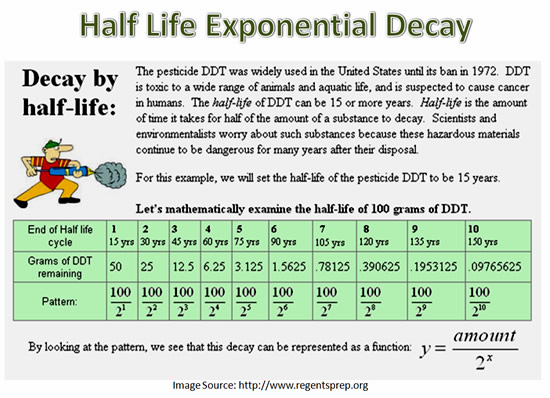
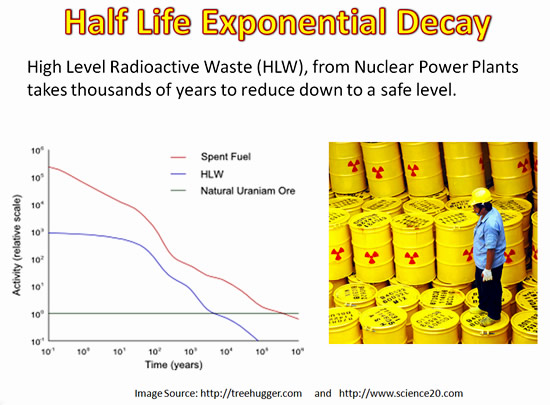
Exponential Decay and Half Life

Many harmful materials, especially radioactive waste, take a very long time to break down to safe levels in the environment.

This is because these materials undergo exponential decay, and even a small amount of the material still remaining can be harmful.

Exponential Scales

The Richter Scale is used to measure how powerful earthquakes are.

The actual energy from each quake is a power of 10, but on the scale we simply take the index value of 1, 2, 3, 4, etc rather than the full exponent quantity.

This means that a Richter Scale 6 earthquake is actually 10 times stronger than a Richter Scale 5 quake. (Eg. 1000000 vs 100000).

Likewise, a Richter Scale 7 earthquake is actually 100 times stronger than a Richter Scale 5 quake. (Eg. 10000000 vs 100000).

The pH Scale for measuring the Acidity of materials is also created by taking the Power Values from measured powers of 10 acid concentration values.

Exponents and Scientific Notation

Very large numbers, like the distance between planets, or the population of countries, are expressed using powers of 10 in a format called “Scientific Notation”.

Scientific Notation is also used for expressing very small decimal values like the size of flu virus molecules, or the distance between atoms in a crystal structure.

Online Presentation on Exponents in the Real World

An online presentation of this lesson is available on SlideShare at the following Link:

Click here for our SlideShare Presentation
 
 

Music Video About Exponents

The following music video all about Exponents, is possibly the most successful Math video ever uploaded to YouTube.

It has currently had over 850,000 views on YouTube and is quite an amazing Production!

Well worthy of viewing by anyone learning Indices and Exponents.

Related Items

Basic Indices and Exponents
Multiplying Exponents
Dividing Algebra Expressions
Dividing Exponents Using Subtraction Rule
Expanding Exponents Using Power of Power Rule
Expanding Exponent Products Rule
Expanding Exponent Quotients Rule
Zero and Negative Exponents
Scientific Notation

Subscribe

If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.

Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.

To find out exactly how free subscription works, click the following link:

How Free Subscription Works

If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.

Like Us on Facebook

Help Passy’s World Grow

Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.

Help us to maintain this free service and keep it growing.

Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!

PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.

Enjoy,
Passy