
Image Source: http://img.ehowcdn.com
Often our Calculator gives us very long answers which need to be rounded off to have a smaller number of “Significant Figures”.
For example, if we measure the Height of all the students in our class, and use a calculator to get an average, we might get an answer like 172.3421 cm.
If we record this long answer as our average, then it imples we measured the students’ heights to an accuracy of 4 decimal places.
There is no way we are allowed to claim this level of accuracy, (unless we used $20 000 worth of very high tech laser measuring equipment!).
We probably measured the heights with a ruler or a tape measure, and they are only accurate to the nearest whole number.
Our final answer for the Average Height neeeds to be written as 172cm, not 172.3421 .
Other real life situations also need us to think about how accurately a value has been measured.
The actual number of the people attending the above event might have been 14 687 or perhaps 15 215.
However we only need to know the figure to the nearest thousand, and so it is expressed as 15 000 or 15 thousand.
The 15 is the important part of the value, the three zeroes on the end just tell us that it is in units of thousands.
We say that 15 000 has two significant figures.
Significant Figures are used a lot in Science, Economics, Statistics, Finance, and many other areas of life where we are measuring things to a certain level of accuracy.
Significant Figures and Exact Values
The Significant Rules figures we are covering in this lesson must never be applied to “Exact Values”.
In the previous example of the estimated crowd size, we were given the five figure value of 15 000, and worked out that it had only two Significant figures.
This is the correct answer for 15 000 as a measured value in this particular situation.
However, the value of 15 000 does not always have two Significant Figures.
If we have an EXACT VALUE, like you are borrowing $15 000 from the bank for a Car, then this needs to be exactly $15 000, (not $14 821 or $15 100 or any other value).
A $15 000 transaction with the Bank is always a 5 Significant Figures value, because it involves EXACTLY $15 000 (and is not an estimated or rounded off value).
A Freeway Speed Limit of 100 km/hr is also an Exact Value, and has three significant figures.
An Exam Pass cutoff level of 50% is an exact value, and has two significant figures.
Significant Figures Rules
There is a set of fairly complicated rules for working out how many “Significant Figures” are in a given number or decimal value.

Image Copyright 2013 by Passy’s World of Mathematics
Here at Passy World we find it easier to use Scientific Notation to work out the number of Significant Figures, rather than use all of these rules.
However if you would like to use these rules, then check out the following video which shows you how.
The video at the link below also covers these five Significant Figures rules extremely well:
Click Here for Signicant Figures Video
Using Scientific Notation for Significant Figures
If we put our number or decimal value into Scientific Notation, it is very easy to work out the number of Significant Figures.

Image Copyright 2013 by Passy’s World of Mathematics
Once our number or decimal is in Scientific Notation, all we do is count how many digits there are!
If you do not know how to do Scientific Notation, then check out our lesson on this at the link below:
Click here for our lesson on Scientific Notation
Important Helpful Hints
Whenever doing Scientific Notation and Significant Figures, always keep the following in mind.
Normal Numbers bigger than 1, or large numbers,always have a POSITIVE Power of 10.
Values smaller than 1, usually decimal values,always have a NEGATIVE Power of 10.
The first part of Scientific Notation is always a number value that is between 1 and 10. (eg. 1, 2.345, 3.65, 6.310, 7.0, 8.5, 9.9999 etc)
The second part of Scientific Notation is a Power of 10 which tells us how many places the decimal point is moving.
The resulting number of digits in our 1 to 10 number is the number of Significant Figures.

Image Copyright 2013 by Passy’s World of Mathematics
Determining Significant Figures Examples
The following examples show how we can put a number or decimal value into Scientific Notation, and then very easily determine its “Number of Significant Figures”.

Image Copyright 2013 by Passy’s World of Mathematics

Image Copyright 2013 by Passy’s World of Mathematics

Image Copyright 2013 by Passy’s World of Mathematics
We can also determine the number of Significant Figures in Decimal Values.

Image Copyright 2013 by Passy’s World of Mathematics
The following example shows a very important exception rule for removing zeroes from Decimal values that we are converting into Scientific Notation.
ANY ZERO THAT CAME AFTER THE DECIMAL POINT IN THE ORIGINAL STARTING DECIMAL NUMBER MUST NOT BE REMOVED.
It must not be removed because it is a Significant digit.
The reason why is a little complicated, but works like this.
If somebody wrote down a measurement as 0.0050, this means they measured it to four decimal places to the nearest ten thousandth, and it is 50/10000. The “50” in 50 thousandths has two Significant Figures.
If they had only measured it to three decimal places to the nearest thousandth, then the value would have been recorded as 0.005 and it is 5/1000. The “5” in 5 thousandths has one Significant Figure.
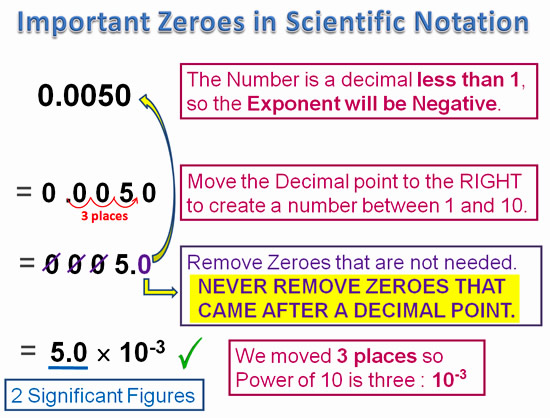
Image Copyright 2013 by Passy’s World of Mathematics
Here is another example that has an ending decimal zero value which is Significant and must not be removed.

Image Copyright 2013 by Passy’s World of Mathematics
Significant Figures and Rounding Off
If we convert our number or decimal value into Scientific Notation, then we can round if off using normal rounding off rules.
Rounding Rules involve the following:
Work out where we are rounding off to, and then look at the next digit after this:
If this next digit is 0 to 4 (0, 1, 2, 3, 4 ) then “Do no More” and discard all the extra not needed digits.
If this next digit is 5 to 9 (5, 6, 7, 8, 9 ) then “Up this Time” and add on one, and then discard all the extra not needed digits.
Just remember: “0 to 4 Do No More”, or “4 and below, Let it Go”.
To review Rounding Off if you are not too sure about how it works, then check out our lesson on Rounding Off at the following link:
Click here for Rounding Off Lesson
Rounding Off Examples
The steps to Rounding off are:
Convert our given Value into Scientific Notation
Round off to the required Significant Figures
Convert the rounded off Scientific Notation back to a normal Number or Decimal values.
In the following two examples we are Rounding Off to TWO Significant Figures.
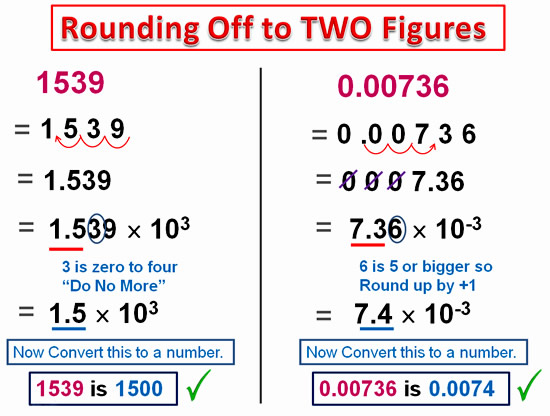
Image Copyright 2013 by Passy’s World of Mathematics
In the following two examples we are Rounding Off to THREE Significant Figures.

Image Copyright 2013 by Passy’s World of Mathematics
Related Items
Indices and Exponents in the Real World
Basic Indices and Exponents
Multiplying Exponents
Dividing Algebra Expressions
Dividing Exponents Using Subtraction Rule
Power of Power Exponents Rule
Expanding Exponent Products
Expanding Exponent Quotients
Zero and Negative Exponents
Scientific Notation
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Significant Figures” Powerpoint.
Like Us on Facebook
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy





