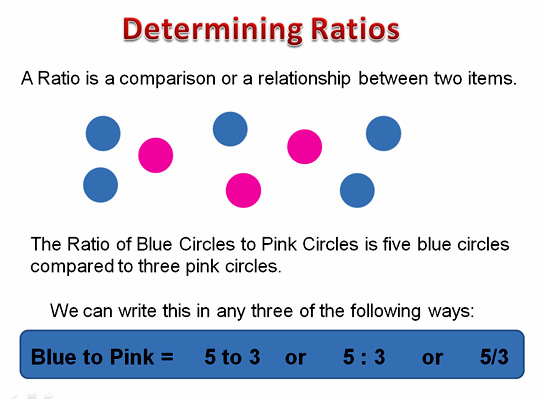
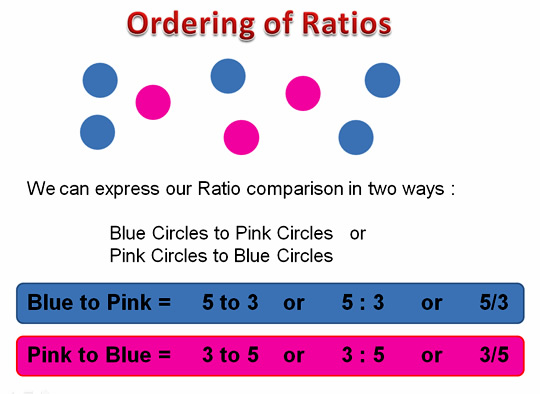
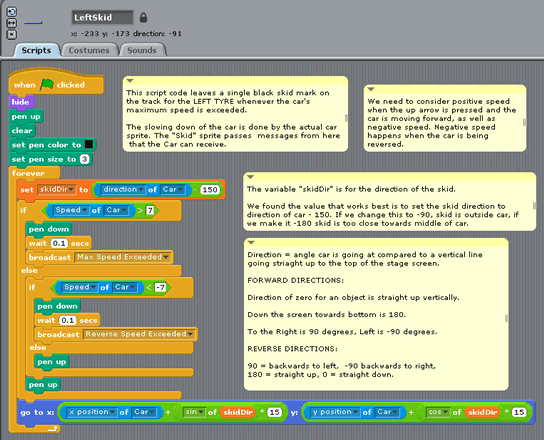
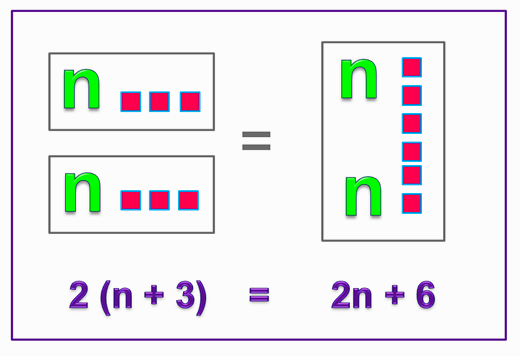
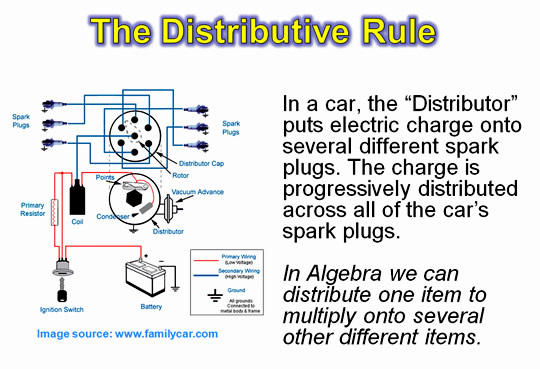
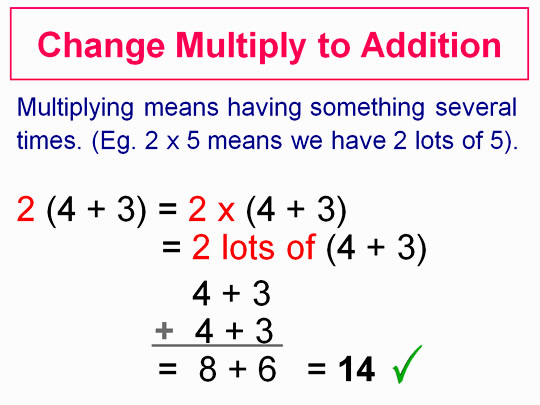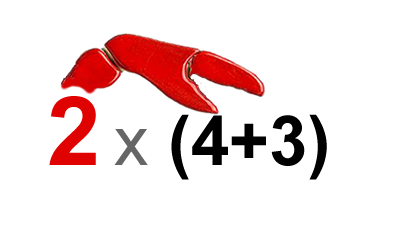Ratios and Proportions are used for cooking as well as making drinks.
A strawberry milkshake can be made by mixing together in a blender 2 parts strawberry ice cream to 7 parts of milk.
This can be written in Ratio form as 2 : 7 which in fraction from equals 2/7 .
Both forms mean the exact same thing, which is 2 parts ice cream to every 7 parts of milk.
However when we use two scoops of ice cream and seven scoops of milk, we find that we don’t get enough milkshake to completely fill our two big glasses.
So we decide next time to make a milkshake using three scoops of ice cream.
How do we make a milkshake using three scoops of ice cream ?
How much milk do we need to use to get the correct consistency ?
We can calculate the exact amount of milk required by using Ratios.
We write out two ratios and make them equal to each other.
This is called making a “Proportion”.
A “Proportion” is simply two ratios which are equal to each other.
The two ratios can be written out in shorthand from such as 2 : 7 = 3 : m
or as a pair of fractions such as 2/7 = 3/m
where “m” = the number of scoops of milk, (which we do not know the number value of yet).
Here is how we mathematically solve our Strawberry Milkshake Problem, and find out how much milk we need for three scoops of ice cream.


Image Copyright 2012 by Passy’s World
Videos About Cross Multiplying
Cross Multiplying is probably a new method for many people, and the following video shows several examples of solving ratio proportions by Cross Multiplying.
This video writes the pairs of ratios as fractions.
Eg. x : 6 = 2: 3 is written as x/6 = 2/3
Remember any ratio can always be rewritten as a fraction :
a : b = a / b
Also remember that when we have two ratios (or fractions) that are equal to each other, then we call this situation a “Proportion”.
Here is another video about Proportions and Cross Multiplying.
Steps For Finding Ratio Amounts
Instead of writing fractions, here at Passy World we like to write the two ratios out one above each other, and then do our cross multiplying.
It is the exact same method as writing out fractions, so feel free to use fractions notation if you prefer working in fraction form.
In Ratio Amounts we use “Cross Multiplying” and follow the working out steps shown below.

Image Copyright 2012 by Passy’s World
Solving Proportions Examples
In the following examples, we apply the standard steps of re-writing vertically, then cross multiplying, and finishing off by dividing by the number in front of the letter variable.
This gives us a number answer for our variable letter.

Image Copyright 2012 by Passy’s World

Image Copyright 2012 by Passy’s World
Ratios Applications Videos
This first video shows how to do a ratios word question involving a real world car trip time calculation.
Ratios and Cross Multiplying are involved with solving this problem.
This next video also shows hot to solve some typical ratio word questions involving real world applications.
Ratios Application Examples
The following examples show how to solve some ratios application problems.

Image Copyright 2012 by Passy’s World
Note that 2-stroke fuel ratios are often specified as 25 : 1 but it is not possible to fit this volume into a 5 litre fuel can.
As a result, 25 : 1 mixes are often made up as 24 : 1 mixtures of Petrol (Gasoline) and Oil.
A 24 : 1 mix gives slightly more oil per litre than a 25 : 1 mixture, but this 4% extra oil in the mix is not going to affect the running of the 2-stroke engine, or cause any other significant problems.
Note that we worked out there is 4% extra oil in a 24 : 1 mix as follows:
Oil as 1 part compared to 25 parts Petrol, equals 1/25 = 0.04
Oil as 1 part compared to 24 parts Petrol, equals 1/24 = 0.0417
% Extra Oil = (0.0417 – 0.04) / 0.04 x 100 % = 4.2 % = 4 % rounded off.
This calculation is not technically correct, because “Percent” is supposed to be “Parts in 100”, worked out from how many parts out of the total parts we have, and then multiplying this by 100 %.
We have not covered Ratios and Parts yet, but a 1 : 25 mix means we have 1 part Oil and 25 parts Petrol, to make a total parts amount of 26.
So the Oil is actually 1 part out of 26 total parts = 1/26 = 0.0385.
The 1 : 24 mix actually has 25 parts total, (1 part Oil + 24 parts Petrol).
So the fraction of oil is actually 1 part out of 25 total parts = 1/25 = 0.04
% Extra Oil = (0.04 – 0.0385) / 0.0385 x 100 % = 3.9 % = 4 % rounded off.
Note that if we needed to make a 50 : 1 fuel mixture for a grass trimmer, or hedge clippers, then we could make this as a 49 : 1 mix, by putting 100 ml of oil in a 5 litre can, and then filling the rest of the can with 4900 ml of Petrol.

Image Copyright 2012 by Passy’s World
Related Items
Introduction to Ratios
Simplifying Ratios
Fibonacci Sequence in Music
If you enjoyed this post, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our blog, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson valued at $4.99, but 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Ratio Amounts and Proportions” PowerPoint.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Enjoy,
Passy