
Image Copyright 2012 by Passy’s World
If you have ridden a bike lately, then you will know that for going downhill very fast, we use a Rear Cog that does not have as many teeth compared to the Front Chain Ring.
This gives us a “Very High” Gear Ratio of 53 to 11.
Front / Rear gear measurement uses two numbers (e.g. 53/11) where the first is the number of teeth in the front chain ring and the second is the number of teeth in the rear sprocket.
Low Gear Ratios are used for going up hills, and a low gear Rear / Front Ratio might typically be 34 / 23, or 34 teeth on the rear cog, compared to 23 teeth on the front chain ring.
In Low Gear the chain ring will rotate more times than the cog, which gives us more power supplied to a single revolution of the rear wheel.
This makes it easier to get up a big hill.

Image Source: http://blog.jeffersonatwesttown.lincolnapts.com
Ratios are very important in Cooking.
If a recipe calls for 1 egg and 2 cups of flour, the relationship of eggs to cups of flour is 1 to 2.
Add the wrong ratios of ingredients to a baked cookies recipe, and the resulting salty rock hard cookies will not be a hit with anyone.

Image Source: http://www.goldjewelrytips.com
Ratios are also important in making gold for jewellery.
For example 14 carat Gold can be made by combining 6 parts Gold with two and a half parts Copper, and one and a half parts Silver.
The Ratio of Gold to Copper to Silver = 6 to 2.5 to 1.5
Definition of a Ratio
A Ratio is a comparison or a relationship between two items.
It is represented using a colon ‘:’, the word ‘to’ or using a fraction ‘/’.
For example, in the following diagram, the ratio of red cirles to blue circles is 5 to 3.
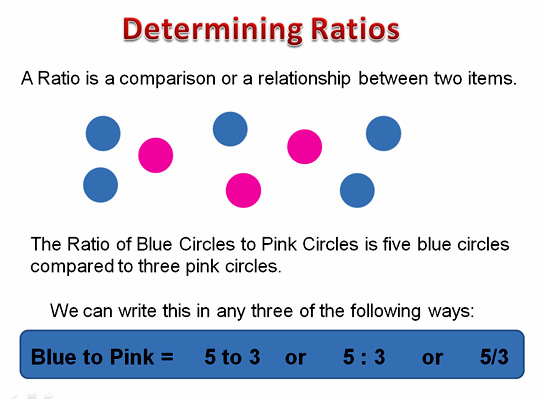
Image Copyright 2012 by Passy’s World
The order we write a ratio in is important. For our situation we can express the comparison Ratio in two different ways.
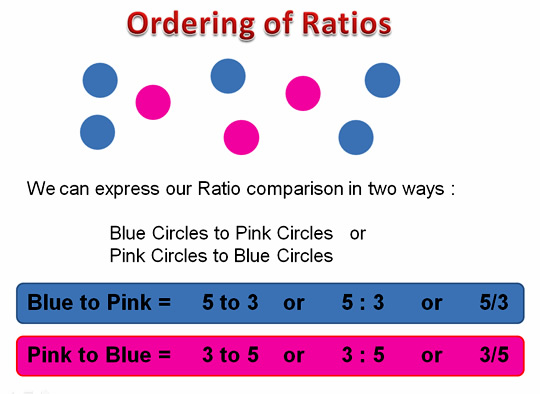
Image Copyright 2012 by Passy’s World
This means that we need to read math questions very carefully to see which order the Ratio needs to be written in.
If the question asked us to “write the Ratio of Blue Circles to Pink Circles”, then we would need to write 5 : 3 or 5 to 3.
The Ratio of Blue Circles to Pink Circles as 5 to 3 indicates that for every five Blue circles, we have three Pink Circles.
If we double our circles, we will have 10 Blue circles to 6 Pink circles.
There are still five Blue Circles for every three Pink circles. We simply now have two of these groupings.
We say that the ratio of 10 : 6 is “Equivalent”, (or means the same thing as), to 5 : 3 .

Image Copyright 2012 by Passy’s World
Introductory Video on Ratios
Determining Ratios Examples

Image Copyright 2012 by Passy’s World

Image Copyright 2012 by Passy’s World

Image Copyright 2012 by Passy’s World

Image Copyright 2012 by Passy’s World
Units for Ratios
The items being compared in a Ratio must always be in the same units.
For example: 1km to 300m needs to be written as 1000m to 300m, which in shorthand form is 1000 : 300
123 days to 1.2 years needs to be converted into 123 days to (1.2 x 365) days = 123 : 438
27 minutes to 2 hours needs to be converted into 27 minutes to (2 x 60) minutes = 27 : 120
Note that we always convert both items into the smaller unit.
(Meters are smaller than kilometers, days are smaller than years, minutes are smaller than hours, and so on).

Image Copyright 2012 by Passy’s World
Related Items
If you enjoyed this post, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our blog, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson valued at $4.99, but 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Ratios Introduction” PowerPoint.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Enjoy,
Passy





Pingback: Simplifying Ratios | Passy's World of Mathematics
Pingback: Finding Ratio Amounts of Proportions | Passy's World of Mathematics
Pingback: Increasing and Decreasing Using Ratios | Passy's World of Mathematics
Pingback: Sharing Using Ratios | Passy's World of Mathematics
Pingback: Similar Triangles | Passy's World of Mathematics