
Image Source: Licence pending from Getty Images
The “Crooked Mile” on the Pillani Highway in Maui Hawaii looks very different to a normal highway !
Volcanic activity and continual movement of the island makes it impossible to build a straight road that will last very long.
Highways are usually made much easier to drive on, by making both sides fo the road follow the exact same straight line direction. We say that the edges of the road are “parallel” to each other.
Highways also need to have the guard rails that run parallel to the surface level of the road, and all line markings also need to be done in parallel.

Image Source: http://constructionfield.net
Parallel Lines are of critical importance when marking out roads, pedestrian crossings, car parks, and airport runways.

Image Source: Home Designer Software
Parallel Lines are also vital on basketball, tennis, volleyball, netball, badminton, and squash courts, as well as on atheletics tracks.
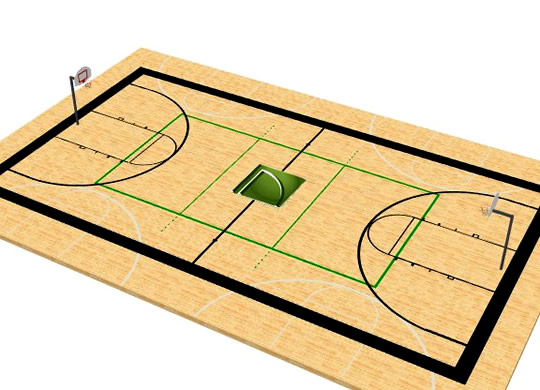
Image Source: Home Designer Software
Parallel Lines are of critical importance in Landscape Design, Timber Deck Work, and Brick work. If all edges are not exactly parallel, then the construction job lacks quality.

Image Source: http://www.felmiatika.com
Train and Tram Tracks need to have rails which run perfectly parallel to each other.

Image Source: http://1.bp.blogspot.com
Electric Power Lines need to run in parallel so that their cables cannot touch each other and short circuit the power grid.
Multi-storey floors and rows of windows in high rise Buildings need to run in parallel.
Sets of Pipes and Cabling in buildings, ships, cars, and aeroplanes are also ran in parallel.
Strings and Frets on guitars and other musical instruments need to run exactly in parallel.

Image Source: Copyright 2010 Passy’s World of ICT
In this lesson we look at the angle properties associated with parallel lines.
Definition of Parallel Lines
Parallel Lines are two or more lines that are always the same distance apart.
We place arrows on the lines to indicate that they are going in the same direction.
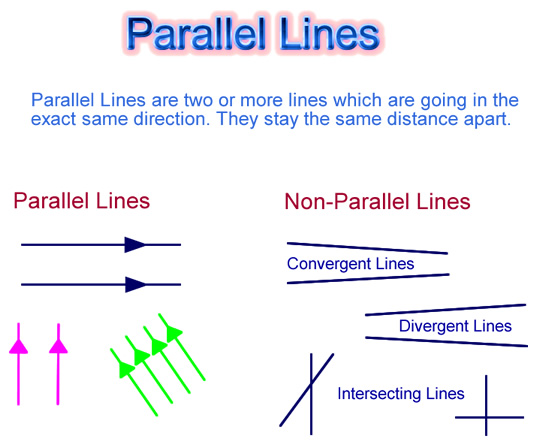
Image Copyright 2012 by Passy’s World
Often with Parallel components, there is also a linear item joining them, which is not at 90 degrees.
This occurs for example in car suspension, where the springs and shock absorbers connect at an angle to their parallel joining components.

Image Source: http://accurate-alignment.com
In Mathematics we draw this diagram as follows, which results in a set of eight angles.
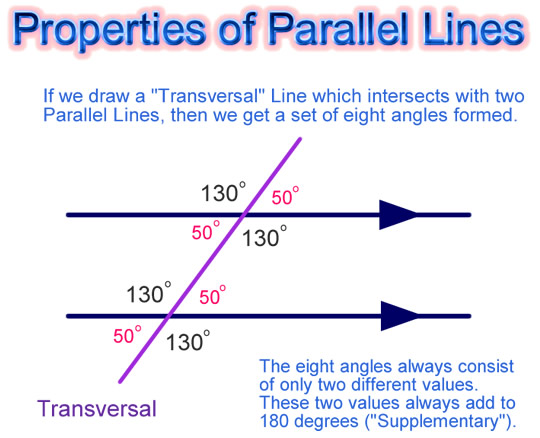
Image Copyright 2012 by Passy’s World
For the set of eight angles there are four common pairings which we use in mathematical Geometry.
These four pairs of Angles are known as:
Vertical “X” Angles
Alternate “Z” Angles
Corresponding “F” Angles
Co-Interior “C” Angles
In the sections which follow, we examine each of these four types of Parallel Lines Angles.
Vertical Angles
These are the pairs of angles which can be found in an “X” shape arrangement in any pair of Parallel Lines that are connected by a Transversal.
These angles are always equal in size to each other.
In mathematics we say they are “Congruent” Angles, because they have exactly the same size and shape.
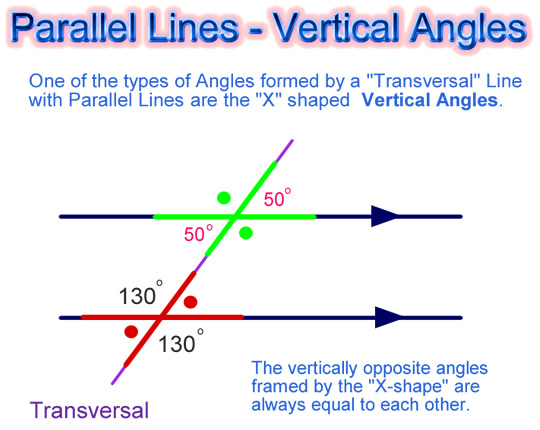
Image Copyright 2012 by Passy’s World
Alternate Angles
These are the pairs of angles which can be found in a “Z” shape arrangement in any pair of Parallel Lines that are connected by a Transversal.
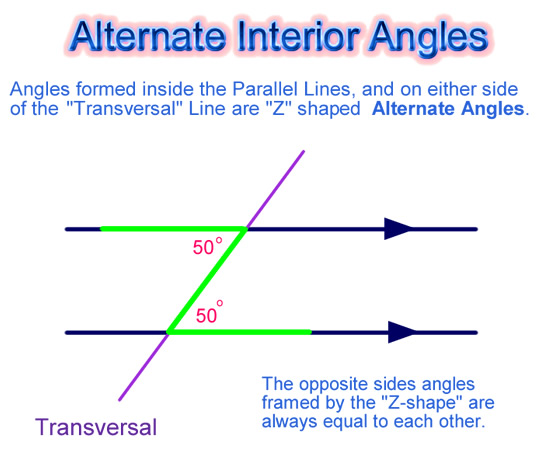
Image Copyright 2012 by Passy’s World
The “Z” shape can also be back to front. Either way around, “Z” type angles are always equal to each other in size.
In mathematics we say they are “Congruent” Angles, because they have exactly the same size and shape.
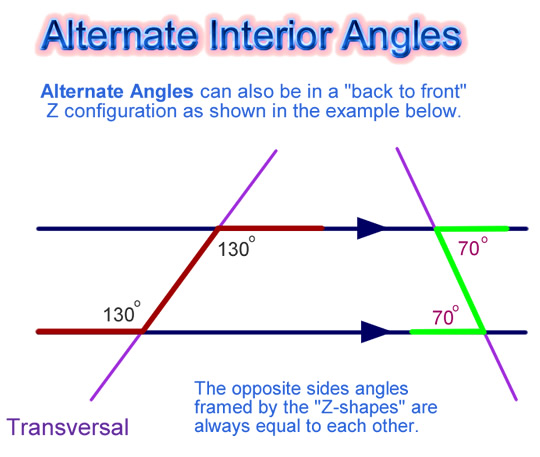
Image Copyright 2012 by Passy’s World
Corresponding Angles
These are the pairs of angles which can be found in an “F” shape arrangement in any pair of Parallel Lines that are connected by a Transversal.
These angles are always equal in size to each other.
In mathematics we say they are “Congruent” Angles, because they have exactly the same size and shape.
Examples of these are shown in the following diagram.
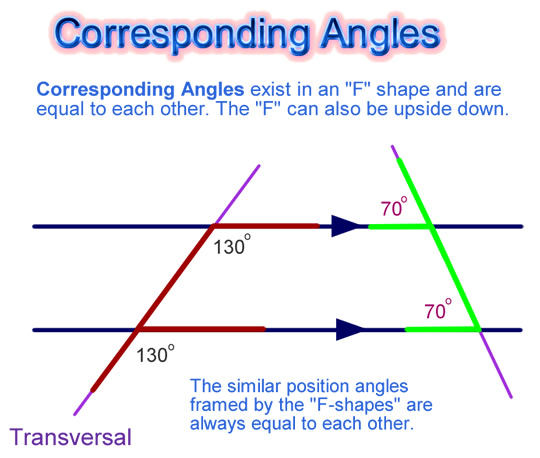
Image Copyright 2012 by Passy’s World
Co-Interior Angles
Unlike Vertical, Alternate, and Corresponding Angles which are equal to each other; Co-Interior Angles are never equal to each other.
Co-Interior Angles exist in a “C” shape and do NOT equal equal each other.
However they always ADD up to equal 180 degrees. Because the sum to be 180, they are “Supplementary Angles”.
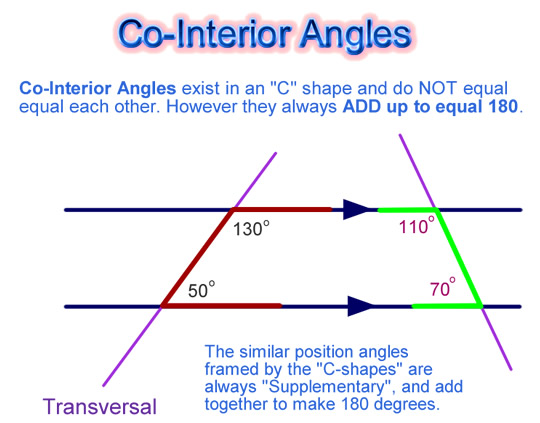
Image Copyright 2012 by Passy’s World
Parallel Lines Videos
The following videos explain the proerties of the following angle types, as well as giving example questions and their solutions.
Vertical “X” Angles, Alternate “Z” Angles, Corresponding “F” Angles and Co-Interior “C” Angles
Vertical Angles Video
Alternate Angles Video
Corresponding Angles Videos
Co-Interior Angles Video
Parallel Lines Summary Video
The following video contains a complete overview of both Parallel and Perpendicular Lines
Examples of Parallel Lines Angles
We can use the Angle Properties of Parallel Lines to solve geometry questions as shown in the following examples.
The steps are basically the same for each question.
– Look carefully at the given angle, and one of the unknown variable angles, and see if they form one of the common patterns such as X-Shape, Z-Shape, F-Shape, and C-Shape.
– Mark the shape onto the parallel lines diagram.
– Use the properties to decide if the unknown angle is equal to the given angle, ( or if “C-Shape” is equal to 180 – the given angle ).
Remember that “C-Shape” angles are the annoying exception where the angles are Supplementary rather than Equal.
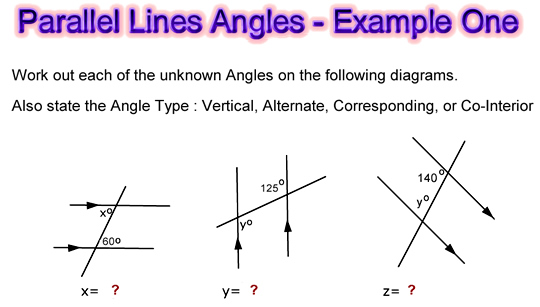
Image Copyright 2012 by Passy’s World
Shown below are the solutions to Example 1.
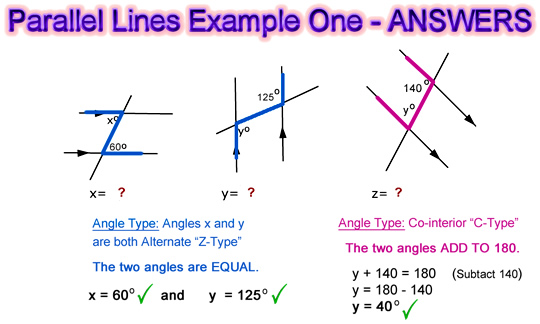
Image Copyright 2012 by Passy’s World
In the next set of examples, we have some Parallel Lines within shapes, and some have more than one relationship to deal with when solving the question.
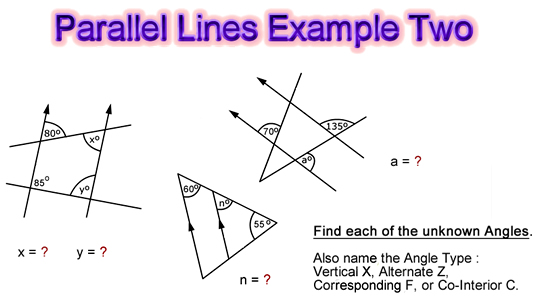
Image Copyright 2012 by Passy’s World
Shown below are the solutions to Example 2.
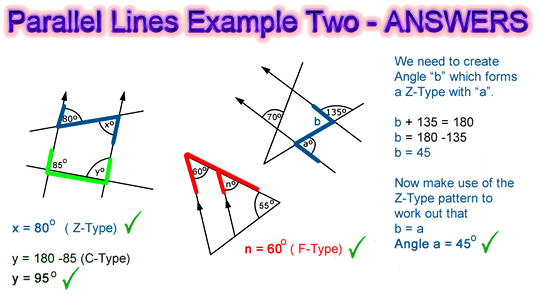
Image Copyright 2012 by Passy’s World
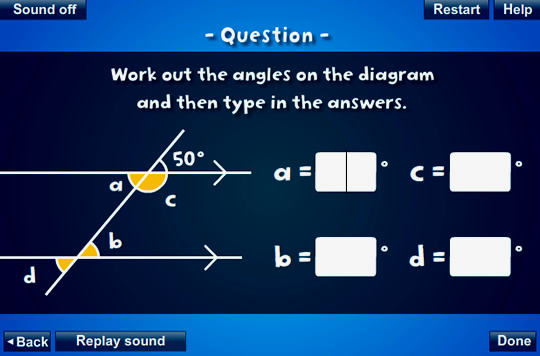
Parallel Lines Online Activity
Watch the animated introduction and then do the online activity by either clicking on the picture or the following link.
http://www.bbc.co.uk/schools/gcsebitesize/maths/geometry/parallellinesact.shtml
Parallel Lines Online Quizes
Do the following quick online quiz that has three parallel lines questions.
The following online quiz from Kahn Academy includes fully worked solutions for each question, and includes Algebra Angle questions.
Click the following link to do this Quiz.
http://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/e
Related Items
Classifying Triangles
Angle Sum in a Triangle
Exterior Angle of a Triangle
GeoGebra
Interactives at Mathwarehouse
Jobs that use Geometry
If you enjoyed this post, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our blog, then please email us at the hotmail address shown in the right hand side bar of this page.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Enjoy,
Passy



Pingback: Isometric Drawing and 3D Cubes | Passy's World of Mathematics
Pingback: Geometry in the Animal Kingdom | Passy's World of Mathematics
Pingback: Jobs With Geometry | Passy's World of Mathematics