
Image Copyright 2012 by Passy’s World of Mathematics
Here at Passy’s World we love playing guitar.
What is really cool is all of the mathematics involved with this amazing instrument.
In this lesson we look at the mathematics associated with the guitar in rock music.
Let’s start with the frets on the guitar neck. We use frets to play specific musical notes.
Pythagoras and Guitar Fret Spacings
Pythagoras was a Greek Mathematician who is famous for his mathematical analysis of the lengths of the sides of right angled triangles.
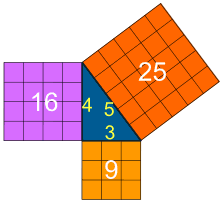
Image Source: http://www.mathsisfun.com
However, Pythagoras worked on a lot of other mathematical ideas, including working out how long guitar strings need to be to create certain notes.
He found that mathematically, the note’s pitch is inversely proportional to the length of the string.
For example if we halve the length of the string, we create the exact same note, but one Octave higher.
This happens on a guitar when we play a note at the 12th fret. Positioning our finger at the 12th fret position, makes the string exactly half as long as its full length with no finger on any frets.
The Inverse Proportion means that if we play 1/2 of the string, we get 2 times the frequency of vibration of the string. This means the musical note gets “twice as big”, making it become the same note, but one octave higher.
Frequency (or how high the note pitch is) increases directly as the length of the string is decreased. This is the fundamental mathematics of all stringed instruments which Pythagoras figured out.
This is shown in the following diagram, along with other key string lengths that are created using the frets on a guitar.
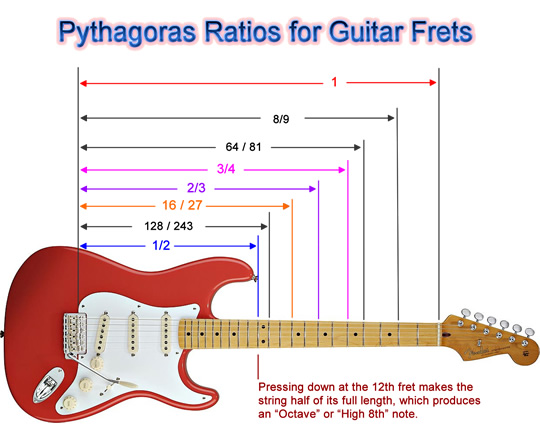
Image Copyright 2012 by Passy’s World of Mathematics
(Click the above picture to enlarge to full screen).
As can be seen in this diagram, Pythagoras worked out in ancient times that using frets to change the string length into certain fractions of the full length, resulted in certain pleasant sounding musical notes.
These Pythagoras fraction values are still used today when making guitars.
There is a great detailed article about Pythagoras and fret spacing on the Noyce Guitar page at the following link:
http://www.noyceguitars.com/Technotes/Articles/T4.html
Ian Noyce is a brilliant guitar maker, (called a “luthier”), right here in Melbourne Australia.
One day I would love to own a Noyce Bass Guitar, as a friend of mine has one, and it feels and sounds absolutely brilliant.
Check out the Noyce Guitar page at this web address:
http://www.noyceguitars.com/index.html
Guitar Notes Mathematics
Here is how the Pythagorean fret positions translate into actual musical notes on the guitar.
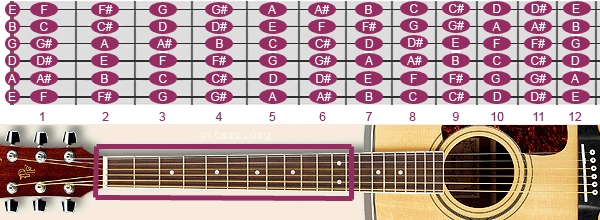
Image Source: http://www.guitar-chord.org
There sure are a lot of notes to memorise!
Thankfully there is a mathematical pattern that we can use to find notes on Guitar Strings.
First we need to assign numerical values to all of the notes in one octave of the Chromatic Scale as follows:

Image Source: http://www.guitarnoise.com
In this mapping the natural notes are A-B-C-D-E-F-G = (0-2-3-5-7-8-10).
If we need to “sharpen” a note, we add 1, and if we need to “flatten” a note, we subtract 1.
The open strings on a guitar have the following numbers: E-A-D-G-B-E = 7-0-5-10-2-7.
To determine the note for any Fret we play on, we add the fret number and the string value to obtain a Total.
We then look this Total up in our Table (that we need to memorize), to work out the note.
For example, on the bottom string E (Note value = 7) then if we are at Fret 3, we do 7 + 3 = 10.
The number 10 in our table is the note “G”.
However, if we do the 7th fret of the bottom E string we get 7 + 7 = 14 which is past the end of our look up table.
Whenever we get a Total Answer greater than 11, we keep subtracting 12 from our Total Answer, until we get a number value between 0 and 11 that we can look up.
For our 7th fret E string example we do 14 – 12 = 2 which is the note “B”.
Working the opposite way, eg. working out the fret number for a note we want to play is a little bit trickier, but can be done.
To find out how, read the excellent article by Bruce Cyburt at the link below:
http://www.guitarnoise.com/lesson/from-math-to-music/
Mathematical Formulas for Frets
There are two Mathematical Formulas for obtaining the correct Pythagoras Fractions for Fret Spacings on the Guitar.
The first rule is commonly called the “Rule of 18”, but the actual value used is 17.817 .
This rule tells us how far the frets need to be apart from each other.
Using this rule we do the string length (from the zero fret “nut” at the top of the guitar to the bridge at the bottom of the guitar) divided by the value of 17.817 and this tells us how far the first fret is from the top “nut” zero fret of the guitar.
Trying this out on one of my own guitars produced 651mm / 17.817 = 36.6mm to the first fret.
To get the position of the second fret we now do (string length – distance to first fret) divided by the value of 17.817 .
This answer is then the distance from the first fret to the second fret.
We keep dividing up the string like this by 17.817 to get all of the fret positions relative to each other.
There is also a mathematical formula which uses powers of 2 in the denominator of the right hand side fraction.
This formula tells us how far each fret needs to be from the bridge at the bottom of the guitar.
This formula works as follows:
dist(x) = s / (2 ^ (x/12) )
where
x = number of the fret being evaluated
dist(x) = distance from bridge at the bottom end of the guitar to fret x on the neck
s = resting string length (distance from the zero fret “nut” at the top of the guitar to the bridge at the bottom of the guitar)
12 = the number of frets per octave that occurs on every Guitar.
This produces the positions for the standard “equal-tempered scale”.
The nut-to-fret positions and fret-to-fret positions are then produced by simple subtractions.
For example, on one of my Guitars the String Resting Length from Bridge to Nut is 651 mm.
If we put in x = 1 for the first fret, and do the calculation, then the answer is 614 mm.
Measuring with a tape measure on my guitar, this is correct, and the distance from the Bridge to the first fret is in fact 614 mm.
Subtracting 651 – 614 gives the distance from the top zero fret “nut” to the first fret to be 37mm.
Again measuring this on my actual guitar showed this 37mm answer to be correct.
Information Source: http://www.musemath.com/miscellany/ruleOf18.html
Vibration of Guitar Strings
The frequency (or size) of a vibrating guitar string depends on the length of the string being plucked, which we create by placing our fingers at various fret positions on the guitar.
These fret positions were originally devised by the ancient Greek Mathematician “Pythagoras”.
As we move further up the fretboard on a given string, we create shorter string length, and therefore higher pitched notes.
Each note on the guitar has a specific frequency of vibration, as shown in the following animated diagram for an E” note on the guitar:
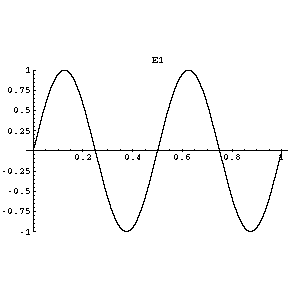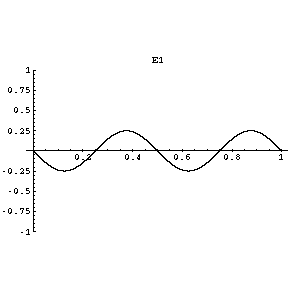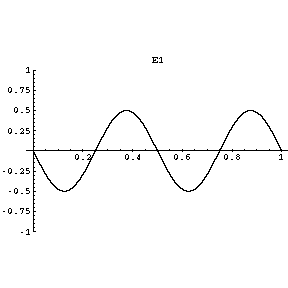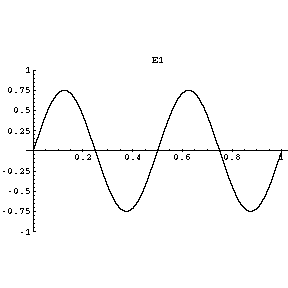
Image Source: http://www.upscale.utoronto.ca
When we bend a string on the guitar, we can make it shift up a note, because we increase the value of the frequency by stretching the string. This is the same thing that happens when we tighten the machine heads to tune a given string.
As well as the main vibration of the string, we also get additional “overtone” sound wave vibrations.
For an “A” note 440 Hz fundamental vibration, the overtones occur at 2 × 440 = 880 Hz, 3 × 440 = 1320 Hz, 4 × 440 = 1760 Hz, 5 × 440 = 2200 Hz, 6 × 440 Hz = 2640 Hz, etc.
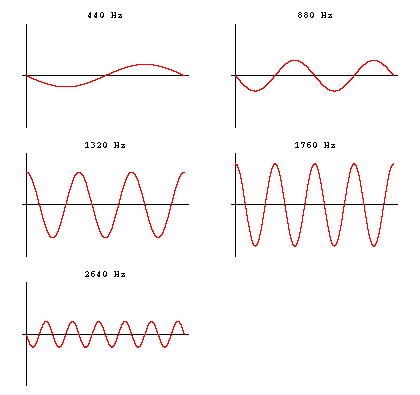
Image Source: http://www.upscale.utoronto.ca
The presence of overtones on any note played on an instrument gives the instrument its “timbre” or distinctive sound.
For example an A note played on a guitar sounds different to an A note played on a violin, due to the differences in overtone instensities.
This mathematics of what sound waves are produced, and in what intensities, makes a Violin sound like a Violin, and a Guitar sound like a Guitar.
For more detailed information on the mathematics of string vibrations, check out the following excellent web page created by David M. Harrison, Department of Physics, University of Toronto in Canada.
http://www.upscale.utoronto.ca/GeneralInterest/Harrison/Vibrations/Vibrations.html
(There is where we obtained the information for this part of the lesson).
Fibonacci Sequence in Music

Image Copyright 2012 by Passy’s World of Mathematics
There is a set of numbers called the “Fibonacci Sequence” which are the values of 1,2,3,5,8 etc; and these values from the most important notes in the musical scale.
A scale is comprised of 8 notes, of which the 5th and 3rd notes create the basic foundation of all chords.
We also have harmonising intervals of 3rds and 5ths.
To produce a “third” we play the first note and a note 2 tones higher than this note.
To play an Octave we play the first note, and then a another note 8 tones higher.
To play a “Power Chord” for rock songs, we play the first note of a chord, and then another note 5 tones higher.
Note in all of the above, (which is the basis of rock music), all of the notes and intervals only use the Fibonacci Numbers 1, 2, 3, 5, and 8.
For more details about the Fibonacci Sequence in Music, click the following link to our separate detailed lesson about this.
http://passyworldofmathematics.com/fibonacci-sequence-in-music/
Octaves – Working in Eights
An Octave is basically the same note played 8 tones higher or lower from where you are currently on the fretboard. The number eight is a Fibonacci Number.
When two notes that are 8 notes apart are played at the same time, it can make a smooth Jazzy sound, or with overdrive, a really cool heavy metal sound.
If you are playing Octaves on Guitar using a pick, then you have to use some of your fingers to mute the strings in between. Depending on the shape you are doing, there might be one or two strings that require muting.
Here are the Octave forms that can be made on the guitar fret board:
One string in between (use a finger to mute this inbetween string, or if playing notes separately, skip this string) :

Image Source: http://www.passyworld.com
Two strings in between Octave forms:

Image Source: http://www.passyworld.com
Here is a video which shows how to use Octaves in Heavy Metal music.
Power Chords – Working in Fifths
Another Fibonacci Number, (apart from the number 8 used for Octaves), is the number 5.
The number 5 is also very important for playing rock guitar.
“Power Chords” are basically 2 or 3 notes that have been taken from a barre chord, and are played as a group on electric guitar, with distortion or overdrive liberally applied.
They are the basis of many rock songs, and musically they are based on 5th intervals.
Eg. We play only the first and fifth note of a chord, where 1 and 5 are both Fibonacci Numbers.
Here is a great eight minute video from YouTube about the basics of Power Chords:
Triplet Notes – Working in Fractions

Image Source: http://www.passyworld.com
A lot of lead guitar soloing involves playing groups of three notes called “Triplets”.
These notes are played to the fraction values of the sound “Trip-o-Let”, and played fast enough to equal the equivalent time of either a quarter note or a sixtennth note.
Since “Trip-o-Let” has eight letters, the shortest note in the group of three syllables is the middle note which is 1/8 th of the Triplet.
The longest note in the triplet is the first note which is 4/8 or 1/2 the length of the triplet.
The final note, or the “Let”, is 3/8.
Knowing these fractions is important if synthesizing music using a Sequencer or Computerised Recorder, as we need to know how to “Quantise” the notes to make them the length of a real triplet.
Triplets are also used on Hi-Hats and other drums when programming drum machines, and so knowing their math is important for drummers as well as guitarists.
For example if we want to produce the sound of a medium speed triplet, then our whole Triplet needs to equal a quarter note.
This means that our “Trip-o-Let” needs to broken up into fractions of 1/4.
The exact time fractions they need to be are as follows:
Trip = 4/8 of 1/4 = 1/2 x 1/4 = 1/8 th.
O = 1/8 of 1/4 = 1/8 x 1/4 = 1/32 nd
Let = 3/8 of 1/4 = 3/8 x 1/4 = 3/32 nd.
To create Triplets on the Guitar, we have to use special playing techniques called “Hammer-Ons” and “Pull-Offs”.
Here is a great video demonstrating the use of Triplets in Guitar soloing.
Mathematics of Songs – Working in Fours
Most Rock songs are played in 4/4 time, where there are four beats to very bar of music.
We then have 4 bar, 8 bar, and 16 bar sections in songs, as well as the classic “12 Bar Blues”.
As can be seen the whole song is based around multiples of four, and this is the heart of rock music, as groups of four are very pleasing to the human ear and brain.
The use of groups of four is essential when using Computer Music Composition Programs such as Apple’s Garage Band, or Magix Music Maker.

Image Source: Screen Capture of Magix Music Maker 15
Mathematical Patterns in Songs

Image Copyright 2012 by Passy’s World of Mathematics
There are a few very common patterns which are used to construct most of the songs that are played on Guitar.
Vocalists need to know these patterns, and be able to count in twos, fours, and eights to know when they need to start singing at the beginning of a song, or after a solo has completed.
Guitarists also need to know the patterns so that they can change from Verse Chords to Chorus Chords, especially after a solo finishes.
Song structures are very mathematical and involve repeating Verses and Choruses one after each other.
One of the most commonly used formulas is the “Verse-Chorus-Bridge” song.
The overall song structure is as follows:
“Verse/Chorus/Verse/Chorus/Bridge/Chorus”
The Bridge is a different musical part to the Verse or Chorus, and can be either a musical solo or some continued vocals.
Another popular song formula is “Verse Chorus” which looks like this:
“Verse/Chorus/Verse/Chorus/Solo/Chorus”
In this song, the Bridge is replaced with a Musical Solo that is played over the top of one or two Verses of music with no vocals.
Less common formulas for songs are ones consisting of just Verses, and no Chorus; as well as the “Verse/Verse/Bridge/Verse” structure.
Jared Leto’s Pythagoras Guitar

Image Source http://www.mcswainguitars.com
Jared Leto is an Actor and also lead singer of the band “30 Seconds to Mars”. One of his guitars is a white guitar called “Pythagoras”.
This guitar was custom made for him by McSwain Guitars who make brilliant customised guitars for a range of famous guitar players such as Slash from Guns and Roses.
Check out McSwain’s awesome Guitars at the following link:
One of Jarred’s band’s best songs is “Closer to the Edge” as featured in the following clip:
Building a “Pythagoras” Guitar Video
There is a lot of mathematics involved with building a guitar. The components need to be precisely measured and fitted to create a good “action” distance of the strings from the fretboard, as well as setting pickup distances, and getting the electronics connected correctly.
The following video is by a guy, who with his father, built a very nice copy of Jared Leto’s “Pythagoras” Guitar.
For those with a technical bent, the specifications for this guitar are as follows:
Seymour Duncan Invader Pickups
Sperzel Locking Tuners
Alder Explorer Neck Through Body
Gracies White Guitar Paint
500K pots
Another excellent video about the making of guitars is this one about the Australian Company: Maton Guitars.
It goes into the Mathematics of the Guitar, and features Ian Noyce talking about Fret Spacings.
Related Items
Fibonacci Sequence in Music
Playing Hammer On Guitar Notes
Playing Pull Off Guitar Notes
Playing Lead Guitar
How to Play Hendrix Hey Joe
How Guitar Pedals Work
Jazzy Guitar Octaves
Guitar Arpeggios
Playing Guitar Power Chords
Magix Music Maker
Adjusting Electric Guitars
Computer Enhanced Music
V-Guitar Free Online Lessons
If you enjoyed this post, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our blog, then please email us at the hotmail address shown in the right hand side bar of this page.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Like Us on Facebook
Our Facebook page has many additional items which are not posted to this website.
These include items of mathematical interest, funny math pictures and cartoons, as well as occassional glimpses into the personal life of “Passy”.
Check it out at the following link:
https://www.facebook.com/PassysWorldOfMathematics
While you are there, LIKE the page so you can receive our FB updates to your Facebook News Feed.
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy



Pingback: Mathematics of the Melbourne Cup | Passy's World of Mathematics
Pingback: The Cosine Ratio | Passy's World of Mathematics