
Image Source: http://www.juicing-for-health.com
In a previous lesson we showed how to Solve Equations using the work down through the “Onion Skins” Method.
Knowledge of that lesson is needed as a background, before doing our lesson on Rearranging Formulas.
Click here for Onion Skins Equations Lesson
In our Transposing Formulas lesson we will review the use of the “Onion Skin” method, and show how it can be applied to Transposing (or rearranging) Algebra Formula Equations.
Review of Onion Skin Method
Here are the steps that we follow to solve an Equation using Onion Skins.

Image Copyright 2013 by Passy’s World of Mathematics
Here is an example of solving a simple Equation using the Onion Method.
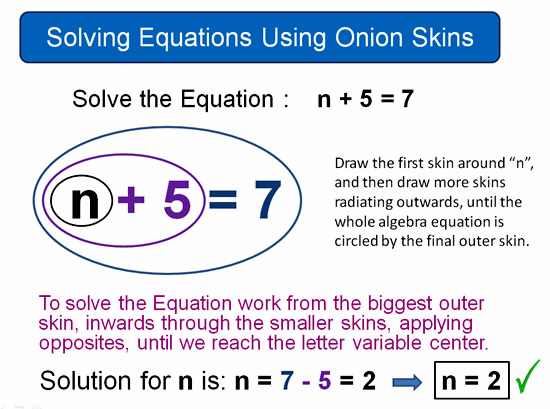
Image Copyright 2013 by Passy’s World of Mathematics
Onion Skins for Transposing
The steps we do for Transposing an Equation into a new equation with a different letter variable as the subject, is basically the same as we do for Solving Equations.
Transposing Equations is the same as Solving Equations, except that we have a set of letter variables to deal with, and very few if any numbers present.
Here is a simple Transposing Example that is very similar to our previous Solving Equation example.
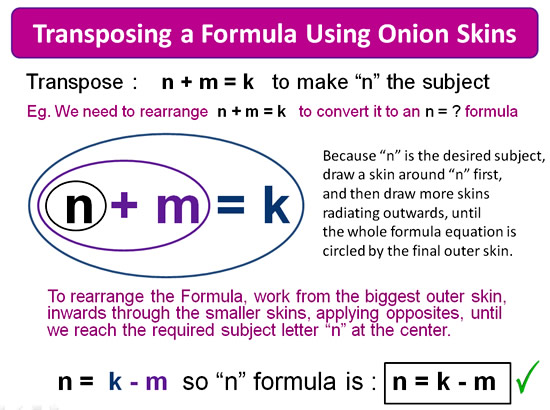
Image Copyright 2013 by Passy’s World of Mathematics
Solving a Two Step Equation Using Onion Skins
The following example shows how to solve a two step equation.
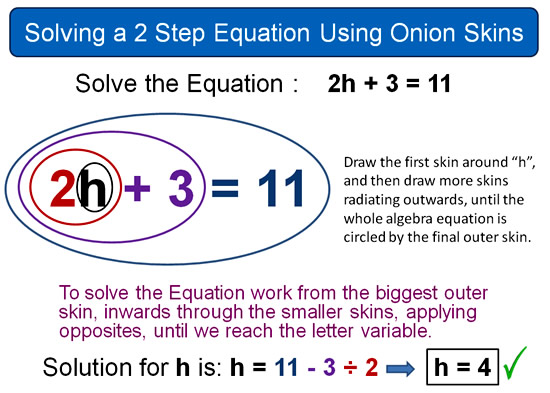
Image Copyright 2013 by Passy’s World of Mathematics
We always put our first innermost circle around the letter variable we are solving for, in this case it was “h”.
In the above example, the variable letter “h” is x2 and +3.
If you are not sure which of these two operations gets circled first, remember we have to do them in BODMAS/PEMDAS order.
This means we circle the 2h for x2 before we circle the 2h + 3 for the +3 operation.
Transposing a Two Step Formula Using Onion Skins
Let’s now look at a Formula that is very similar to the Equation we just solved, but contains lots of letters instead of numbers.

Image Copyright 2013 by Passy’s World of Mathematics
Formulas Containing Exponents and Fractions
The following examples show to transpose formulas that contain exponents such as power of 2 squares.
Squaring comes under the “O” for other things in BODMAS, and under the “E” for Exponents in PEMDAS.
Because it is the next operation to follow brackets, it is usually one of the very first onion skins we draw around our letter.
Square Root is the opposite of Squaring, and so when we peel the Onion we do square root to undo squaring.

Image Copyright 2013 by Passy’s World of Mathematics
The next example contains a Square power of 2 exponent, but because it is not on the letter we are transposing to, we do not have to reverse it out with a square root.
The formula has a Fraction and we need to move it into the bottom of our Algebra Formula BEFORE we draw our Onion Skins.
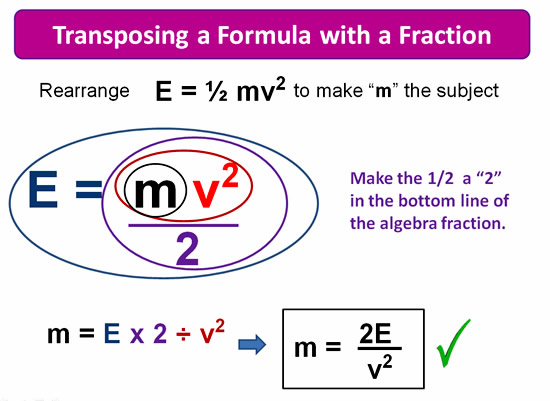
Image Copyright 2013 by Passy’s World of Mathematics
In the next example, we are using the same formula, but this time we are transposing to make “v” the subject.
This “v” that we are transposing to does have a square on it, so we will have to do a square root reversal of it when we “peel” our onion.
(Squaring and Square Roots are opposites, just like + and – are opposites).
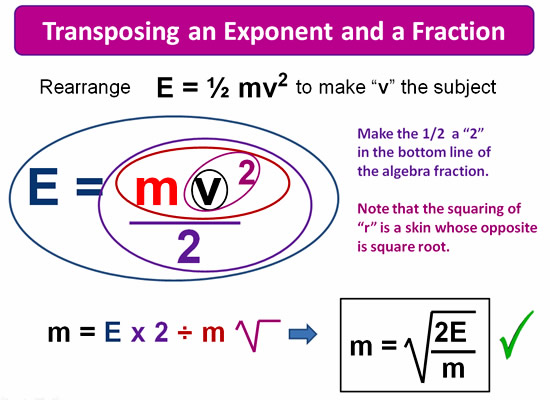
Image Copyright 2013 by Passy’s World of Mathematics
Transposing Financial Mathematics Formulas
Financial Mathematics has a lot of Cost Price, Selling Price, Markup, Discount, Profit and Loss Formulas.
Rather than memorising every single possible formula we may need, it is much easier to only know the main formulas, and then be able to transpose these to get any other formulas we need.
In the following example, we start with the Formula for applying a discount “D”, to a Marked Price on an item “M” to work out the selling price “S”.
We transpose the formula to an M= formula, so that we could work out the original Marked Price required on an item if it is going to sell for a certain amount when discounted.
Notice that we follow “BODMAS/PEMDAS” order, and onion circle the brackets item before circling the dividing part of the formula.
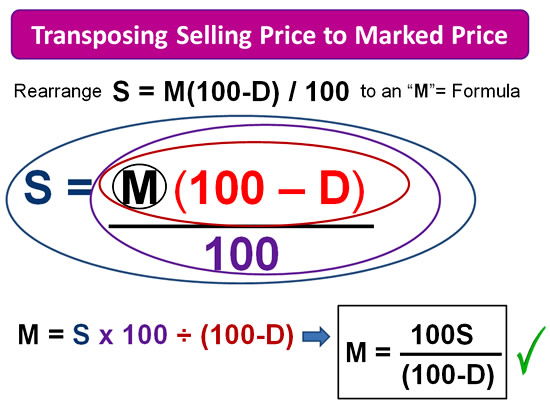
Image Copyright 2013 by Passy’s World of Mathematics
Transposing a Multi-Variable Formula
In this next example we have quite an involved formula, which results in many onion skins that have been drawn outwards from our subject letter of “c”, in BODMAS/PEMDAS order.
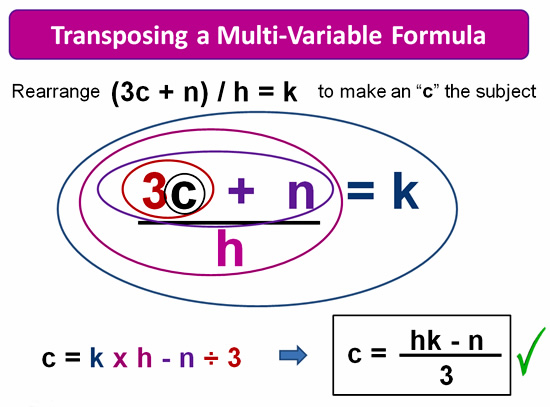
Image Copyright 2013 by Passy’s World of Mathematics
Transposing a Square Root Formula
The following formula contains a square root, and when we reverse this out in the peeling process we use squaring as its opposite.
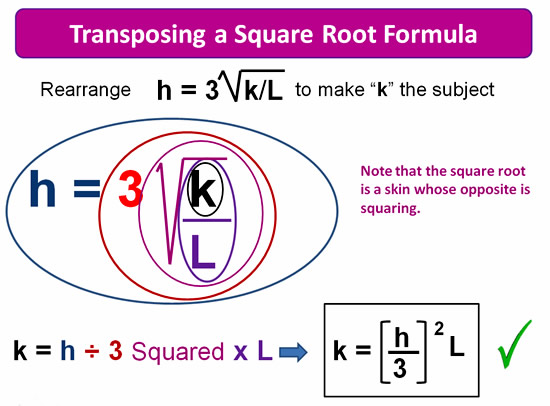
Image Copyright 2013 by Passy’s World of Mathematics
The above transposing is probably the most complicated example we have covered.
Note that because the k/l is all under the Square Root sign it is circled before the actual Square Root sign.
This does not seem to follow BODMAS/PEMDAS, because the “D” dividing should come after the “O” other things square root.
The k/l being under the Square Root sign is kind of like it being in brackets, and it must be considered first, before a Square root can be taken.
Eg. Square Root of 27/3 would be worked out as Square Root of 27/3 = Square Root of 9 = 3; and not as Square Root of 27 then divided by 3.
Transposing When Subject is in Denominator
If our desired subject letter varibale is inthe bottom of a Fraction, we cannot directly apply the onion skins.
We must first flip over both sides of the Equation, and then do our Onion Skins.
This is mathematically Possible because things like 12/6 = 6/3 are still true when we flip both sides and have 6/12 = 3/6.
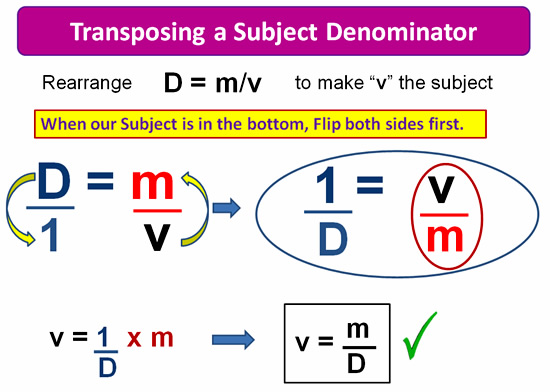
Image Copyright 2013 by Passy’s World of Mathematics
Related Items
Solving Equations Using Onion Skins
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Transposing Formulas Using Onion Skins” Powerpoint.
Like Us on Facebook
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy




