Similar Triangles turn up in the strangest of places, even in Jewellery made from crystals of the gem stone “Tourmaline”.

Images Sourced from Google Images
In this lesson we look at the nature of similar figures, concentrating on Similar Triangles.
Similar objects have the exact same shape but are different in size.
We cover the methods and rules for establishing similarity.
We also work out how to find unknown sides using Similarity Ratios.
If you are not sure about Ratios, we suggest a review of these previous lessons:
http://passyworldofmathematics.com/introduction-to-ratios/
http://passyworldofmathematics.com/finding-ratio-amounts-of-proportions/
We highly recommend that you have also done our Congruent Triangles lesson, before doing Similar Triangles.
http://passyworldofmathematics.com/congruent-triangles/
In the Similar Triangles lesson here, we do not cover composite similar triangle questions, or applications of Similar Triangles, as these are covered in a separate lesson.
Similar Objects
Two or more items are similar to each other if they have the same shape, but are different sizes.
SIMILAR = SAME SHAPE, DIFFERENT SIZE

Image Copyright 2013 by Passy’s World of Mathematics
Scale Factor
The amount by which we increase, or decrease, the size of an object is called the “Scale Factor” or “S.F.”
The following examples of enlarging and reducing the size of a photo illustrate the concept of Scale Factor.

Image Copyright 2013 by Passy’s World of Mathematics

Image Copyright 2013 by Passy’s World of Mathematics
Calculating the Scale Factor
We calculate the SCALE FACTOR by comparing matching sides, using Ratios.

Image Copyright 2013 by Passy’s World of Mathematics
The following video gives a good introduction to Scale Factor, and also shows some real world applications that involve using Ratio Fractions and Cross Multiplying.
If you are not sure about Ratios, and the Cross Multiplication Method, then check out our previous lesson on this at the link below:
http://passyworldofmathematics.com/finding-ratio-amounts-of-proportions/
Checking for Similar Objects
For two objects to be similar, all their measurements must be changed in the exact same Ratio.
The two objects will then be proportional to each other.
In the example below we first enlarge a 4:3 aspect ratio photo to be double its original size.
The beginning small photo, and the ending larger photo are the exact same shape, and are similar objects.
In the second photo enlargement in our example, we have changed from Standard digital camera 4:3 ratio, to Wide Angle 16:9 aspect ratio.
When we do the ratio proportion mathematics, we find that the ratios of the corresponding sides are NOT the same.
In this 4:3 to 16:9 enlargement, we do not have the same shape, we now have a much wider photo, and so the two photos are NOT Similar.

Image Copyright 2013 by Passy’s World of Mathematics
Similar Triangles
Similar Triangles are the exact Same Shape, but are Different Sizes.
In the remainder of this lesson we will be looking at Similar Triangles.
The following example of two similar triangles involves one triangle, and then a second half size copy of the triangle.
For any two similar triangles their angles will be identical.
However, the sides of the second triangle will be either an Enlargement or a Reduction of the sides of the first triangle.

Image Copyright 2013 by Passy’s World of Mathematics
Introductory Video on Similar Triangles
The following video gives a good introduction to Similar Triangles, including some proofs and problem solving.
Determining Similar Triangles
Similar Triangles need to have the exact same shape, which will happen when their angles are all the same.
Similar Triangles are NOT the same size, which means that their matching sides are NOT equal.
Instead their matching sides are “In Proportion”, eg. either Enlarged or Reduced.
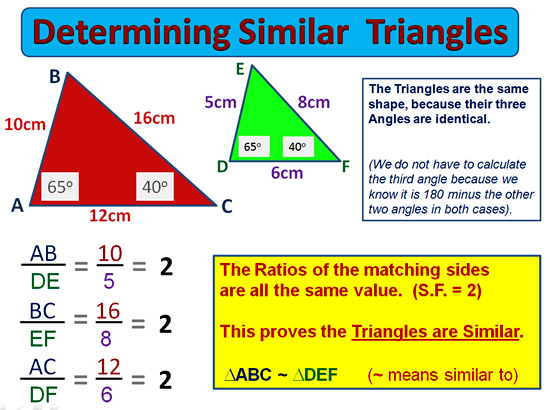
Image Copyright 2013 by Passy’s World of Mathematics
Similar Triangle Rules
Like was the case for Congruent Triangles, there are some “shortcut” rules we can use to prove that two triangles are similar.
Eg. We do not have to check that all three angles are equal, or that all three sides are in proportion.
The shortcut Rules for working out if two triangles are similar to each other are a lot like the rules we use for Congruent Triangles.
There are four Rules for Similar Triangles:
Angle Angle Angle or “AAA”, which turns out to really be just the Angle Angle or “AA” Rule
Proportional Side, Proportional Side, Proportional Side or “PPP” or “SSS” Rule
Proportional Sides, Equal Included Angle, Proportional Sides or “PAP” or “SAS” Rule
Right Angle, Proportional Hypotenuses, Proportional Sides or “RHS” Rule.
Here are some summaries of those four rules.
Angle Angle Angle AAA Rule
If all three Angles are the exact same sizes, (but sizes of triangles are different), then the triangles must be similar.
We actually only need two pairs of matching angles the same, because the third pair will automatically match, because the total angle size in any triangle adds up to 180 degrees.
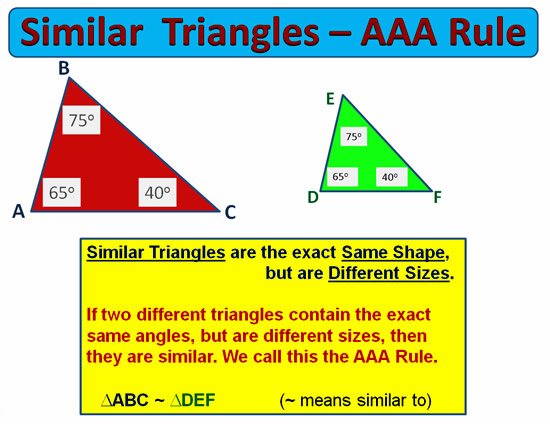
Image Copyright 2013 by Passy’s World of Mathematics
Proportional Sides PPP or SSS Rule
Here at Passy’s World we like to call this the “PPP” rule, rather than the “SSS” Rule, and leave the “SSS” Rule as being for Congruent equal sized triangles only.
The “PPP” Rule is true if all three sides of the two triangles produce the same Scale Factor value.
If all three sides have the same S.F. then the sides are all in proportion and the two triangles are similar.
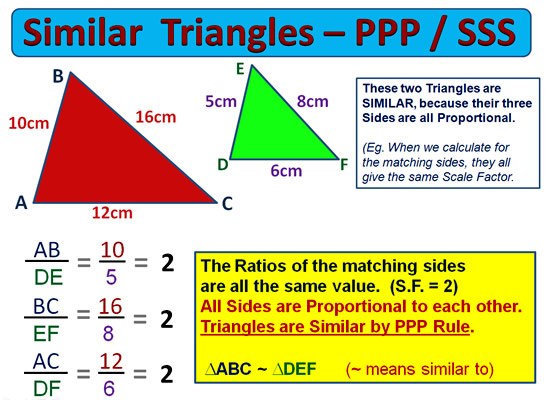
Image Copyright 2013 by Passy’s World of Mathematics
Proportional Sides with Angle PAP or SAS Rule
We prefer to call this the “PAP” rule, rather than the “SAS” Rule, and leave the “SAS” Rule as being for Congruent equal sized triangles only.
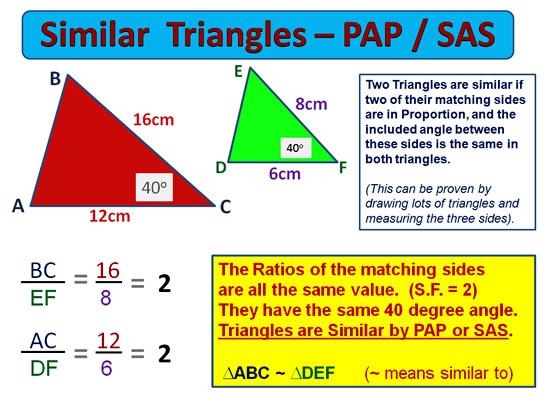
Image Copyright 2013 by Passy’s World of Mathematics
Right Angled Triangles RHS Rule
This rule is a lot like the RHS rule for congruent equal sized triangles.
However, in this similar triangles rule, the hypotenuses and either pair of the two sides are in Proportion to each other, rather than being equal to each other.
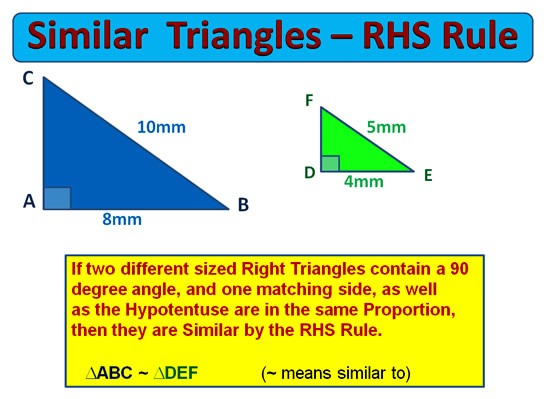
Image Copyright 2013 by Passy’s World of Mathematics
Video About Triangles Rules
The following video covers the four Similar Triangles Rules
Similar Triangles in the Real World
Similar Triangles can be found in Nature, in Art and Craft, and in many structures we design and build.
Amazing Similar Triangles are found inside the crystals of the beautifully colored “Tourmaline” gemstone.

Image Copyright 2013 by Passy’s World of Mathematics

Image Copyright 2013 by Passy’s World of Mathematics
Similar Triangles can create striking effects when used in Art and Craft.

Image Copyright 2013 by Passy’s World of Mathematics

Image Copyright 2013 by Passy’s World of Mathematics
Similar Triangles provide reinforced strength and rigidity to structures, as well as greatly reducing the weight of the objects they are used in.

Image Copyright 2013 by Passy’s World of Mathematics
Examples of Using Similar Triangle Rules
In this first example, we are asked to use either AAA or PPP or PAP or RHS to prove that we have Similar Triangles.
It turns out we need to use the “AAA” Rule.
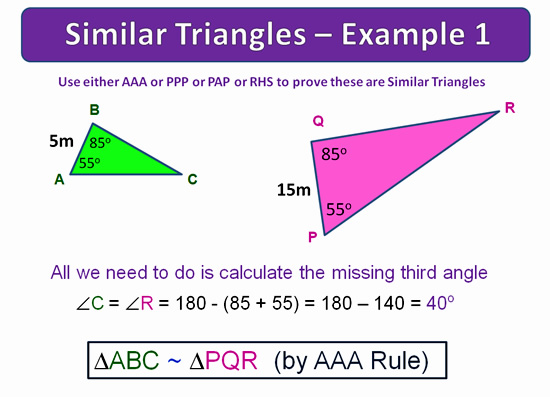
Image Copyright 2013 by Passy’s World of Mathematics
In this second example, we are asked to use either AAA or PPP or PAP or RHS to prove that we have Similar Triangles.
The two triangles have two sides and the included Angles inbetween these two sides.
Therefore we need to used the PAP / SAS Rule.
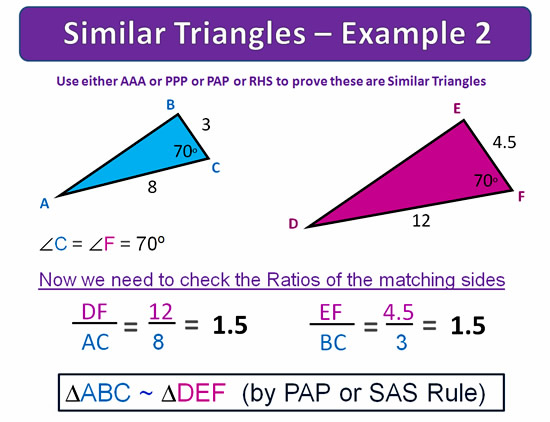
Image Copyright 2013 by Passy’s World of Mathematics
Examples of Solving Similar Triangles
In this first Example, we need to first prove that the Two Trianges are Similar.
After this we can find the Scale Factor that exists between the two tiangles.
Using the S.F. value, we then find the unknown side.
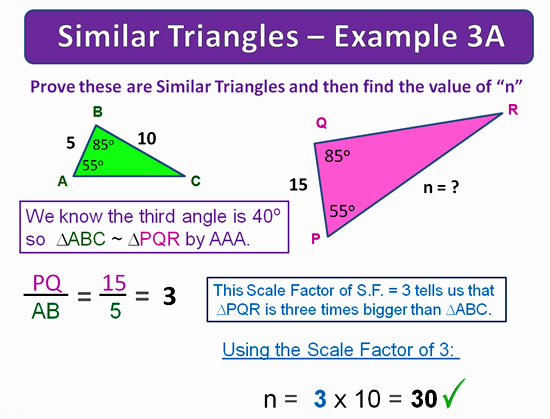
Image Copyright 2013 by Passy’s World of Mathematics
Using the Scale Factor works well for situation where we have the known side on a small triangle, and we need to find the unknown length of the matching side on a big triangle.
However, if the situation if the other way around, we get fraction Scale Factors such as one third 1/3 to deal with and this makes the mathematical working out a bit fiddly.
Another way to solve similar triangles is to write two rations and then use “cross multiplying”, (or “Cross Products”).
At Passy’s World we prefer to use this “Cross Products” method for solving triangle questions, because it helps avoid dealing with fractions.
In “Example 3B” below, we redo “Example 3A”, but this time use the Cross Products Method to solve our triangle question.
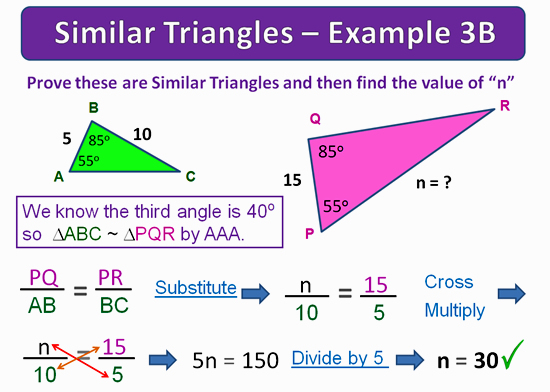
Image Copyright 2013 by Passy’s World of Mathematics
In this final “Example 3C” our question is the other way around, and we have to find an unknown side on the smaller triangle.
We could work out that the Scale Fator is 10/30 and reduce this down to 1/3. But then we get into fractions work to get to the final answer.
Here at Passy’s World, we have found that students have difficulty with fractions, and so we have worked out “Example 3C” using Cross Multiplyling as shown below.
Using Cross Multiplying avoids having to deal with fractions, and we believe that is a good thing.
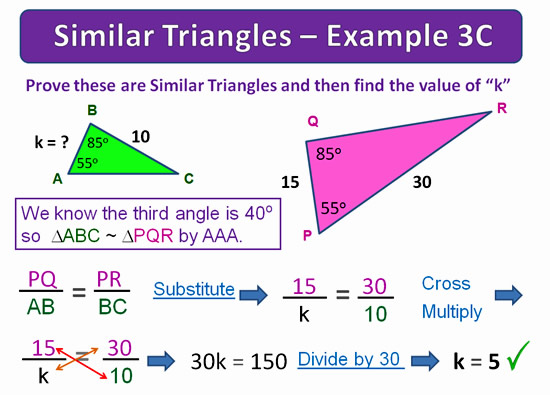
Image Copyright 2013 by Passy’s World of Mathematics
Videos About Solving Similar Triangles
Here are some videos where unknown sides are found for Similar Triangles
Similarity concepts can also be applied to Quadrilaterals as well as Trinagles.
This is demonstrated very well in the following video by Mr Bill Konst.
Music Video About Similar Triangles
Here is a bit of a humorous rap song about Similar Triangles.
There are some extremely, but a bit way out, mathematical concepts related to triangles covered in this entertaining little story.
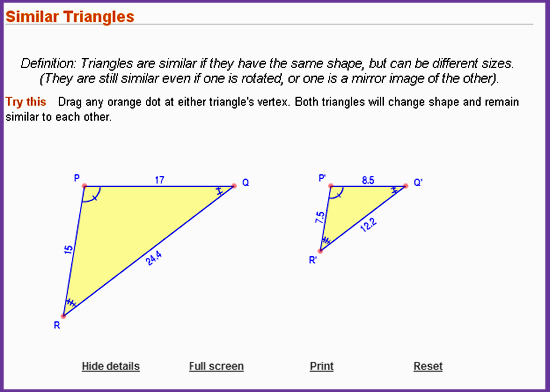
Interactive Similar Triangles
The above Online Manipulative, (which can go full screen), allows us to drag corner vertices around and make any kind of shaped pair of similar triangles.
Click the link below to try it out:
http://www.mathopenref.com/similartriangles.html
Related Items
Classifying Triangles
Angle Sum in a Triangle
Exterior Angle of a Triangle
Angles and Parallel Lines
Congruent Triangles
Pythagoras and Right Triangles
Jobs that use Geometry
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Similar Triangles – Part 1” Powerpoint.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Like Us on Facebook
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy






Pingback: Geometry in the Animal Kingdom | Passy's World of Mathematics
Pingback: Similar Triangles Applications | Passy's World of Mathematics
Pingback: Jobs With Geometry | Passy's World of Mathematics
Pingback: Trigonometry – Labeling Triangles | Passy's World of Mathematics
Pingback: The Sine Ratio | Passy's World of Mathematics
Pingback: The Cosine Ratio | Passy's World of Mathematics
Pingback: Trigonometric Ratios | Passy's World of Mathematics