
Image Source: http://rekkerd.org
In this lesson we are doing some more Trigonometry.
Shown above are some basic “sinusoidal” shaped sound waves.
Our ear detects these when music is played.
Various “Guitar Pedals” or “Stomp Boxes” can be used to modify these basic sound waves to create new and interesting sounds.
The mathematics of these curve shaped waves involves the trigonometry of right angled triangles.
These curved shaped waves are formed by graphing all of the decimal trigonometry values which can be formed by different shaped right angled triangles.
This is illustrated very nicely by the following diagram:
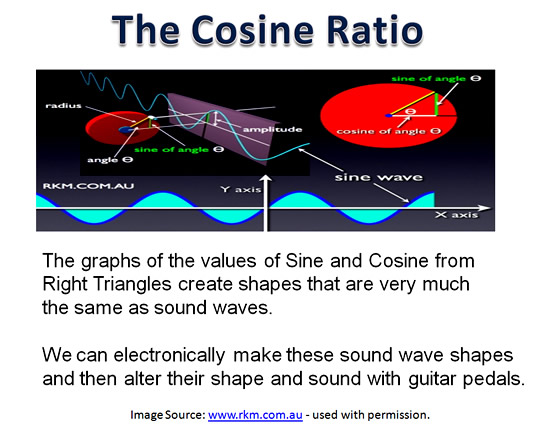
Image used with Permission from Russell Kightley
Distorted Heavy guitar sound occurs when smooth Sine Waves are mathematically transformed into Square shaped, Sawtooth, and Triangle shaped waves.
This is shown in the animation below:
The mathematics of wave re-shaping works to create a wide variety of electric guitar sounds.
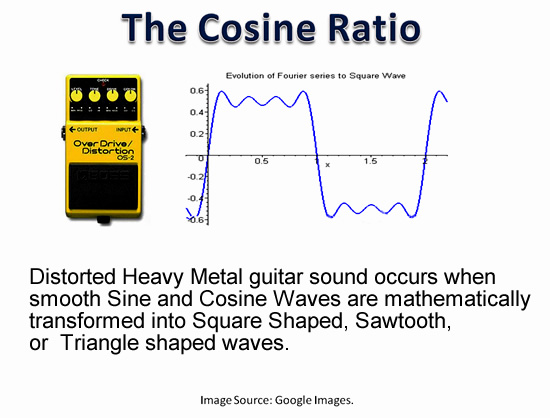
Image Copyright 2013 by Passy’s World of Mathematics
Guitar Mathematics

Image Copyright 2013 by Passy’s World of Mathematics
Here at Passy’s World we love playing Guitar.
If you would like to find out more about the Mathematics of the Guitar, then check out our lesson on this at the following link:
http://passyworldofmathematics.com/guitar-mathematics/
Trigonometry is extremely important in areas involving waves such as Sound, Light, Electricity, and Oceanography.
In this lesson we look at the trigonometry function known as “Cosine”.
The Cosine Ratio
There are three main Trigonometry Ratios: Sine, Cosine, and Tangent.
It is difficult to try and learn all three of these at once, and so this lesson only covers the Cosine Ratio.
At Passy’s World, we have found that trying to learn all three Ratios at once, is like trying to learn how to Drive, Chip, and Putt, all in one Golf Lesson.
It is difficult, confusing, and frustrating.
We prefer to learn the Sine Ratio, and then the Cosine Ratio separately, before trying to deal with all three Trig Ratios.
Before doing this lesson on Cosine Ratios, it is important that you know how to label the sides of a Right Triangle as “Hypotenuse”, “Opposite”, and “Adjacent”.
If you need to learn how to label a Right Triangle, then click the link below:
http://passyworldofmathematics.com/the-sine-ratio/
It is also important that you have already studied the Sine Ratio in our previous lessone at the link below:
http://passyworldofmathematics.com/trigonometry-labeling-triangles/
The Cosine Ratio involves the Adjacent and Hypotenuse sides of a Right Triangle as follows:

Image Copyright 2013 by Passy’s World of Mathematics
The Cosine Ratio will be the same for any Right Triangle which has a particular Angle value contained in it.
The diagram below show this for three different sized 37 degree Right Triangles.
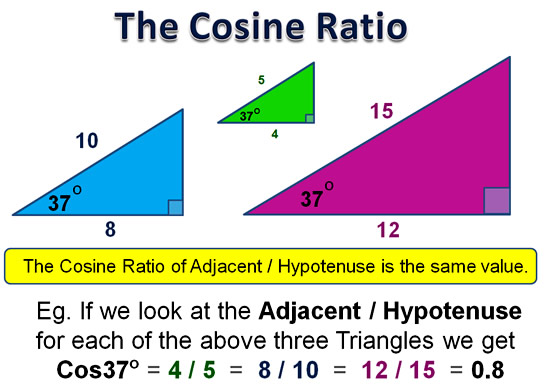
Image Copyright 2013 by Passy’s World of Mathematics
Cosine Triangle – Formulas Summary
Here are the four formulas we use when working with Cosine Triangles.

Image Copyright 2013 by Passy’s World of Mathematics
Using the Calculator for Cosine Triangles
If we are given an angle and we need to determine its decimal Cosine value, we can do this on a Calculator as shown below:
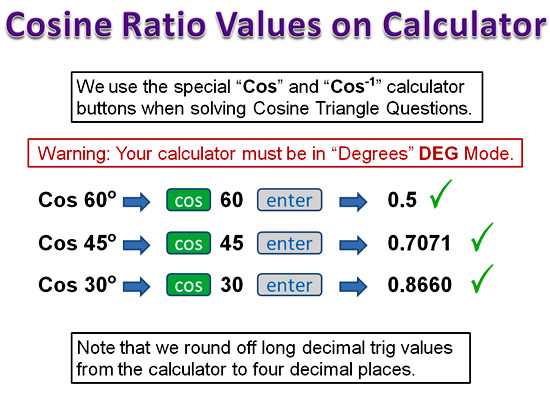
Image Copyright 2013 by Passy’s World of Mathematics
If we are given an Adjacent and a Hypotenuse, and we need to determine the reference Angle value, we can do this on a Calculator as shown below:
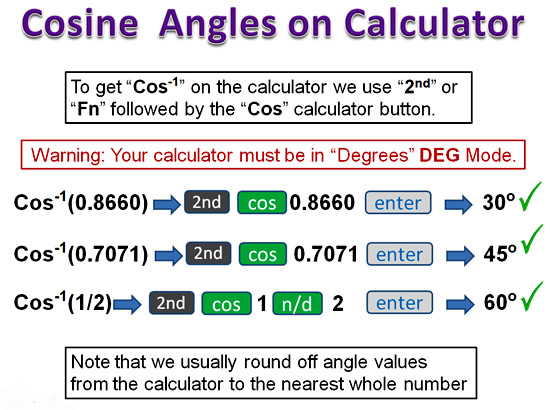
Image Copyright 2013 by Passy’s World of Mathematics
The above function is sometimes also called finding the “ArcCos” or the “ACos”.
Online Trigonometry Calculator
If you would like to use an online calculator to find “Cos” or Angle values, then there is one at the following link:
Note that you will need to set this calculator to 4 decimal places for Sin values.
Cosine Triangle – Working Out Steps
If we are working on a right triangle which involves an Adjacent and a Hypotenuse, then here are the steps we need to follow.

Image Copyright 2013 by Passy’s World of Mathematics
Follow the above steps for doing all questions for Cosine Triangles.
Cosine Triangle Examples
The following examples show how we apply our Cosine Triangle formulas to questions to work out unknown values on Right Triangles.
In this first example we are asked to find the value of the “Adjacent” side.
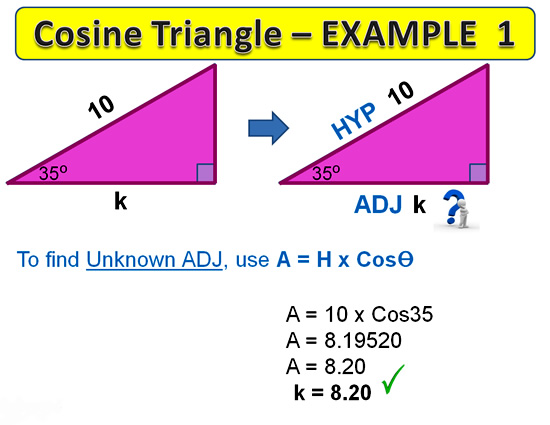
Image Copyright 2013 by Passy’s World of Mathematics
The next example shows how to find the value of the “Hypotenuse” for a Cosine Triangle.

Image Copyright 2013 by Passy’s World of Mathematics
In our next example we use the Inverse Cosine function to find an unknown Angle.
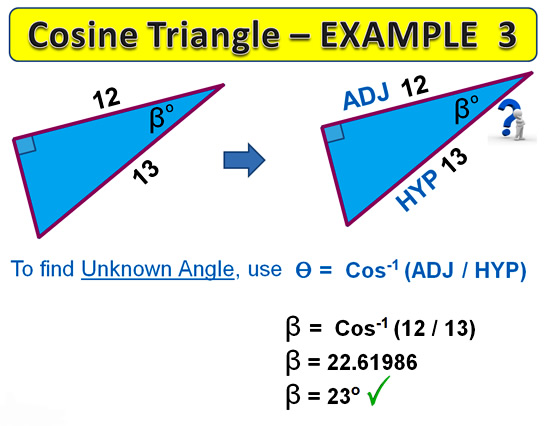
Image Copyright 2013 by Passy’s World of Mathematics
In this final example, we are given the Adjacent and Hypotenuse, and asked to fine the decimal value of Cosine.
It is important to read questions carefully, and not immediately assume that this is a Find the Angle example, like Example 3.
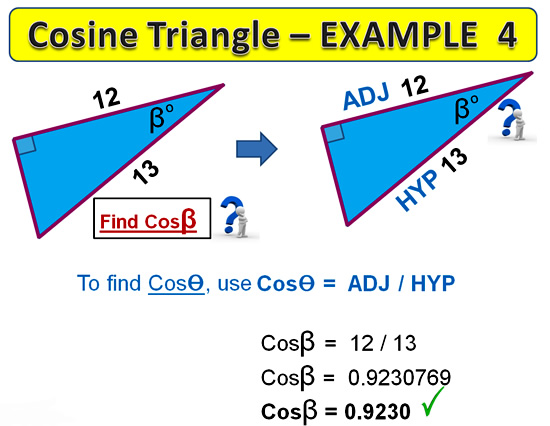
Image Copyright 2013 by Passy’s World of Mathematics
Cosine Ratio Worksheet
The following worksheet contains several type of Cosine Ratio questions, and includes Answers at the end of the sheet.
Click the following link to access this Cosine Ratio worksheet:
Related Items
The Sine Ratio
Labeling Trigonometry Triangles
Trigonometric Ratios – Sin Cos and Tan
Classifying Triangles
Pythagoras and Right Triangles
Congruent Triangles
Tall Buildings and Large Dams
Similar Shapes and Similar Triangles
Geometry in the Animal Kingdom
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “The Cosine Ratio” Powerpoint.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Like Us on Facebook
Our Facebook page has many additional items which are not posted to this website.
These include items of mathematical interest, funny math pictures and cartoons, as well as occassional glimpses into the personal life of “Passy”.
Check it out at the following link:
https://www.facebook.com/PassysWorldOfMathematics
While you are there, LIKE the page so you can receive our FB updates to your Facebook News Feed.
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy








Pingback: The Tangent Ratio | Passy's World of Mathematics