Image Source: Photo by Jeff Wilson – www.warbirddepot.com
Trigonometry is used a lot in the work done by Pilots and Air Traffic Controllers.
However, a lot of the maths formulas are programmed into computer applications, and we do not see people sitting around pushing the sin, cos and tan buttons on calculators!
In this lesson we look at the Tangent Ratio.

Original Plane Photo by Geoff Wilson
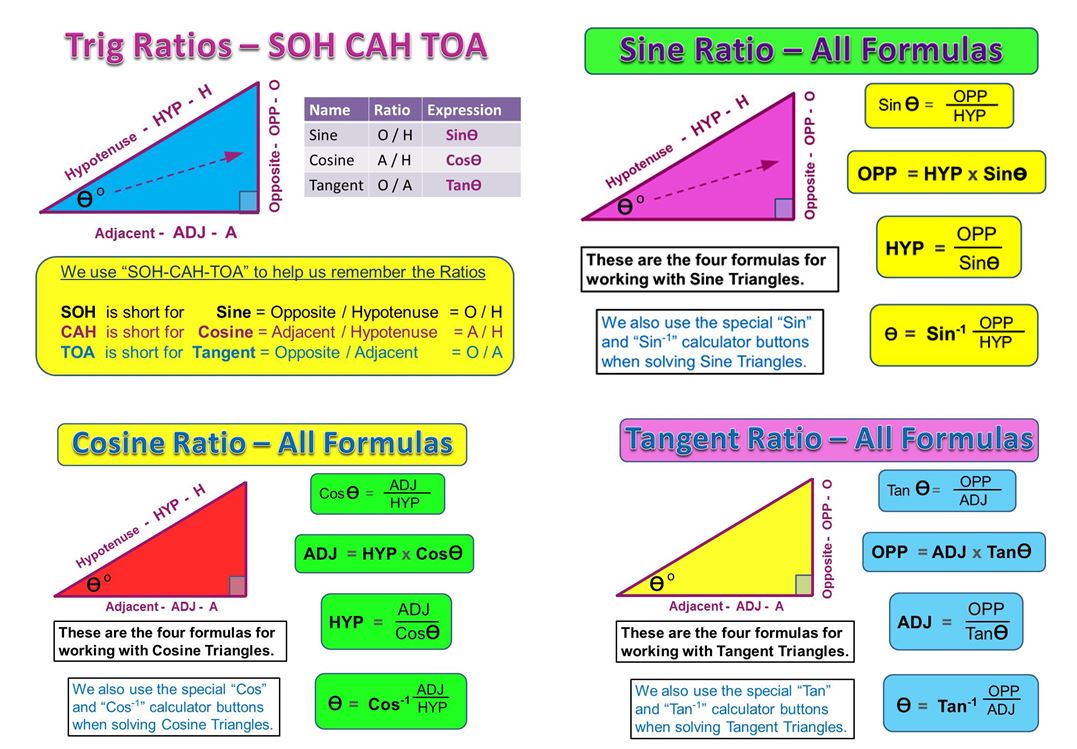
Definition of the Tangent Ratio
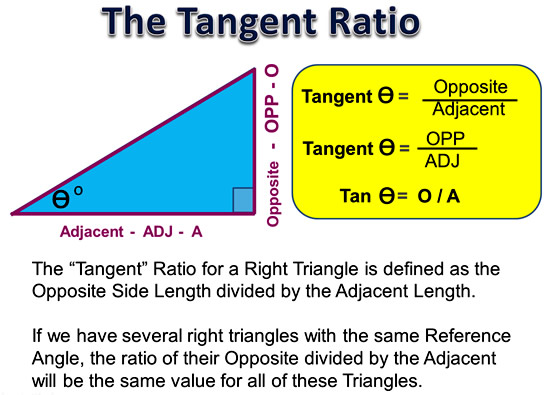
Image Copyright 2013 by Passy’s World of Mathematics
Like other Trig Ratios, the Tan Ratio works out the same value for any sized triangle that has the same Reference Angle in it.
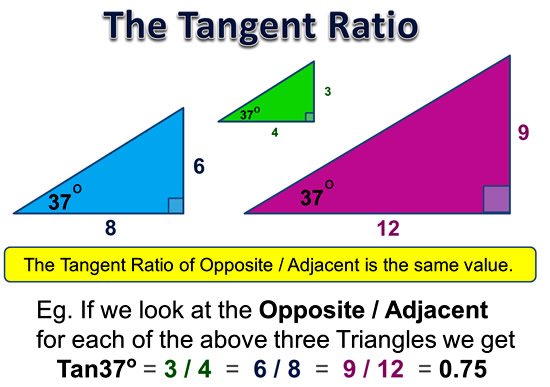
Image Copyright 2013 by Passy’s World of Mathematics
Tangent Formulas Summary

Image Copyright 2013 by Passy’s World of Mathematics
Like for Cosine and Sine, we need to pick the best formula to suit our question.
For example, if we need to find an unknown Opposite, then we should use the second “OPP = ” formula.
But if we are asked to find an unknown Angle Value, we should use the last formula which contains “Tan-1”.
Using the Calulator for Tan Values
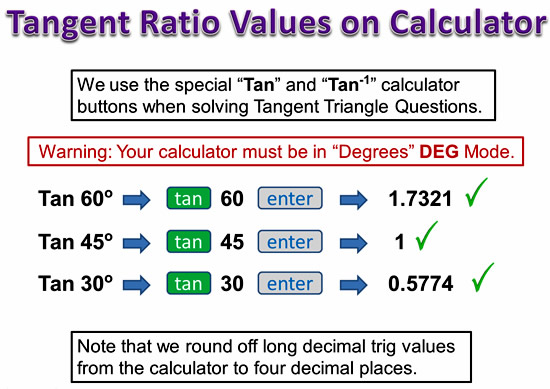
Image Copyright 2013 by Passy’s World of Mathematics
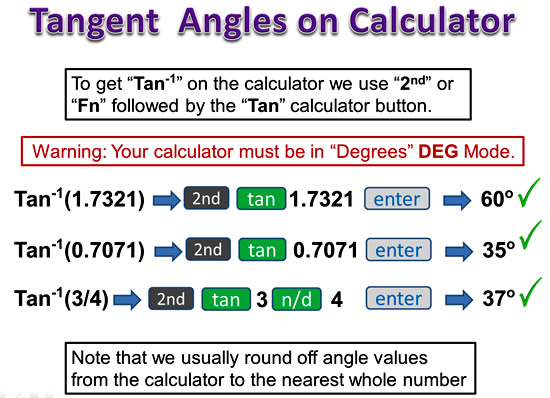
Image Copyright 2013 by Passy’s World of Mathematics
Steps for Tangent Questions
Follow these steps when doing any question which involves Opposite and Adjacent.

Image Copyright 2013 by Passy’s World of Mathematics
Tangent Examples
The following two examples show how to do a side length and Angle calculation for a Tangent type triangle.
Note that we would use SOH-CAH-TOA to work out that these triangle have Opposite and Adjacent larked on them, which means we have “OA” which fits into the “TOA” tan part of our method.
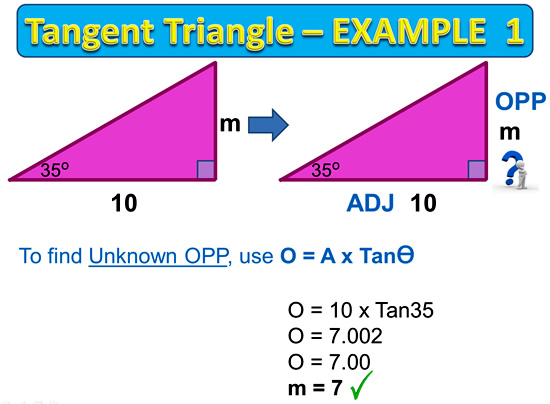
Image Copyright 2013 by Passy’s World of Mathematics
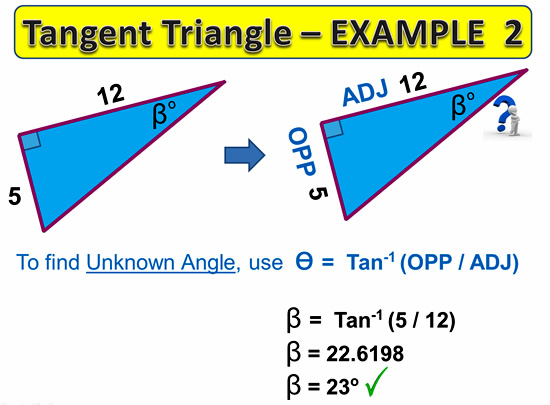
Image Copyright 2013 by Passy’s World of Mathematics
Practical Application of Tan Ratio

Image Source: http://www.mirror.co.uk
At the start of this lesson, we looked at the Tan Ratio when a jet airliner takes off.
Sometimes planes also have to make emergency landings, or even crash landings.
When a plane comes down in an emergency situation, there is the force of it hitting the ground coming straight upwards at passengers.
There is also a sudden horizontal force as the plane dramatically slows down as it makes contact with the ground, which throws passengers forward, like when a car slams on its brakes.
This results in a Tan situation, where the combined forces will resolve into an effective downhill force along the hypotenuse of a right triangle.
In their episode on “The Brace Position” for airline crashes, The Mythbusters use a Triangle Rig and make use of the Tan Ratio to simulate a plane crash landing.
The following short video gives a great summary of this 30 minute episode.
The full 30 minute episode is available on Discovery Channel DVD, and is well worth watching during a Math class on Triginometry.
Tangent Ratio Worksheets
Do any of the following worksheets for practice with Tangent Ratio Questions
Trigonometry Summary Sheet
Image Copyright 2013 by Passy’s World of Mathematics
If you would like a free A4 Summary Sheet of the Sin Cos and Tan formulas that we use in Trig Ratios, then click the link below.
SOH-CAH-TOA Pyramids

Image Copyright 2013 by Passy’s World of Mathematics
We can use a set of three pyramids to get all of our Trig Ratio Formulas.
Some people might find it easier to set up the following SOH-CAH-TOA Formula Pyramids, and use these to obtain formulas.
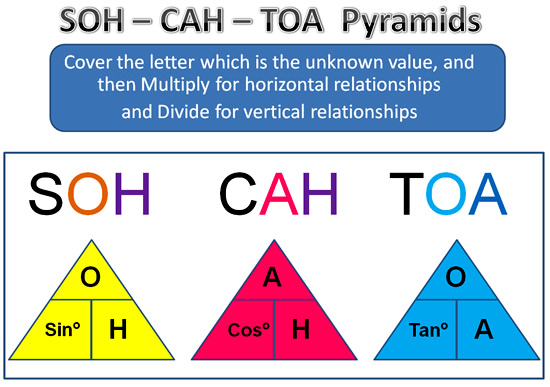
Image Copyright 2013 by Passy’s World of Mathematics
The Pyramids certainly provide a far more compact version of the full set of Trig Ratios Formulas.
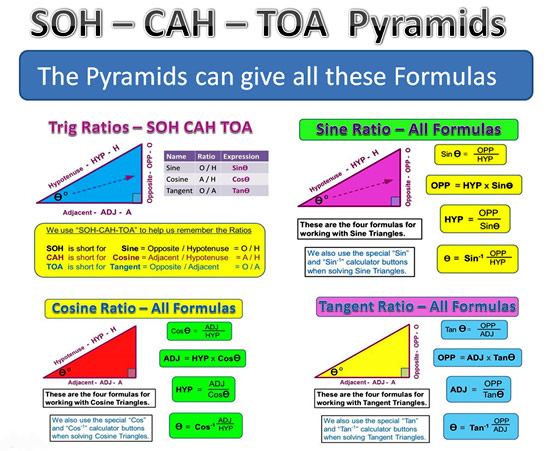
Image Copyright 2013 by Passy’s World of Mathematics
The Pyramids can be made in three simple steps:

Image Copyright 2013 by Passy’s World of Mathematics
In the second step we divide each pyramid in three, by ruling a horizontal line to form a smaller similar Triangle at the top
We then divide the bottom half Trapezoidal shape inh half.
In the Third step we write SOH CAH TOA into our pyramids, working from left to right.
The following diagram shows how things should look after completing steps 2 and 3.
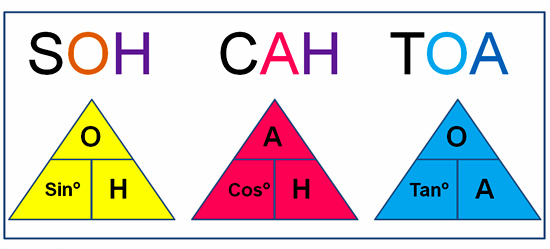
Image Copyright 2013 by Passy’s World of Mathematics
As much as we love Egypt and the Pyramids, we did NOT invent these SOH-CAH-TOA Pyramids here at Passy World.
We saw a maths teacher using them recently, and we also found pictures and explanations of them on the Internet.
Related Items
The Cosine Ratio
The Sine Ratio
Labeling Trigonometry Triangles
Trigonometric Ratios – Sin Cos and Tan
Classifying Triangles
Pythagoras and Right Triangles
Congruent Triangles
Tall Buildings and Large Dams
Similar Shapes and Similar Triangles
Geometry in the Animal Kingdom
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “The Tangent Ratio” Powerpoint.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Like Us on Facebook
Our Facebook page has many additional items which are not posted to this website.
These include items of mathematical interest, funny math pictures and cartoons, as well as occassional glimpses into the personal life of “Passy”.
Check it out at the following link:
https://www.facebook.com/PassysWorldOfMathematics
While you are there, LIKE the page so you can receive our FB updates to your Facebook News Feed.
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy