
Image Source: http://www.fanpop.com
Pythagoras Theorem and Trigonometry were key mathematical methods that were used to help build the Pyramids.
Pythagoras looked at the Sides Relationship, and people like Hipparcus looked at the Relationship between Angles and Sides.
They named the Angles and Sides mathematics “Trigonometry”.

Image Copyright 2013 by Passy’s World of Mathematics
In this lesson we look at the “Trigonometric Ratios” associated with Right Angled Triangles.
This lesson assumes that people already know how to label the Trigonometry sides of a Right Triangle as Hopenuse, Opposite, and Adjacent.
If you do not know how to do this sides labeling, then go and do our previous lesson on this at the link below.
http://passyworldofmathematics.com/trigonometry-labeling-triangles/
Trigonometric Ratios Example
Hipparcus and other ancient mathematicians found that when we have Similar Right Triangles, (which all have the same base angle), we get their internal sides ratios being identical.
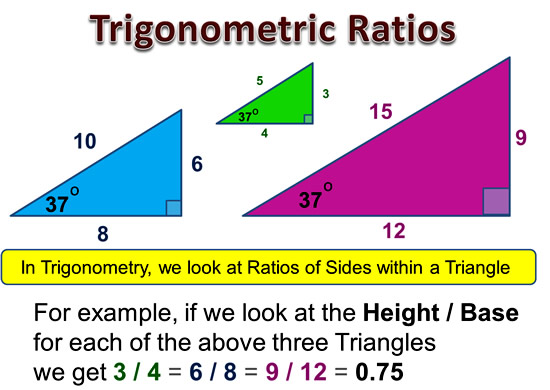
Image Copyright 2013 by Passy’s World of Mathematics
The above is only one example for a 37 degree base triangle; however it has been found that this concept works for any size base angle.
In addition, the above example only looks at the height versus the base of the triangles, but there are actually five other comparisons we can also do.
The full set of six Trigonometric Ratios is shown in the next section.
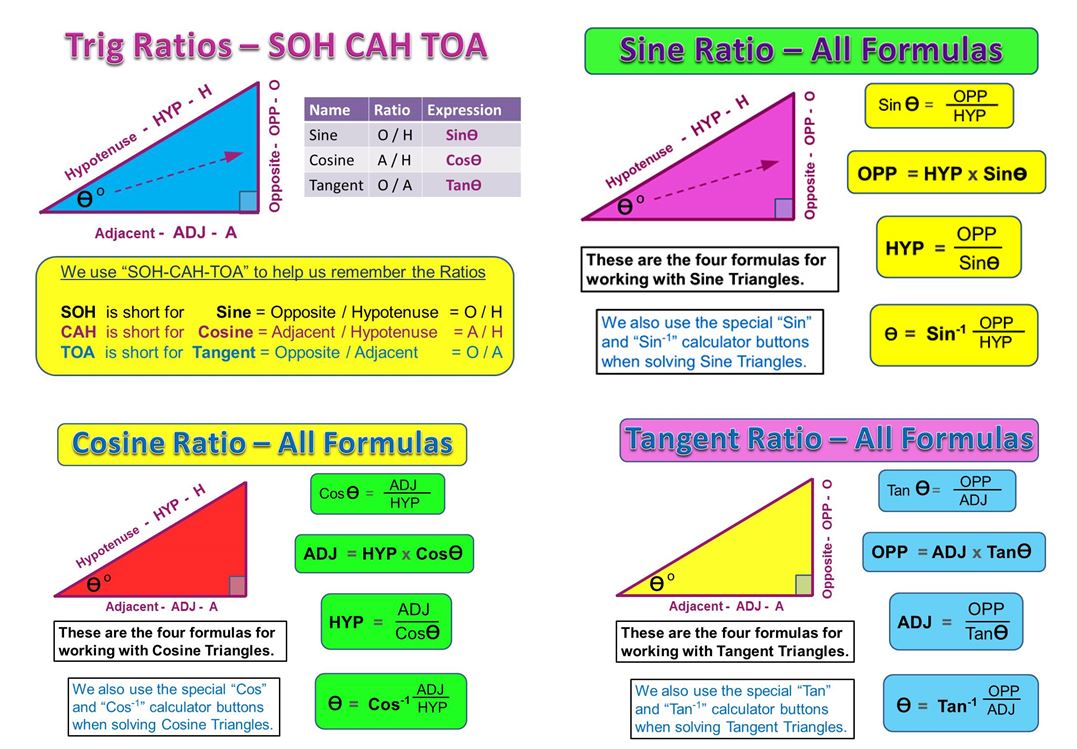
The Trigonometric Ratios
A Right Triangle has three sides: Hypotenuse, Opposite, and Adjacent.
If you do not know how to do this sides labeling, then go and do our previous lesson on this at the link below.
http://passyworldofmathematics.com/trigonometry-labeling-triangles/

Image Copyright 2013 by Passy’s World of Mathematics
The six Trigonometric ratios that we can make for a Right Triangle have special mathematical names as shown in the following Table.

Image Copyright 2013 by Passy’s World of Mathematics
We also have six math expressions which abbreviate these six names, and express the Trig Ratios in shorthand form.

Image Copyright 2013 by Passy’s World of Mathematics
In the remainder of this lesson, we will only be looking at three of these six ratios: Sine, Cosine, and Tangent.
SOH – CAH – TOA
To help memorize the three Trig Ratios for Sine, Cosine, and Tangent, the Acronym “SOH – CAH – TOA” is used.

Image Copyright 2013 by Passy’s World of Mathematics
Trigonometric Ratios Videos
Here is a short two and a half minute video which shows the Sine, Cosine, and Tangent Ratios.
This next seventeen minute video goes through the Trig Ratios, and does working out several example triangles.
Trig Ratio Examples
In this first example, we are given a Right Triangle with the sides labelled, and some number values for these sides.
We than use SOH-CAH-TOA to write the fraction and decimal values for Sin, Cos, and Tan for the 37 degree angle that is in the Right Triangle.

Image Copyright 2013 by Passy’s World of Mathematics
In this next example, the sides are not labeled and we are asked to find the Tan value of the unknow angle theta.
Using SOH-CAH-TOA, the Tan value is obtained by putting the Opposite side value over the Adjacent side value.

Image Copyright 2013 by Passy’s World of Mathematics
Our next example has the Cos value given to us, and we have to use it to work out the unknown Adjacent side on the Triangle.

Image Copyright 2013 by Passy’s World of Mathematics
This next example is similar to the previous example, but we are using the given Sine value to work out the Unknown “Opposite Side”.

Image Copyright 2013 by Passy’s World of Mathematics
This final example has a Cos value supplied, but it is for the top angle in the Triangle.
We need to label the Triangle, and then use Cos = Adjacent / Hypotenuse to work out the unknown Adjacent side “a”.

Image Copyright 2013 by Passy’s World of Mathematics
SOH-CAH-TOA Pyramids

Image Copyright 2013 by Passy’s World of Mathematics
We can use a set of three pyramids to get all of our Trig Ratio Formulas.
Some people might find it useful to set up the following SOH-CAH-TOA Formula Pyramids, and use these to obtain formulas.
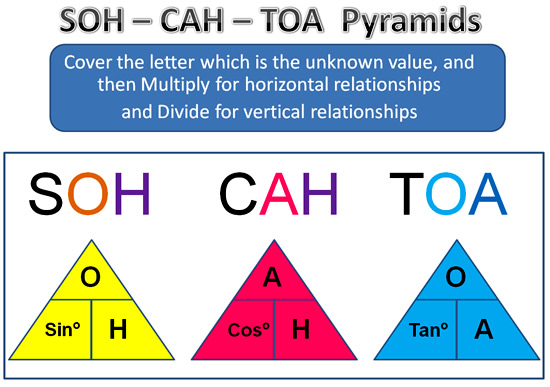
Image Copyright 2013 by Passy’s World of Mathematics
The Pyramids certainly provide a far more compact version of the full set of Trig Ratios Formulas.
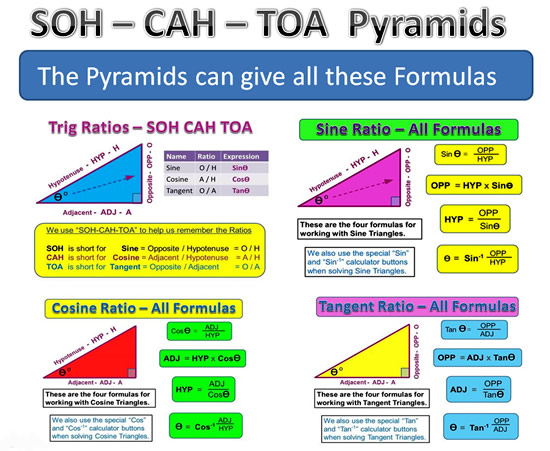
Image Copyright 2013 by Passy’s World of Mathematics
The Pyramids can be made in three simple steps:

Image Copyright 2013 by Passy’s World of Mathematics
In the second step we divide each pyramid in three, by ruling a horzontal line to form a smaller similar Triangle at the top
We then divide the bottom half Trapezoidal shape inh half.
In the Third step we write SOH CAH TOA into our pyramids, working from left to right.
The following diagram shows how things should look after completing steps 2 and 3.
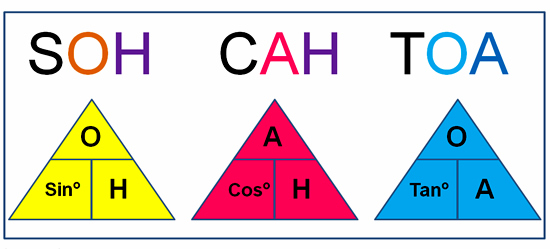
Image Copyright 2013 by Passy’s World of Mathematics
As much as we love Egypt and the Pyramids, we did NOT invent these SOH-CAH-TOA Pyramids here at Passy World.
We saw a maths teacher using them recently, and we also found pictures and explanations of them on the Internet.
Trigonometry Summary Sheet
Image Copyright 2013 by Passy’s World of Mathematics
If you would like a free A4 Summary Sheet which provides all of the Sin Cos and Tan formulas that we use in Trig Ratios, then click the link below.
SOH CAH TOA Music Video
Related Items
Labeling Trigonometry Triangles
The Sine Ratio
The Cosine Ratio
The Tangent Ratio
Classifying Triangles
Pythagoras and Right Triangles
Congruent Triangles
Tall Buildings and Large Dams
Similar Shapes and Similar Triangles
Geometry in the Animal Kingdom
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Trigonometry Ratios” Powerpoint.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Like Us on Facebook
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy





Pingback: Trigonometry – Labeling Triangles | Passy's World of Mathematics
Pingback: The Sine Ratio | Passy's World of Mathematics
Pingback: The Cosine Ratio | Passy's World of Mathematics
Pingback: The Tangent Ratio | Passy's World of Mathematics