
Image Source: PLane Landing at Maho Beach
Pilots need to use Trigonometry to make it onto the end of the runway when landing; particularly at Maho Beach in the Caribbean.
As the plane descends it has a speed at an angle, as well as a decreasing height, and its flight path forms the hypotenuse of a right triangle.
The pilot needs to use the correct angle and speed to make it onto the runway.
They also need to land at a point down the runway which still gives them enough length to stop the plane safely.

Image Copyright 2013 by Passy’s World of Mathematics
Here is a video showing just how difficult the landing at Maho Beach on San Maarten Island actually is.
Not only is it difficult to bring the plane down onto the runway, but in strong cross-winds the task is even made more difficult.
The pilot has to point the plane into the wind, so that it is not blown sideways off the runway.
The white bars that look like a Pedestrian Crossing at the end of the runway are used by incoming pilots for steering towards the runway at an angle to counteract the cross wind strength. This is very mathematical and the Pilot needs to get the exact answer!
There are some great examples of this in the following video.
Obviously the Pilot is far too busy during landings to do Trigonometry Calculations; however these calculations, along with many others, would be programmed into the computerised equipment that is giving status and warning indicators which are helping the pilot to successfully land the plane.
Trigonometry is also used in Navigation during the plane flight, in the form of “Bearings”, eg. fly for 200km at a bearing of North 20 degrees East.
Bearings are also used by ships and yachts setting their courses at sea.
Navigation and Bearings will be covered in a separate lesson, later in Trigonometry.
The Sine Ratio
There are three main Trigonometry Ratios: Sine, Cosine, and Tangent.
It is difficult to try and learn all three of these at once, and so this lesson only covers the Sine Ratio.
At Passy’s World, we have found that trying to learn all three Ratios at once, is like trying to learn how to Drive, Chip, and Putt, all in one Golf Lesson.
It is difficult, confusing, and frustrating.
We prefer to learn the Sine Ratio, and then the Cosine Ratio separately, before trying to deal with all three Trig Ratios.
Before doing this lesson on Sine Ratios, it is important that you know how to label the sides of a Right Triangle as “Hypotenuse”, “Opposite”, and “Adjacent”.
If you need to learn how to label a Right Triangle, then click the link below:
http://passyworldofmathematics.com/trigonometry-labeling-triangles/
The Sine Ratio involves the Opposite and Hypotenuse sides of a Right Triangle as follows:
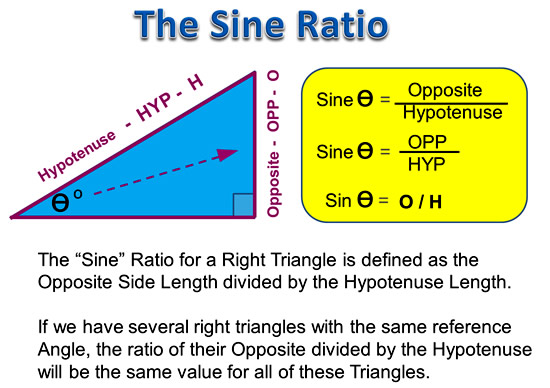
Image Copyright 2013 by Passy’s World of Mathematics
The Sine Ratio will be the same for any Right Triangle which has a particular Angle value contained in it.
The diagram below show this for three different sized 37 degree Right Triangles.
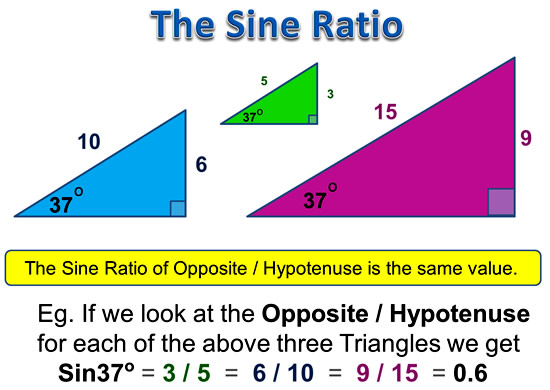
Image Copyright 2013 by Passy’s World of Mathematics
Opposite Side Formula
If we need to find the value of an Opposite Side for a Sine Triangle, and we have values for the reference angle and the hypotenuse, then we can derive and use the following formula.
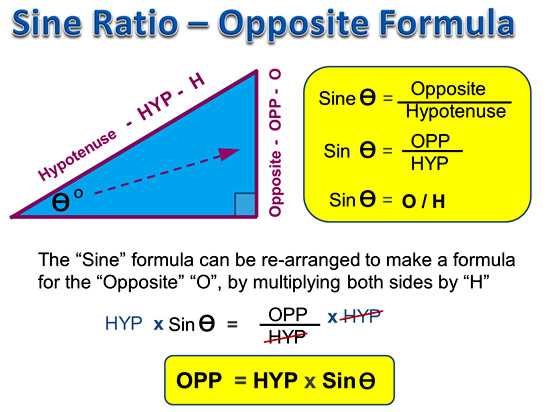
Image Copyright 2013 by Passy’s World of Mathematics
We use the above formula for finding unknown Opposite sides on Sine Triangles.
Note that we need to use a calculator when working with this formula; this is covered later in this lesson.
Hypotenuse Formula
If we take our previous Sine Triangle formula for the opposite, and do some rearranging, we can obtain a hypotenuse formula.
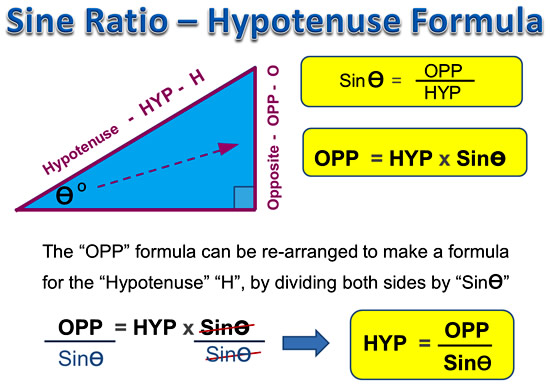
Image Copyright 2013 by Passy’s World of Mathematics
We use the above formula for finding unknown Hypotenuse values on Sine Triangles.
Note that we need to use a calculator when working with this formula; this is covered later in this lesson.
Angle Formula
The final Sine Triangle formula is for finding and unknown Angle, when we are given values for the opposite and the hypotenuse.
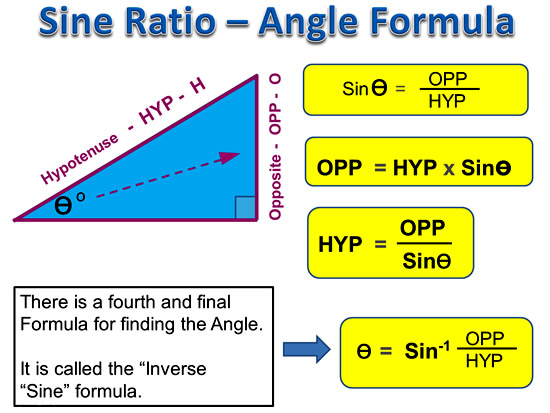
Image Copyright 2013 by Passy’s World of Mathematics
We use the above formula for finding unknown Angles on Sine Triangles.
Note that we need to use a calculator when working with this formula; this is covered later in this lesson.
Sine Triangle – Formulas Summary
Here are the four formulas we use when working with Sine Triangles.
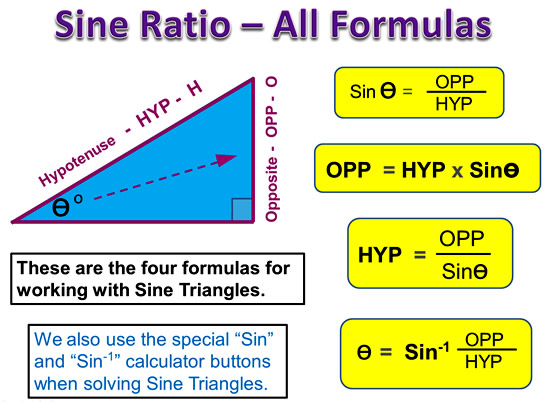
Image Copyright 2013 by Passy’s World of Mathematics
Using the Calculator for Sine Triangles
If we are given an angle and we need to determine its decimal Sine value, we can do this on a Calculator as shown below:
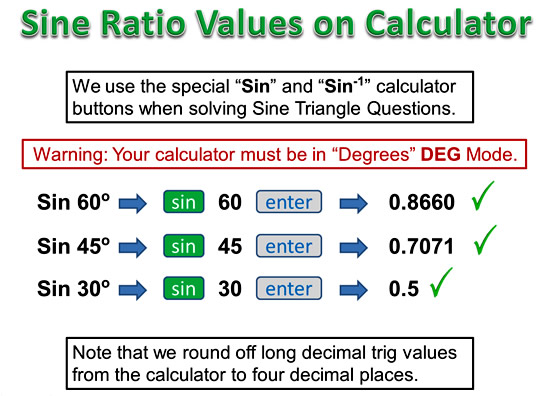
Image Copyright 2013 by Passy’s World of Mathematics
If we are given an Opposite and a Hypotenuse, and we need to determine the reference Angle value, we can do this on a Calculator as shown below:

Image Copyright 2013 by Passy’s World of Mathematics
The above function is sometimes also called finding the “ArcSin” or the “ASin”.
Online Trigonometry Calculator
If you would like to use an online calculator to find “Sin” or Angle values, then there is one at the following link:
Note that you will need to set this calculator to 4 decimal places for Sin values.
Sine Triangle – Working Out Steps
If we are working on a right triangle which involves an Opposite and a Hypotenuse, then here are the steps we need to follow.

Image Copyright 2013 by Passy’s World of Mathematics
Follow the above steps for doing all questions for Sine Triangles.
Sine Triangle Examples
The following examples show how we apply our Sine Triangle formulas to questions to work out unknown values on Right Triangles.
In this first example we are asked to find the value of the “opposite” side.
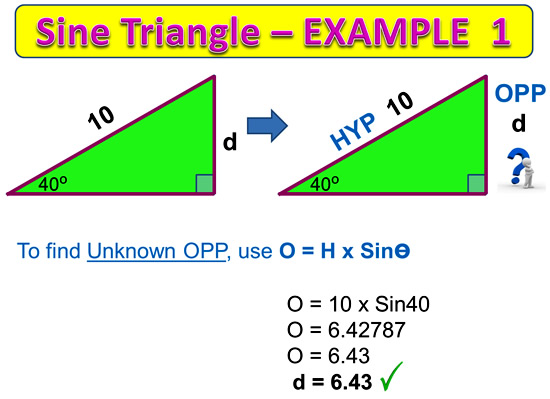
Image Copyright 2013 by Passy’s World of Mathematics
The next example shows how to find the value of the “Hypotenuse” for a Sine Triangle.
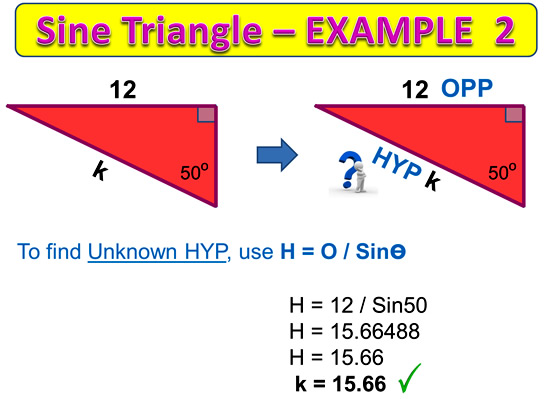
Image Copyright 2013 by Passy’s World of Mathematics
In our next example we use the Inverse Sine function to find an unknown Angle.
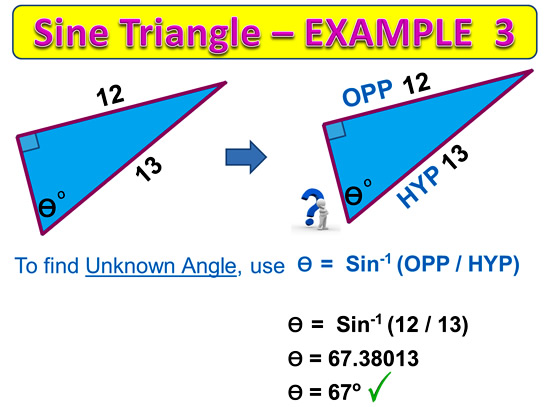
Image Copyright 2013 by Passy’s World of Mathematics
In this final example, we are given the Opposite and Hypotenuse, and asked to fine the decimal value of Sine.
It is important to read questions carefully, and not immediately assume that this is a Find the Angle example, like Example 3.
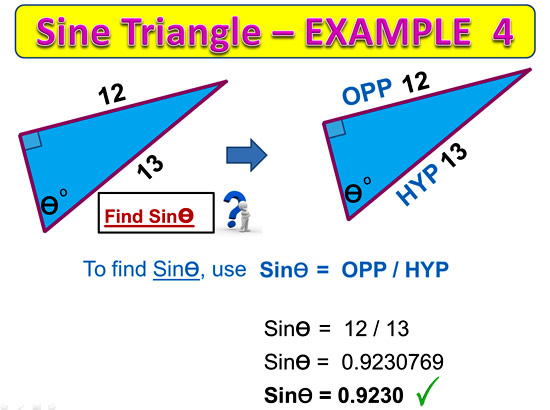
Image Copyright 2013 by Passy’s World of Mathematics
Application Question Example
The following three minute video shows how to do a real world application question that involves using the Sine Ratio.
Sine Ratio Worksheet
The following worksheet contains several type of Sine Ratio questions, and includes Answers at the end of the sheet.
Click the following link to access this Sine Ratio worksheet:
Related Items
Trigonometric Ratios – Sin Cos and Tan
Labeling Trigonometry Triangles
Classifying Triangles
Pythagoras and Right Triangles
Congruent Triangles
Tall Buildings and Large Dams
Similar Shapes and Similar Triangles
Geometry in the Animal Kingdom
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “The Sine Ratio” Powerpoint.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Like Us on Facebook
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy






Pingback: The Cosine Ratio | Passy's World of Mathematics
Pingback: The Tangent Ratio | Passy's World of Mathematics
Pingback: Trigonometric Ratios | Passy's World of Mathematics