
Image Source: http://resources3.news.com.au
Identical Twins have the exact same size and shape, and we instantly recognise that the two of them are exactly the same.
When two items have the exact same size and shape, we say that they are “Congruent”.
This lesson is all about “Congruent Triangles”, eg. pairs of Triangles which have the exact same size and shape.
Congruent Triangles are an important part of our everyday world, especially for reinforcing many structures.

Image Copyright 2013 by Passy’s World of Mathematics
Here are a typical pair of Congruent Triangles
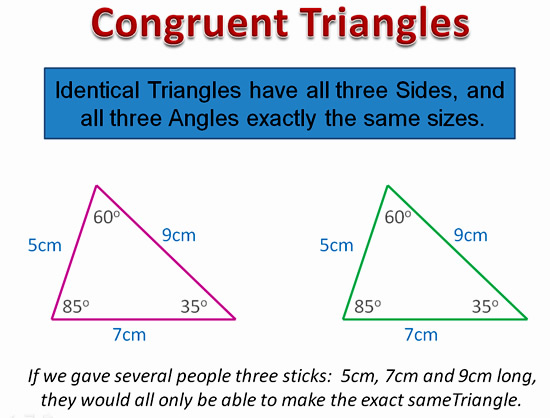
Image Copyright 2013 by Passy’s World of Mathematics
Two triangles are congruent if they are completely identical.
This means that the matching sides must be the same length and the matching angles must be the same size.
The Identical (eg.”Congruent”) Triangles can be in different positions, (or orientations), and still be the exact same size and shape.
The position of the matching Triangles does not affect the fact that they are identical, or “Congruent”.
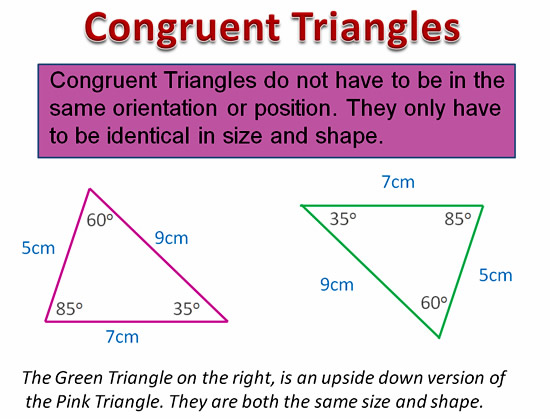
Image Copyright 2013 by Passy’s World of Mathematics
Introductory Video About Congruency
The following Video by Mr Bill Konst about Congruence, covers the “SSS Rule for Triangles”, as well as covering Quadrilaterals and some interesting optical illusions.
Shortcut Rules for Congruent Triangles
It turns out that we do not have to check all the sides and angles of two Triangles to work out that they are Congruent.

Image Copyright 2013 by Passy’s World of Mathematics
There are FOUR “Shortcut Rules” for Congruent Triangles that we will be covering in this lesson.
The first of these “Shortcut Rules” is the “Side Side Side”, or “SSS” Rule.
SSS – Side Side Side Rule for Triangles
We can actually use just the three sides to work out if two triangles are congruent.
This is called “SSS” or the “Side Side Side Rule”.
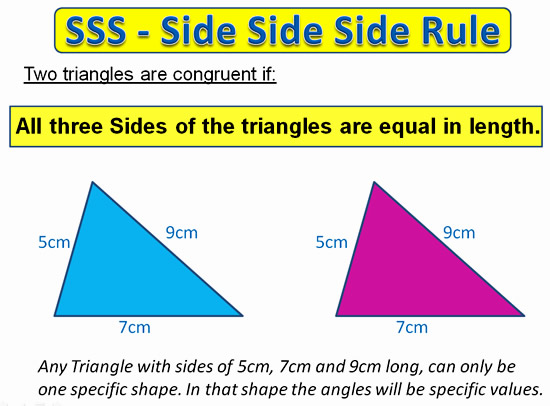
Image Copyright 2013 by Passy’s World of Mathematics
In diagrams, the actual values of the sides are sometimes not given.
Instead we have markers to show where the matching same length sides are on the two triangles.
For these Triangles we can apply the “SSS” rule, as long as we have all three sides matching each other on the two triangles.
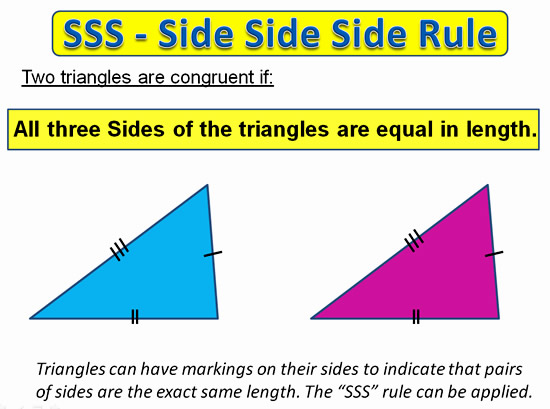
Image Copyright 2013 by Passy’s World of Mathematics
Symbols Used in Congruency
There is a special symbol we use to indicate that Triangles are Congruent, that is like an equals sign with an extra line added on top of it.
This triple ine symbol is what we use in Australia; however some other countries use an equals sign with a squiggly “tilda” line added to the top of it.
In addition, Triangles are usually labelled with capital alphabet letters.
When we say the Triangles are Congruent using their letters, we need to make sure the order of the letters matches the path around the two triangles correctly.
This is shown in the following example.

Image Copyright 2013 by Passy’s World of Mathematics
We need to be careful with the labelling when our Triangles are in different positions.
Eg. We need to make sure the order of the letters matches going around the two triangles in the same order of sides. Going A to B to C should be the exact same path as D to E to F.
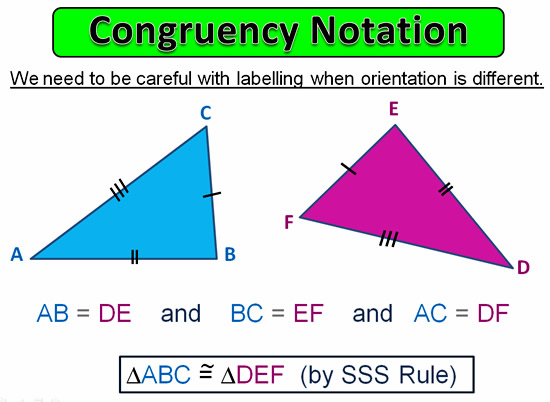
Image Copyright 2013 by Passy’s World of Mathematics
SAS – Side Angle Side Rule for Triangles
Two Triangles will be congruent if two matching sides have equal lengths and
the angle included by these sides is the same.
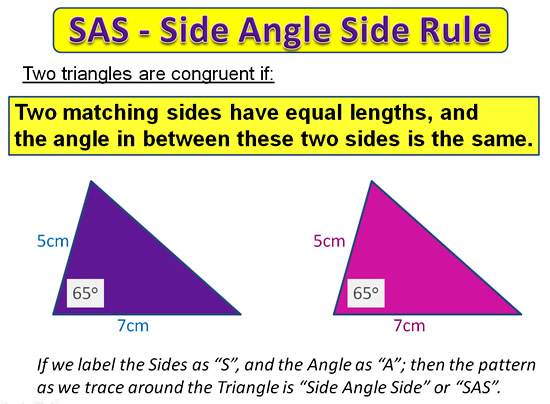
Image Copyright 2013 by Passy’s World of Mathematics
The following video covers the “SSS” and “SAS” Rules for Congruent Triangles.
The American teacher doing the videos does not always use the most correct language, but he is enthusiastic and explains his examples well.
AAS – Angle Angle Side Rule for Triangles
Two triangles are congruent if two matching angles are equal and a matching side is equal in length.
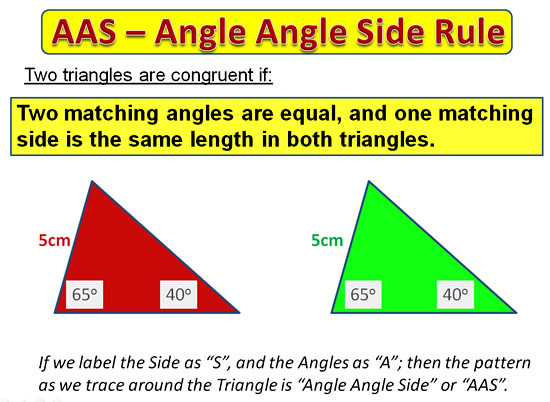
Image Copyright 2013 by Passy’s World of Mathematics
There is also an old “ASA” Angle Side Angle Rule; however this has been brought in to be part of the “AAS” Rule.

Image Copyright 2013 by Passy’s World of Mathematics
It is quite okay to use the “ASA” Rule if the order of the items is “ASA” as shown in the above diagram.
However, most people these days just use “AAS”, so that there is one less congruency rule to memorise.
The following “YayMath” 26 minute gives a comprehensive lesson on the ASA and AAS Rules.
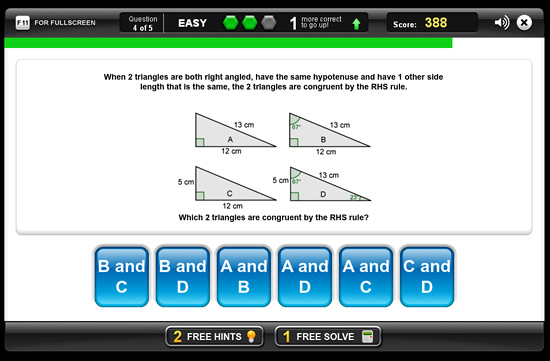
RHS – Right Angle Hypotenuse Rule
Any two Right-Angled 90 degree Triangles are congruent if the hypotenuse and one pair of matching sides are equal in length.
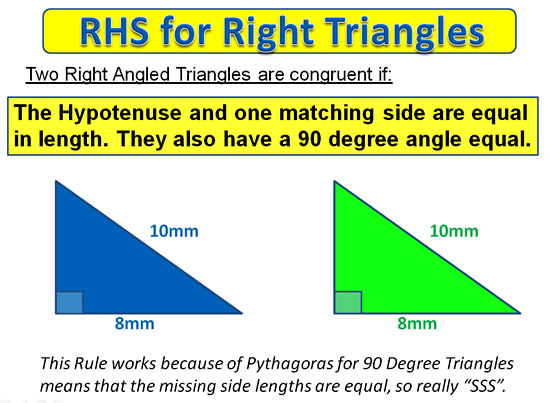
Image Copyright 2013 by Passy’s World of Mathematics
This Rule works because of Pythagoras Theorem for 90 Degree Triangles.
Pythagoras Rule means that the missing side lengths have to be equal, so we are indirectly using the “SSS” Rule here.
Why the SSA Rule Does Not Exist
The following video shows why there is not an SSA Rule for congruent triangles.
Triangle Rules Summary
There are four rules that we use to determine if Triangles are congruent: SSS, SAS, AAS, and RHS.
These are shown in the diagram below:
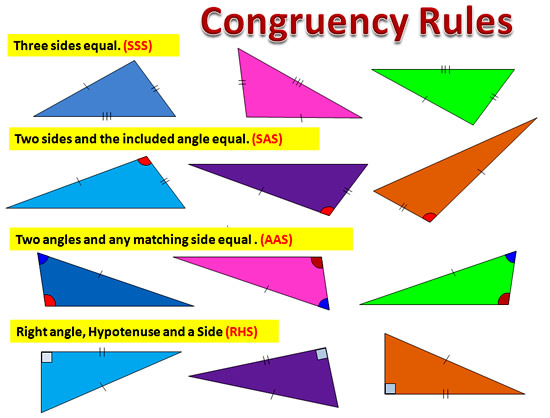
Image Copyright 2013 by Passy’s World of Mathematics
Congruent Triangles Music Videos
Here is a quick little tune by Abbie about the Triangle Rules, mentioning exclusion of the invalid Angle Side Side “Donkey Rule”.
This next one is a heavy metal Parody (sounds a bit like a Joan Jet song):
Congruent Triangles Examples
The following examples show the required working out for demonstrating that a pair of Triangles are identical.
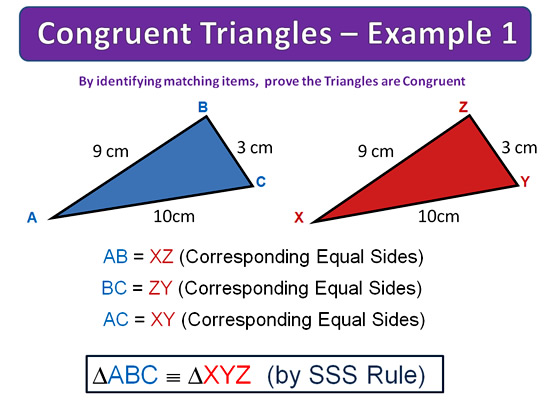
Image Copyright 2013 by Passy’s World of Mathematics
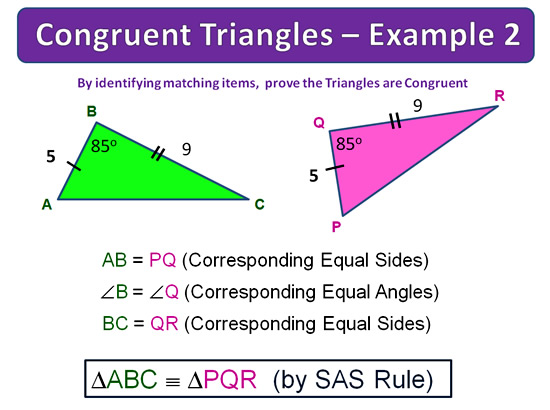
Image Copyright 2013 by Passy’s World of Mathematics
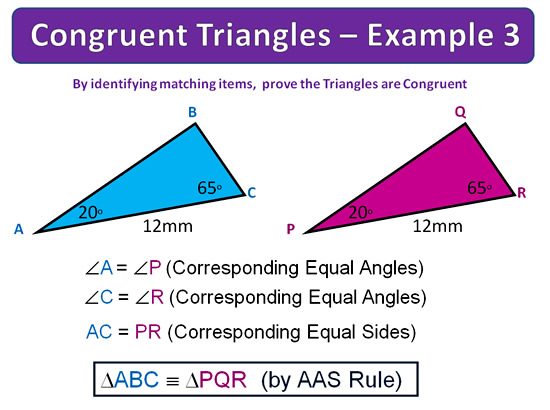
Image Copyright 2013 by Passy’s World of Mathematics
Composite Shapes Examples
The following video shows some more complex examples, where triangle sides are joined together to other triangles and shapes.
In the next two examples, Congruent Triangles are found within the given Geometric Shapes, which allows side lengths to be proven as equal.
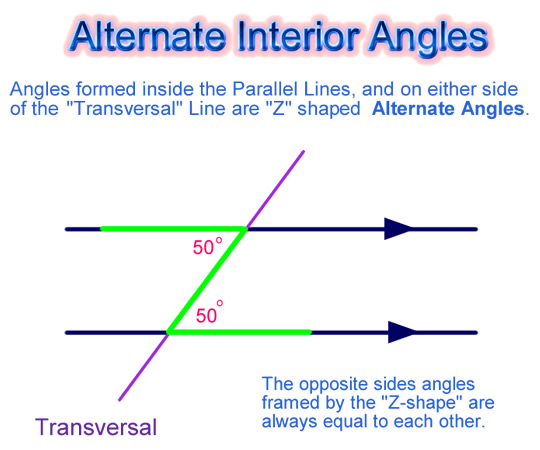
Rules for Angles in Parallel Lines are also used, in particular, the following Alternate Interior Angles Rule:
This first example is the classic “Bow Tie” shaped question for joined congruent triangles.
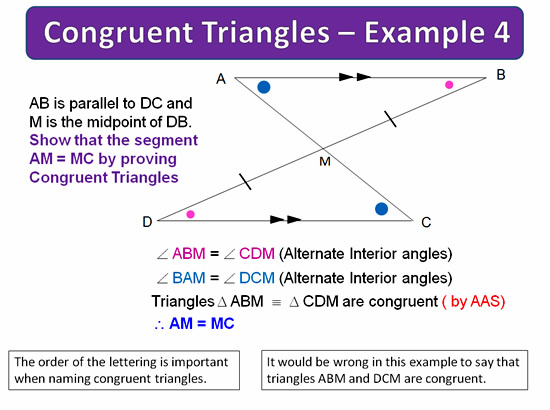
Image Copyright 2013 by Passy’s World of Mathematics
The next example involves two triangles sharing the diagonal of a Parallelogram.
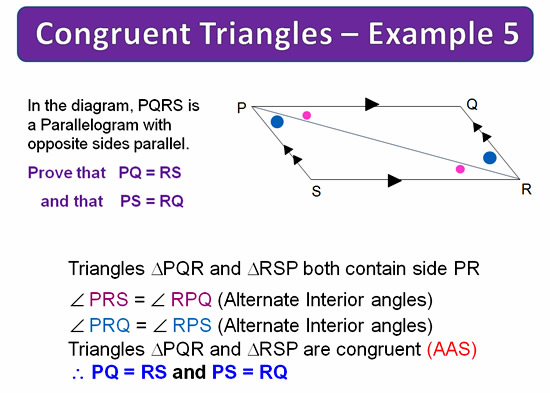
Image Copyright 2013 by Passy’s World of Mathematics
Congruent Triangles Worksheets
The following worksheet has basic multiple choice questions on Congruent Triangles.
(There are answers on the last page of the PDF document).
The following video has an worked example to get you started.
Click the link below to do this worksheet:
The following worksheet has medium level of difficulty multiple choice questions on Congruent Triangles.
(There are answers on the last page of the PDF document).
The following video has an worked example to get you started.
Click the link below to do this worksheet:
This last worksheet has challeging multiple choice questions on Congruent Triangles.
(There are answers on the last page of the PDF document).
The following video has an worked example to get you started.
Click the link below to do this worksheet:
Congruent Triangles Games
The above game is a matching game with several levels of difficulty.
It is more like a Quiz than a Game, but will help you learn congruent triangles.
Click the link below to play this game.
http://www.mangahigh.com/en_au/maths_games/shape/congruence/congruent_triangles
This next game involves dropping the shapes into the correct boxes using the arrow keys.
It also contains multiple choice questions that need to be answered.
Click the link below to play this game.
http://www.classzone.com/books/geometry_concepts/page_build2.cfm?CFID=15754374&ch=5&id=game
The following is an activity where we get to build congruent triangles based on the congruency rule we pick to work with.
Click the link below to play this game.
http://illuminations.nctm.org/ActivityDetail.aspx?ID=4
This final game is a Jeapordy Game, but is very slow to load up.
Click the link below to play this game.
http://www.superteachertools.com/jeopardyx/jeopardy-review-game.php?gamefile=1322685871
Related Items
Classifying Triangles
Angle Sum in a Triangle
Exterior Angle of a Triangle
Angles and Parallel Lines
Pythagoras and Right Triangles
Jobs that use Geometry
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Congruent Triangles” Powerpoint.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Like Us on Facebook
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy







Pingback: Similar Triangles | Passy's World of Mathematics
Pingback: Geometry in the Animal Kingdom | Passy's World of Mathematics
Pingback: Jobs With Geometry | Passy's World of Mathematics
Pingback: Trigonometry – Labeling Triangles | Passy's World of Mathematics
Pingback: The Sine Ratio | Passy's World of Mathematics
Pingback: The Cosine Ratio | Passy's World of Mathematics
Pingback: Trigonometric Ratios | Passy's World of Mathematics
Pingback: The Tangent Ratio | Passy's World of Mathematics