
Image Source: http://img.izismile.com
Venn Diagram Word Problems can be very easy to make mistakes on when you are a beginner.
It is extremely important to:
Read the question carefully and note down all key information.
Know the standard parts of a Venn Diagram
Work in a step by step manner
Check at the end that all the numbers add up coorectly.
Let’s start with an easy example of a two circle diagram problem.
Venn Diagrams – Word Problem One
“A class of 28 students were surveyed and asked if they ever had dogs or cats for pets at home.
8 students said they had only ever had a dog.
6 students said they had only ever had a cat.
10 students said they had a dog and a cat.
4 students said they had never had a dog or a cat.”
Note that the word “only” is extremely important in Venn Diagram word problems.
Because the word “only” is in our problem text, it makes it an easy word problem.
Since this question is about dogs and cats, it will require a two circle Venn Diagram.
Here is the type of diagram we will need.
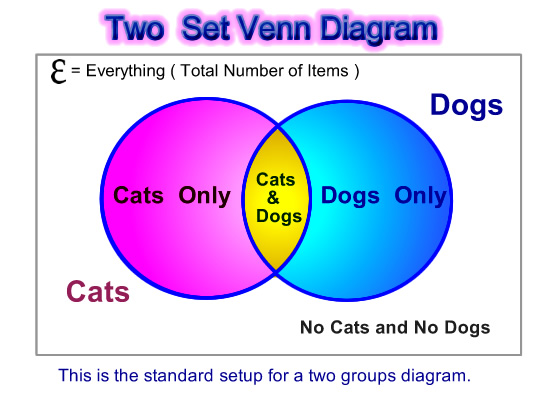
Image Source: Passy’s World of Mathematics – Copyright 2012
Our problem is an easy one where we have been given all of the numbers for the items required on the diagram.
We do not need to work out any missing values.
All we need to do is place the numbers from the word problem onto the standard Venn Diagram and we are done.
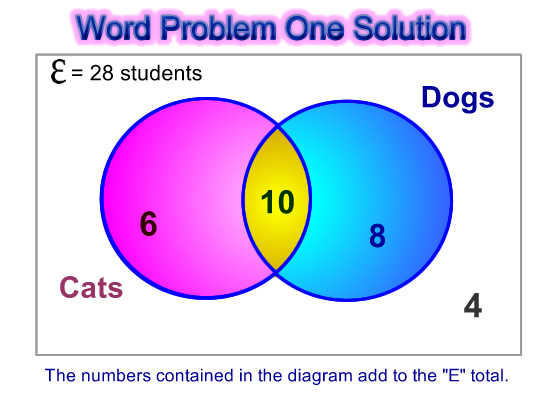
Image Source: Passy’s World of Mathematics – Copyright 2012
Venn Diagrams – Word Problem Two
The answer for this question will actually be the same as the Cats and Dogs question in Example 1.
However this time we are given less information, and so we will have work out the missing information.
Here is Problem 2:
“A class of 28 students were surveyed and asked if they ever had dogs or cats for pets at home.
18 students said they had a dog.
16 students said they had a cat.
4 students said they had never had a dog or a cat.”
Note that the word “only” is extremely important in Venn Diagram word problems.
The above question does not contain the word “only” anywhere in it, and this is an indication that we will have to do some working out.
The question states that: “18 students said they had a dog” without the word “only” in there.
This means that the total of the Dogs circle is 18.
The 18 total students for Dogs includes people that have both a cat and a dog, as well as people who only have a dog.
Some people, who do not read this question carefully, will simply take the above figures and put them straight into a Venn Diagram like this.
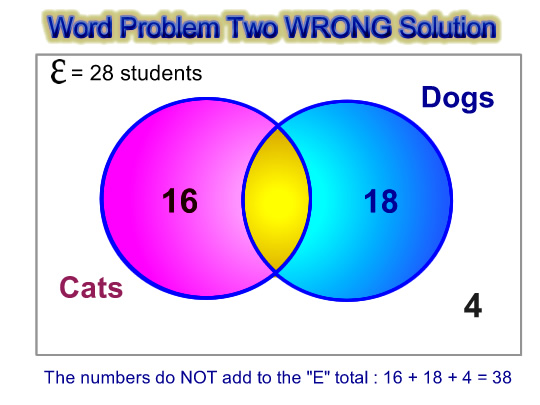
Image Source: Passy’s World of Mathematics – Copyright 2012
Always check at the end that the numbers add up to the “E” Grand total.
16 + 18 + 4 = 38 which is much bigger than the “E” total of 28.
This is because some students have both a cat and a dog. We have not accounted for this at all.
Other people might think that we do not have enough information, and it is therefore impossible to do this problem. This is simply not true.
Let’s put down on our diagram all of the information we have been given.
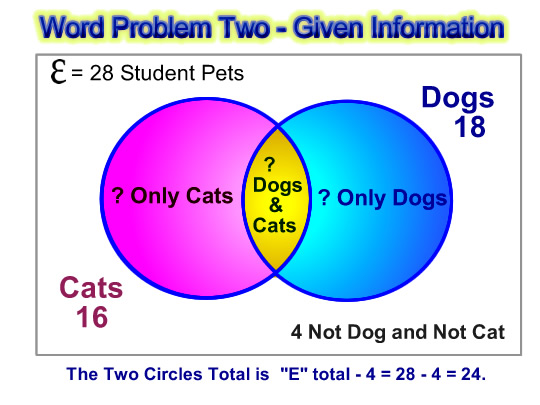
Image Source: Passy’s World of Mathematics – Copyright 2012
From the given information we have been able to work out that the circles total is 24. (Eg. Everything Total – No Cats and No Dogs = 28 – 4 = 24.
This is vital information we now use to work on the rest of the problem.
Let’s first work out the “Only Cats” value.
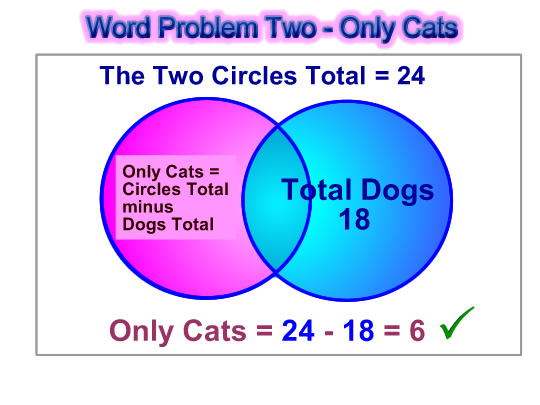
Image Source: Passy’s World of Mathematics – Copyright 2012
Next we work out the “Only Dogs” number of people.
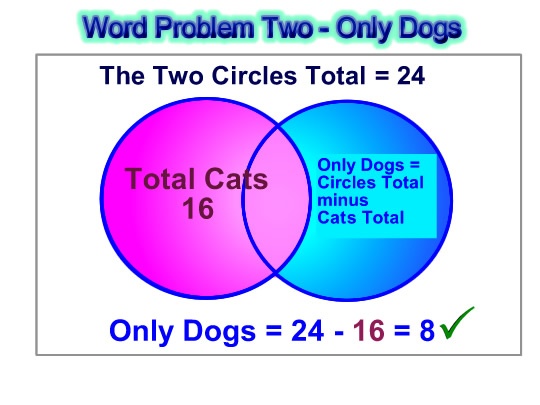
Image Source: Passy’s World of Mathematics – Copyright 2012
Let’s now fill in all of the information we have worked out so far.
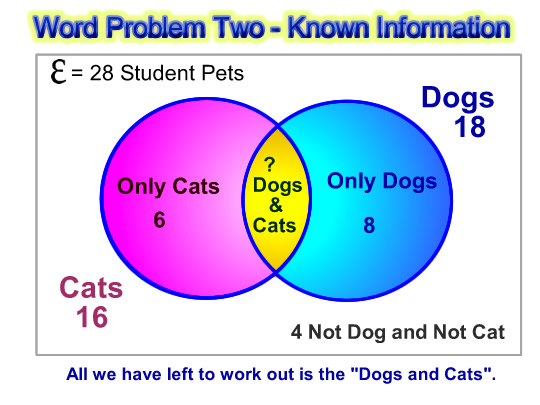
Image Source: Passy’s World of Mathematics – Copyright 2012
All we have left to work out is the number of Cats and Dogs for the center of the diagram.
We can do this any of three possible ways:
Cats and Dogs = Total Cats – Only Cats
or
Cats and Dogs = Total Dogs – Only Dogs
or
Cats and Dogs = E Total – Only Cats – Only Dogs – (No cats and No Dogs)
Any way that we work it out, the answer is 10.
So here is the final completed Venn Diagram Answer.

Image Source: Passy’s World of Mathematics – Copyright 2012
When putting answers into our Mathematics Workbook, we do not have to color in the diagram.
A final answer like the following is quite acceptable.
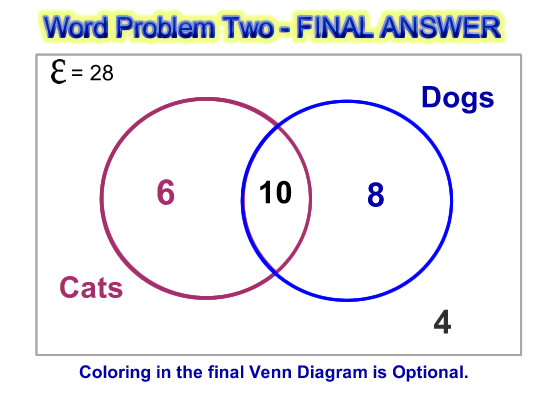
Image Source: Passy’s World of Mathematics – Copyright 2012
We can summarise the steps we used to work out this problem as follows.
Word Problem Two – Summary of Steps
– Work out What Information is given, and what needs to be calculated.
– Circles Total = E everything – (No Cats and No Dogs)
– Cats Only = Circles Total – Total Dogs
– Dogs Only = Circles Total – Total Cats
– Cats and Dogs = Cats Total – Cats Only
– Finally, check that all the numbers in the diagram add up to equal the “E” everything total.
Word Problem Three – Subsets
“Fifty people were surveyed and only 20 people said that they regularly eat Healthy Foods like Fruit and Vegetables.
Of these 20 healthy eaters, 12 said that they ate Vegetables every day.
Draw a Venn Diagram to represent these results.”
This problem is quite different to our other two circle diagrams.
Cats and Dogs are very different to each other, and so we needed two separate circles.
However Healthy Foods and Vegetables are not different to each other because Vegetables are a type of Healthy Food.
We say that vegetables are a “Subset” of Healthy Foods.
This means that we do not separate the circles. We actually need to draw our circles inside each other like this.

Image Source: Passy’s World of Mathematics – Copyright 2012
The total adds up to 50, and the 12 people who include vegetables in their healthy foods are shown as being fully inside the Healthy Foods circle.
Word Problem Four – Disjoint Sets
“Draw a Venn Diagram which divides the twelve months of the year into the following two groups:
Months whose name begins with the letter “J” and Months whose name ends in “ber”. You will need a two circle Venn Diagram for your answer.”
The first step is to list the twelve months of the year:
January – named after Janus, the god of doors and gates
February – named after Februalia, when sacrifices were made for sins
March – named after Mars, the god of war
April – from aperire, Latin for “to open” (buds)
May – named after Maia, the goddess of growth of plants
June – named after junius, Latin for the goddess Juno
July – named after Julius Caesar in 44 B.C.
August – named after Augustus Caesar in 8 B.C.
September – from septem, Latin for “seven”
October – from octo, Latin for “eight”
November – from novem, Latin for “nine”
December – from decem, Latin for “ten”
Months starting with J = { January, June, July }
Months ending in “ber” = { September, October, November, December }
The two sets do not have any items in common, and so we will not overlap them.
The remaining months will need to go outside of our two circles.
There should be all twelve months in the diagram when we are finished.
The completed Venn Diagram is shown below:

Image Source: Passy’s World of Mathematics – Copyright 2012
Venn Word Problems – Summary
We have not included three circle diagrams, as they will be covered in a separate lesson.
Remember that the setup for a two circle Venn Diagram is usually like this:
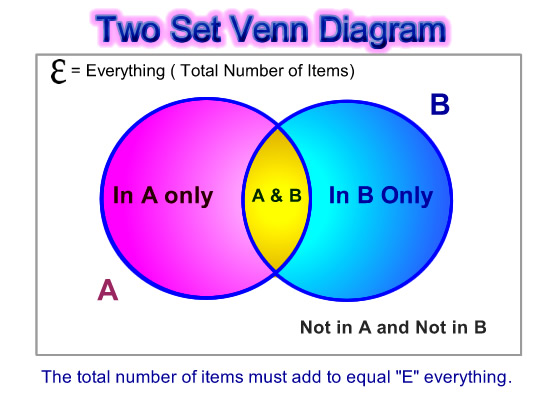
Image Source: Passy’s World of Mathematics – Copyright 2012
Remember the working out steps for harder problems are:
Work out What Information is given, and what needs to be calculated.
Check to see if the two sets are “Subsets” or “Disjoint” sets.
If they are “Intersecting Sets” then some of the following formulas may be needed.
Circles Total = E everything – (Not in A and Not in B)
In A Only = Both Circles Total – Total in B
In A Only = The A Circle Total – Total in the intersection (A and B)
In B Only = Both Circles Total – Total in A
In B Only = The B Circle Total – Total in the intersection (A and B)
In the Intersection (A and B) = Total in B – In B Only
In the Intersection (A and B) = Total in A – In A Only
Finally, check that the numbers in the diagram all add up to equal the “E” everything total.
Venn Word Problems Videos
The following video shows a typical two circles word problem.
Here is a video that covers a two circles problem, where we need to find the number of items that are ( not in “A” and not in “B”)
Here is a Video which shows how to solve Venn Diagram Survey Problems.
The following video is another very good one from “YourMathGal” about how to draw Venn Diagrams for word problems.
Related Items
Introduction to Venn Diagrams
Three Circle Venn Diagrams
Real World Venn Diagrams
If you enjoyed this post, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our blog, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Venn Diagrams Word Problems” Powerpoint.
Like Us on Facebook
Our Facebook page has many additional items which are not posted to this website.
These include items of mathematical interest, funny math pictures and cartoons, as well as occassional glimpses into the personal life of “Passy”.
Check it out at the following link:
https://www.facebook.com/PassysWorldOfMathematics
While you are there, LIKE the page so you can receive our FB updates to your Facebook News Feed.
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy





Pingback: Three Circle Venn Diagrams | Passy's World of Mathematics
Pingback: Venn Diagrams Introduction | Passy's World of Mathematics
Pingback: Real World Venn Diagrams | Passy's World of Mathematics