The above picture is called a “Venn Diagram”, or “Venn-Euler Diagram”.
It shows the similarities and differences between Moths and Butterflies.
The characteristics of moths have been placed in the green circle, and butterflies in the blue circle.
Because the two insects have some common features, the two circles have been made to overlap each other.
The common features are put into this common area, where the two circles cross each other and overlap.
This overlapping region is called the “Intersection” of the Venn Diagram.
The diagram is put inside a big rectangle which is called the “Universal Set”.
The “Universal Set” rectangle contains inside it everything that we have listed about Moths and Butterflies.
Definition of a Set
A “Set” is a collection of items that belong to a well defined category or group.
For example, a fish belongs to the group of animals which live in water.
Sets are enclosed in pairs of curly brackets { }
For example, we could write the following for the set of our favorite animals which live in water:
Water Animals = { Fish, Eel, Platypus }
“Elements” are the items in sets.
Eg. “Fish” is an element of { Water Animals } .
We can have another set of our favorite animals written like this:
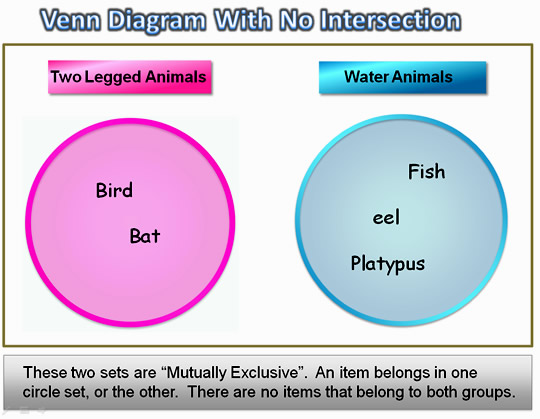
Two Legged Animals = { Birds, Bats }
When we draw the Venn Diagram for these two sets, there is nothing in common between the two groups.
We call these two sets “Mutually Exclusive”. This means any item must belong to only one of the sets, and the two sets have nothing in common.
Complementary Sets
The “complement” of a set is everything not in that set. (Symbol A’)
For our previous two circles inside the rectangle universal set, we have the two sets:
Water Animals = { Fish, Eel, Platypus }
Two Legged Animals = { Birds, Bats }
The complement of Water Animals is all of the animals in our Venn Diagram that are not inside the Water Animals circle.
Therefore the complement of the Water Animals is the set:
Water Animals’ = { Bird, Bat }
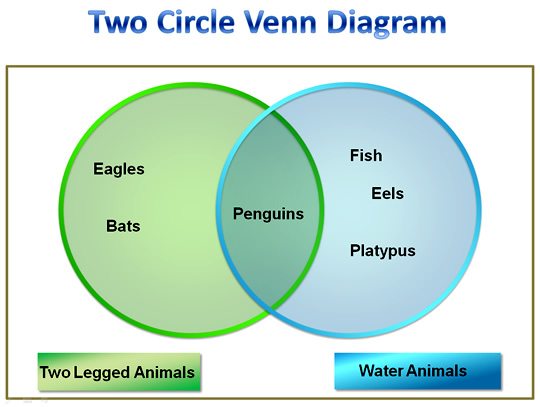
Two Circle Venn Diagram
Let’s change our previous example so that it now contains the following Universal set of Animals:
E = Everything = { Fish, Eels, Platypus, Penguins, Eagles, Bats }
We are going to use a Venn diagram to divide these animals into the following two sets:
“Water Animals” and “Two Legged Animals” .
When we do this, we find that Penguins belong in both groups:
E = Everything = { Fish, Eels, Platypus, Penguins, Eagles, Bats }
Water Animals = { Fish, Eels, Platypus, Penguins }
Two Legged Animals = { Eagles, Bats, Penguins }
This means that on our Venn Diagram, we will need to have two overlapping circles, so that we can put Penguins inside both circles.
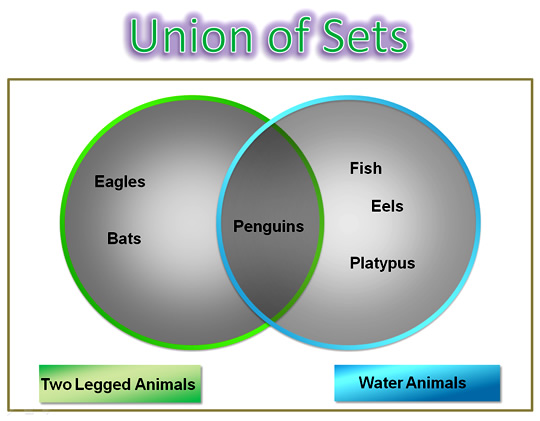
Union of Sets
The union of two sets is everything that is contained within the two circles joined together.
It is the combined total of the two sets, where each item is only listed once.
For our Venn Diagram of Two Legged Animals and Water Animals, we have:
{ Two Legged Animals } Union { Water Animals } =
{ Fish, Eels, Platypus, Penguins, Eagles, Bats }
Union is often written using a big “U” symbol, or the word “OR”.
Difference Between “OR” and “AND”
The word “OR” is used for Union.
“OR” actually means that everything in our Union answer set is either in one circle, OR in the other circle.
The word “AND” in sets is used for “Intersection” and means that the item is contained in both sets.

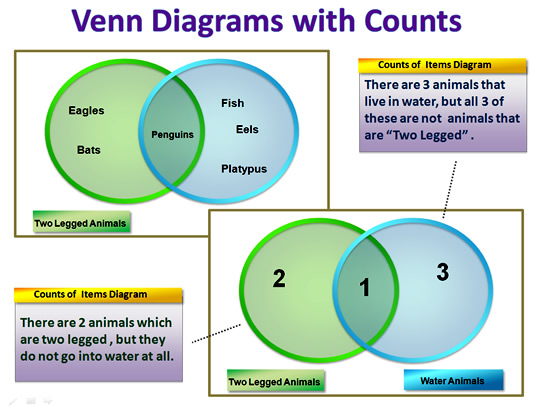
Venn Diagrams with Counts
Often Venn Diagrams do not list all the individual item names in the diagram.
Instead they list a count of how many items there are in each particular group.
This is shown in the diagram below, where we have converted our Animals Diagram into a Counts Diagram.
Venn Diagrams Summary
The main concepts covered in this introduction have been Union, Intersection, Mutually Exclusive, and Complements as applied to two circle Venn Diagrams.

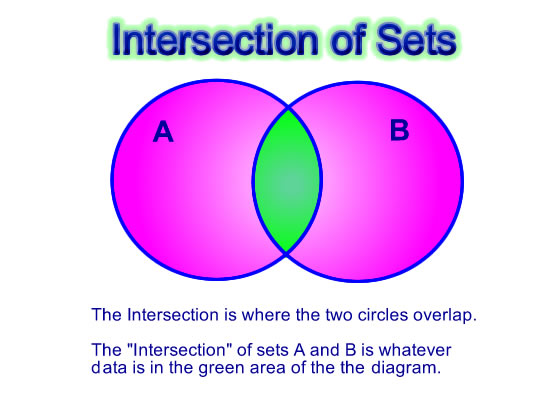
Image Source: Passy’s World of Mathematics
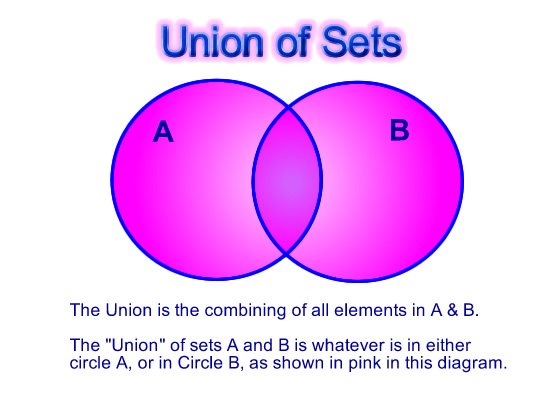
Image Source: Passy’s World of Mathematics
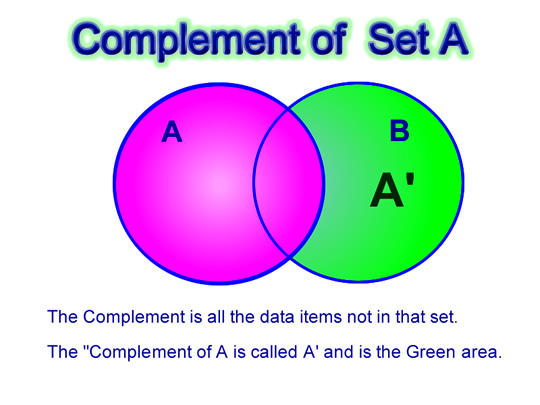
Image Source: Passy’s World of Mathematics

Image Source: Passy’s World of Mathematics
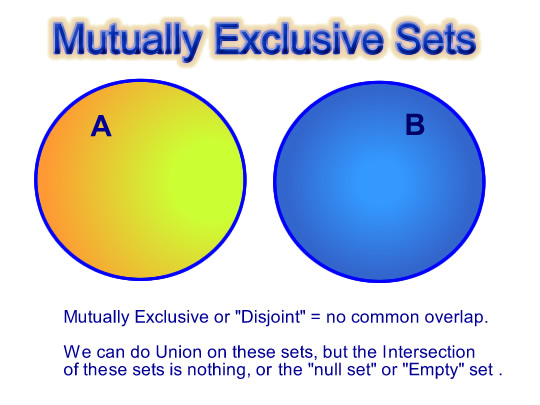
Image Source: Passy’s World of Mathematics
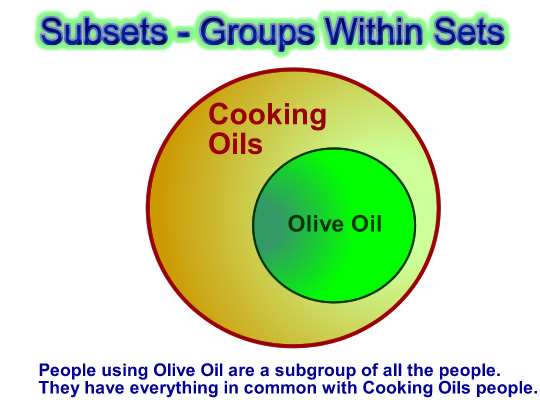
Image Source: Passy’s World of Mathematics
Videos About Venn Diagrams
The following is a good example of how Intersection and Union work in Venn Diagrams.
Here is a short video about Intersection
Here is a musical video showing Intersection. It is a bit out there but gets the point across.
Here is a Video all about Union of sets.
Here is a Video all about Set Notation.
Here is a video which shows some more advanced aspects of Intersection of sets.
Related Items
Venn Diagram Word Problems
Three Circle Venn Diagrams
Real World Venn Diagrams
If you enjoyed this post, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our blog, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Introduction to Venn Diagrams” Powerpoint.
Enjoy,
Passy













Pingback: Venn Diagram Word Problems | Passy's World of Mathematics
Pingback: Three Circle Venn Diagrams | Passy's World of Mathematics
Pingback: Real World Venn Diagrams | Passy's World of Mathematics
Pingback: Venn Diagrams Introduction | Education and Technology for Future