
Image Source: http://s3.amazonaws.com
If trying to solve math equations is driving you to tears, then “The Onion Skin” methods might help make your life a bit easier.
It’s like a pair of goggles that will clear everything up for you, and make you feel happy again!
Passy only discovered this method recently, by seeing a teacher called Nadia, who works with Passy, showing some students how to do this.
(Thanks for sharing this great idea Nadia).
The idea of the method, is that our variable letter is at the center of the onion, and then has skins built onto it by the operations which have been applied to it in the equation.
We then look at peeling back the skins, using reverse operations, to get back to our original variable letter.
Finally we apply these reversing operations to the number value on the right hand side of the equation.
This then gives us a numeric solution to the equation.
Basically it is just another means of doing the “Flowcharts Back-Tracking Method”, and provides a great scaffold for students who are beginners at solving Algebra Equations.
Many “Purists” are not particularly fond of these diagramatical methods. However, here at Passy World we are a firm believer in using diagrams to assist those students who are not yet at a level to work with the abstract “doing to both sides” Algebraic methods.
BODMAS/PEMDAS Order of Operations
Here is a quick review of the Operations we look for when solving Algebra Equations.

Image Copyright 2012 by Passy’s World of Mathematics
For the Equation: 2N + 5 = 11
Operations are + 5 and x2
BODMAS or PEMDAS for these is x2 then + 5
Here are the “Opposite Operations” we need to know when solving Equations.

Image Copyright 2012 by Passy’s World of Mathematics
For our previous example: 2N + 5 = 11
1) Operations are + 5 and x2
2) BODMAS or PEMDAS for these is x2 then + 5
3) Opposites are /2 and -5
Onion Skin Methods for Equations
In this lesson we look at two “Onion Skin” methods for solving Algebra Equations.
The first method uses a flowchart type diagram containing two onions, which we call the “Double Onion Method”.
The second method is a quicker method, that uses only one onion, and is called the “Single Onion Method”.
We recommend starting off using the “”Double Onion Method”, but then upgrading to use the quicker “Single Onion Method” as soon as you are comfortable to do so.
Double Onion Method
The “Double Onion Method” involves drawing two identical onions next to each other, and following through a set of working out steps in a specific order.

Image Copyright 2012 by Passy’s World of Mathematics
The following diagrams show how to work through these steps for the simple equation: n + 5 = 7
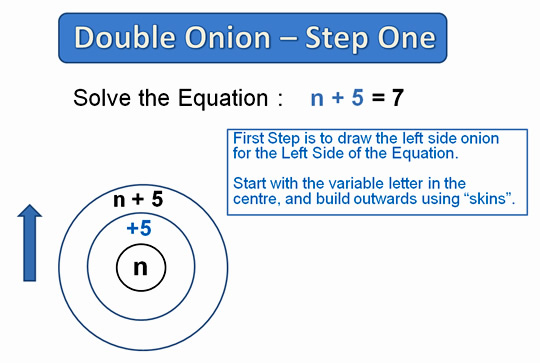
Image Copyright 2012 by Passy’s World of Mathematics
If the onion skins have been done correctly, then working outwards from the centre, the operations should be in BODMAS/PEMDAS oder.
Here are the remaining steps of the working out.
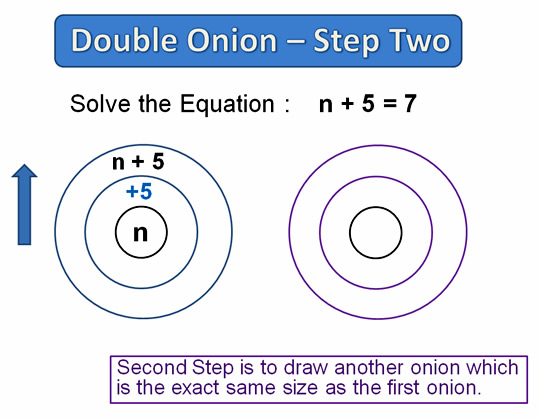
Image Copyright 2012 by Passy’s World of Mathematics
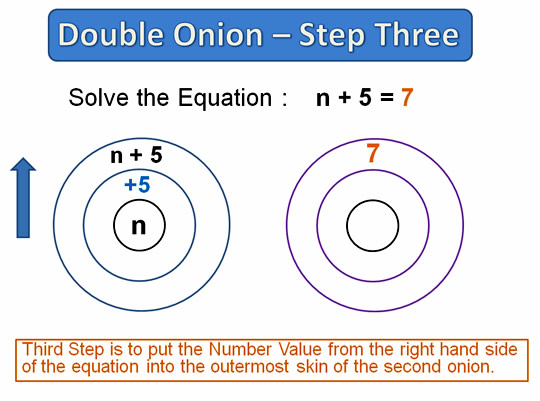
Image Copyright 2012 by Passy’s World of Mathematics

Image Copyright 2012 by Passy’s World of Mathematics
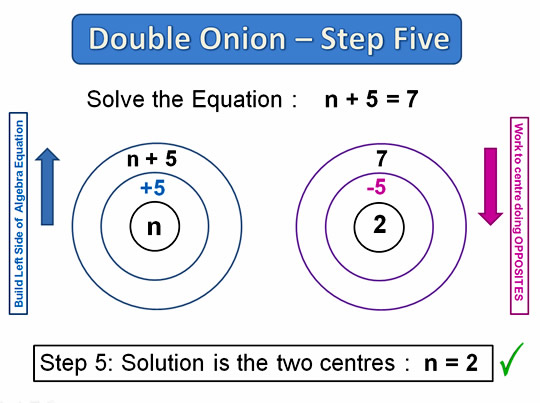
Image Copyright 2012 by Passy’s World of Mathematics
Double Onion Two Step Equations
The following diagram shows a fully worked example of using the two onion method for a two step Equation.
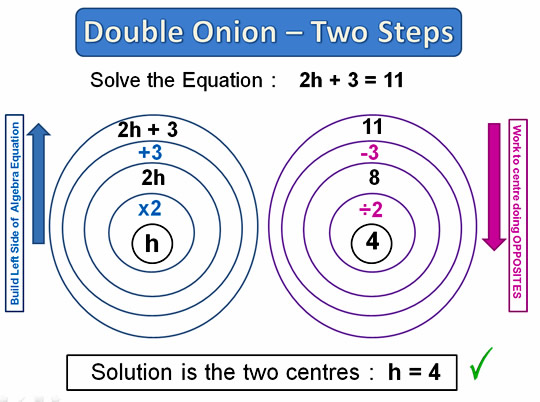
Image Copyright 2012 by Passy’s World of Mathematics
Note that the + – x / operations inside the left hand onion should always go from the centre outwards in BODMAS/PEMDAS Order.
The next fully completed example is for a two step equation which contains brackets.

Image Copyright 2012 by Passy’s World of Mathematics
Note that the + – x / operations inside the left hand onion should always go from the centre outwards in BODMAS/PEMDAS Order.
Single Onion Method
The “Single Onion Method” is a quicker method, which uses only one onion.
It is recommended to learn the “Double Onion Method” first, and then progress on to use this single onion method.
The single onion method involves drawing onion rings around the equation which needs to be solved.
These onion skins are created by first drawing a centre skin around the letter variable.
We then create skins outwards from here, following the BODMAS/PEMDAS order of operations.
The outermost skin should enclose the entire equation.
Here is a single onion diagram for our previous example equation:
N + 5 = 7

Image Copyright 2012 by Passy’s World of Mathematics
To solve the Equation, we work from the biggest outer skin, inwards through the smaller skins, applying opposite operations, until we reach the central letter variable.
The following diagram shows our completed equation solution.

Image Copyright 2012 by Passy’s World of Mathematics
Single Onion Method Examples
The following are some fully completed Single Onion Method questions.
They show the onion diagram, followed by the application of the “opposite operations”, to reach the final solution answer.

Image Copyright 2012 by Passy’s World of Mathematics

Image Copyright 2012 by Passy’s World of Mathematics

Image Copyright 2012 by Passy’s World of Mathematics
It is very important when doing the reversing steps, that they are done without a calculator, in the exact order that the “peeling” inwards occurs.
From the onion methods, it should not be too hard to later move to the non-diagram Algebraic working out of equations.
The onions are a handy helper for equations, and generate the reverse order steps, which are essential for solving equations.
The starting onion can be used to work out the reverse operations, and then the normal algebraic operations to both sides steps can be done on the actual equation. The degree to which the diagrams are used is really up to the skill level of the individual student.
Factorising Using an Onion Skin Method
There is also an Onion type method that can be used for finding factors of numbers.
This is demonstrated in the following video.
Boom Crash Opera – Onion Skin
Finally, (for no particular mathematical reason whatsoever), here is one of Passy’s all time favorite songs called “Onion Skin”, by Australian Band “Boom Crash Opera”.
Related Items
How to Translate Word Problems into Equations
Solving One Step Addition Equations
Solving One Step Subtraction Equations
Solving One Step Equations – All Types
Two Step Equations Using Flowcharts and Back Tracking
Two Step Equations Using Reverse Operations
Three Step Equations Using Flowcharts and Back Tracking
Balance Beam Equations
Equivalent Equations
Fractions Equations
Solving Equations Word Problems
eBay Problem Solved Using Algebra Equations
Microsoft Mathematics Equations Solver
Real World Mathematics Formulas and Equations
Equations Games
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Enjoy,
Passy



Pingback: Transposing and Rearranging Formulas | Passy's World of Mathematics
Pingback: Variable On Both Sides Equations | Passy's World of Mathematics