Image Source: http://www.howitworksdaily.com
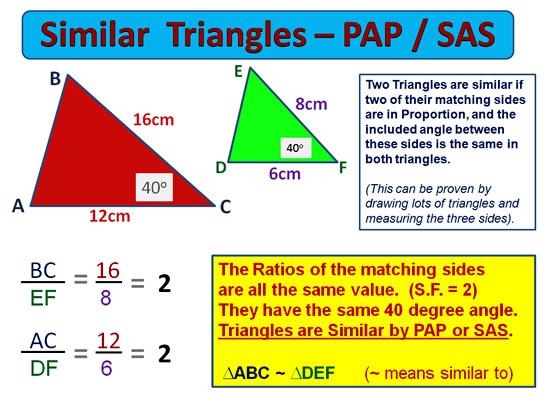
A powerful Zoom lens for a 35mm camera can be very expensive, because it actually contains a number of highly precise glass lenses, which need to be moved by a tiny motor into very exact positions as the camera auto focuses.
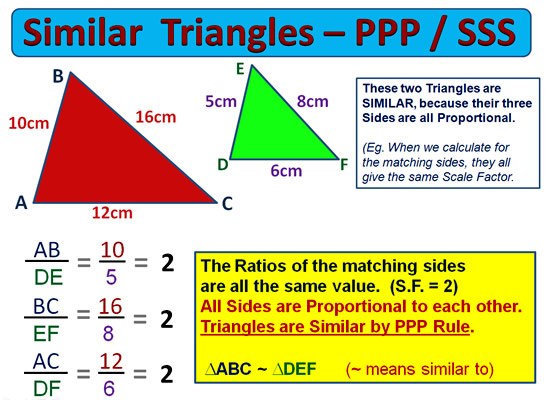
The Geometry and Mathematics of these lenses is very involved, and they cannot be simply mass produced and tested by computer robots.
Lots of effort required to manufacture these lenses results in their very high price tags.
Here is a diagram showing how the zoom lens internal arrangement changes as we zoom from 18mmm wide angle to 200mm fully zoomed in:

Image Source: http://www.canon.com

Image Copyright 2013 by Passy’s World of Mathematics
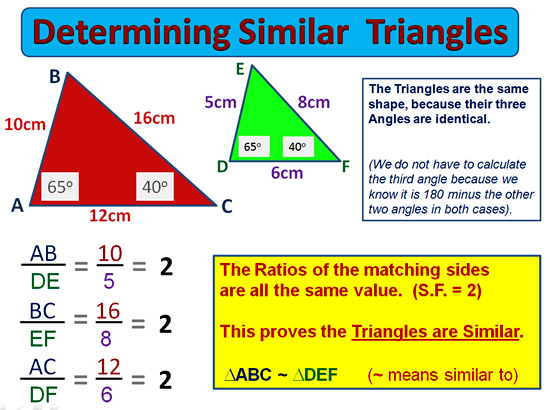
Shown above are some band photographs taken by Passy with a special low light camera.
Unfortunately this camera does not have a zoom lens, and so you need to be right up close to the stage to take good pictures.
A special low light aperture 1.4 zoom lens for taking band photographs has a price tag a bit out of Passy’s current reach.
The light rays passing through a camera lens involves some similar triangles mathematics.
We will do some of this mathematics in the “Bow Tie” examples later in this lesson.
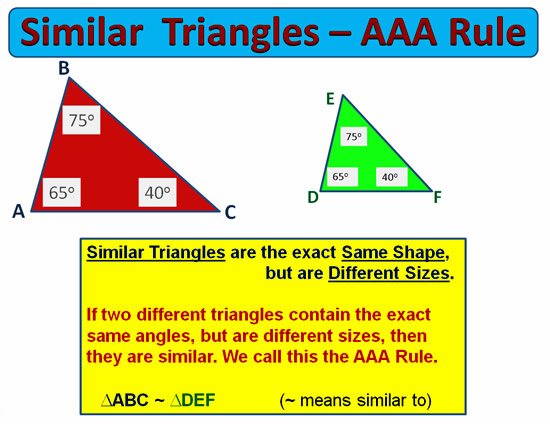
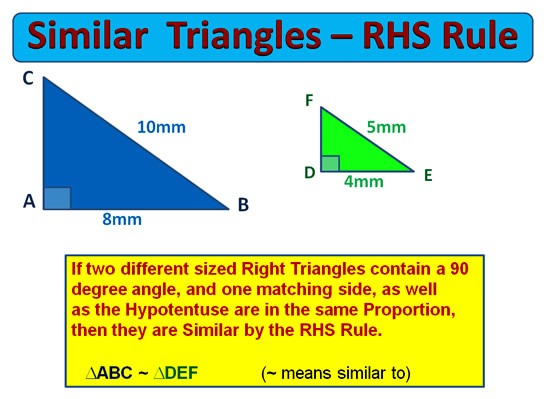
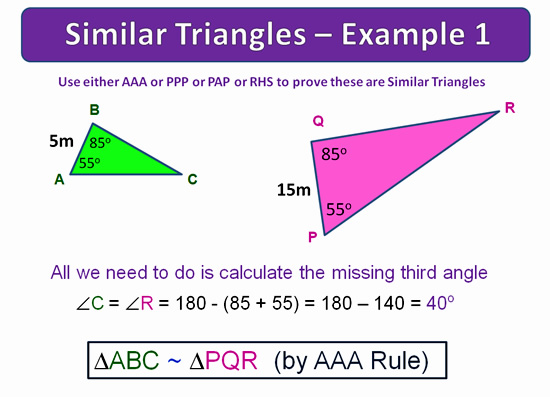
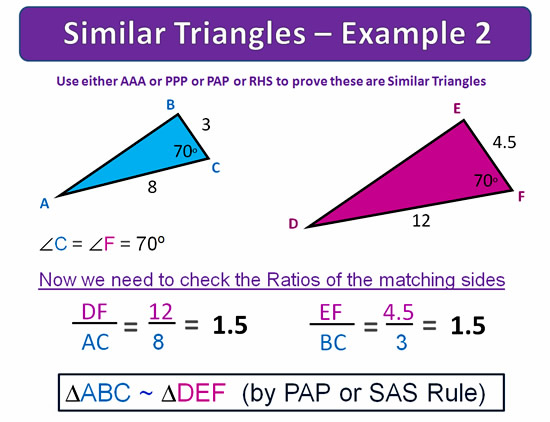
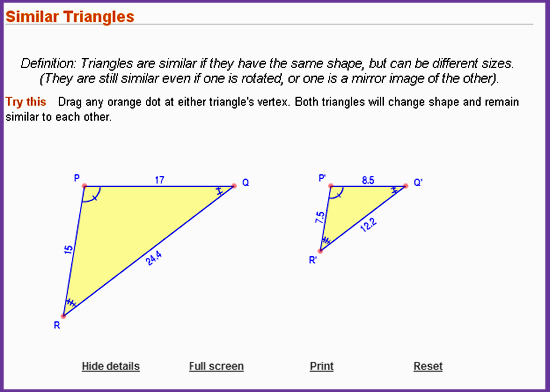
Similar Triangles can also be used to measure the heights of very tall objects such as trees, buildings, and mobile phone towers.
Measuring heights of tall objects is also covered in this lesson.
It is very important that you have done our basic lesson on Similar Triangles before doing the lesson which follows on here.
If you need to go back and look at Basic Similar Triangles, then click the link below:
Similar Shapes and Similar Triangles
Bow Tie Triangles
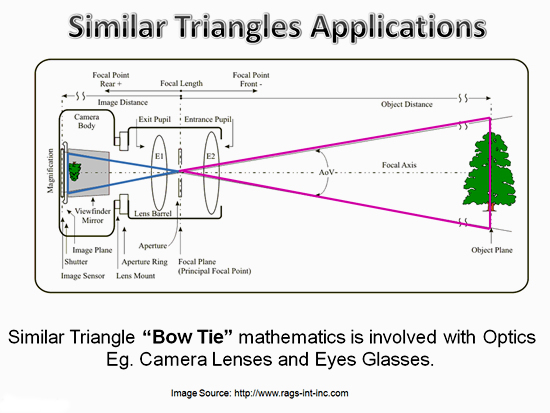
Image Copyright 2013 by Passy’s World of Mathematics
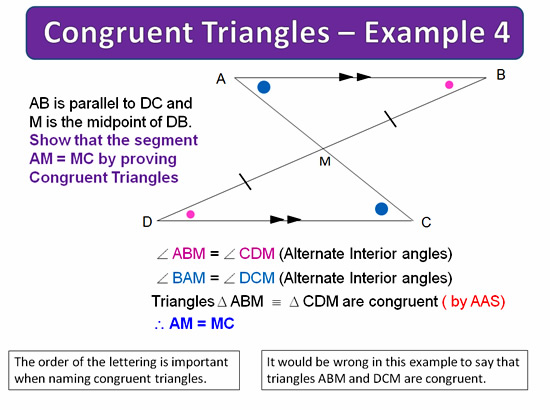
In the above setup for a camera lens, we have a “Bow Tie” shaped pair of Similar Triangles.
Note that when light passes through a camera lens the original image ends up upside down or “inverted”.
This is why cameras have a mirror inside them to put the image right way up so we can view it while taking the photo.
It is very important that this mirror is kept spotlessly clean when changing lenses on a 35mmm camera, and we must be careful never to touch it with our fingers.
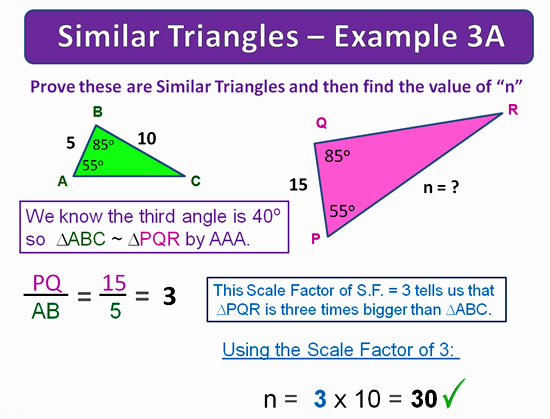
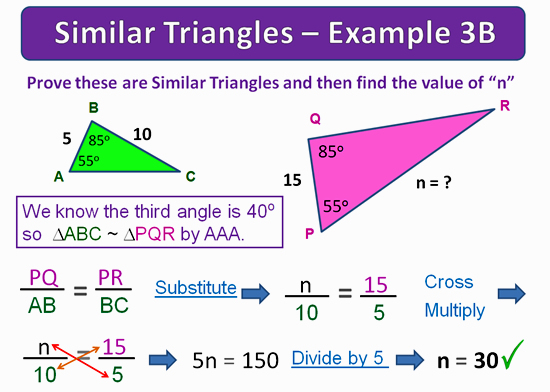
Bow Tie Example 1A
The diagram below shows the triangles from our camera lens diagram, with some measured values labelled onto it.
We have used two of the the measurements to work out the “Scale Factor”.
Once we have the S.F. we can then easily work out our missing value.

Image Copyright 2013 by Passy’s World of Mathematics
We do not have to use the Scale Factor method to work out this question.
Instead, we can use the Ratios Cross Multiplying Method, as shown in “Example 1B” below.
It is up to you as to which method you want to use. Both methods give the same correct answer.
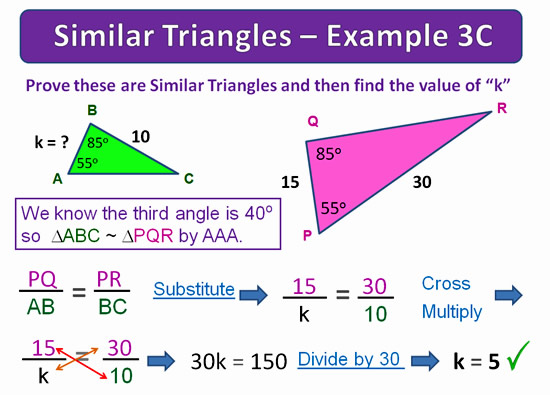
Bow Tie Example 1B
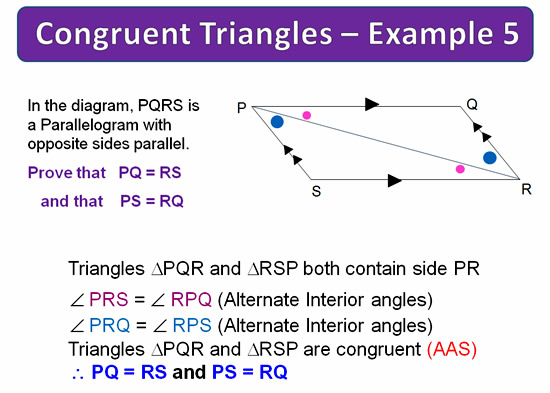
In this example we first locate our two pairs of matching sides on the given diagram below.
We then set them up as matching ratios, and use the ratios cross multiplying method to get our answer.
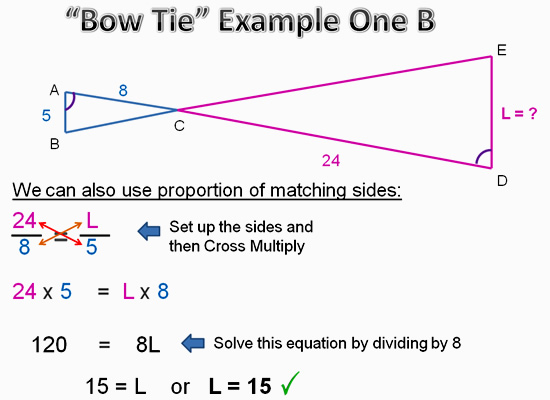
Image Copyright 2013 by Passy’s World of Mathematics
Bow Tie Example 2
Here is another example where we are working with “Bow Tie” Similar Triangles.

Image Copyright 2013 by Passy’s World of Mathematics
In the above example we have used the Scale Factor Method.
This question can also be worked out using cross multiplied ratios, if you prefer to use that method instead.
Video About Bow Tie Questions
The following video shows how to do some example Bow Tie and Ladder Triangle questions.
Using Triangles to Find Height
Similar Triangles can also be used to work out the Heghts of tall objects such as trees, buildings, and towers which are too hard for us to climb and measure with a measuring tape.
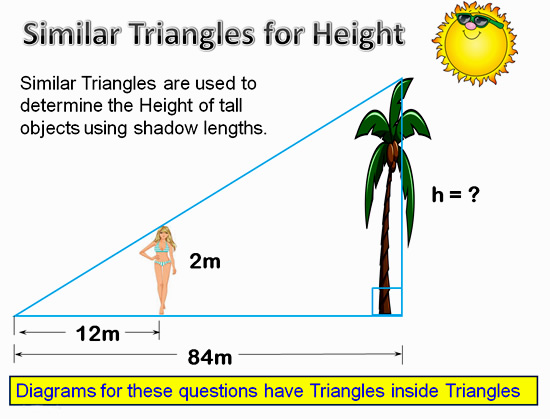
Image Copyright 2013 by Passy’s World of Mathematics
Because the sun is shining from a very long way away, it shines down at the same angle on both objects (the person and the tree).
Shadows are formed for both of these objects, because the sun is shining on them at an angle.
Eg. The 2m tall lady makes a 12m long shadow, and the palm tree makes an 84m long shadow.
This results in a pair of similar triangles being formed.
By comparing the lengths of the two shadows, against the two heights, using similar triangles, we can work out the unknown height of the tree.
In the following two examples we show how these types of height questions are drawn as a triangle inside a triangle.
We then use the Scale Factor Method to get our answer for “Example 1A”.
After this, we do the same question using the Cross Multiplying Ratios Method in “Example 1B”.
Finding Height – Example 1A

Image Copyright 2013 by Passy’s World of Mathematics
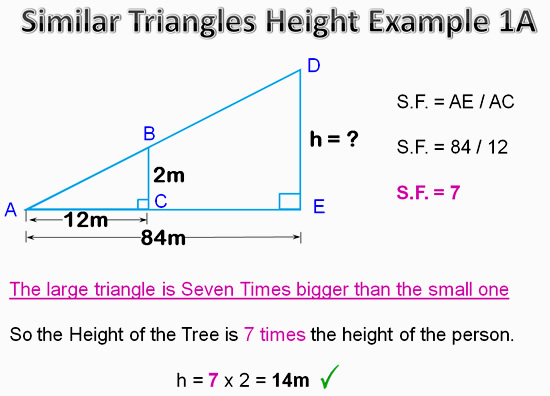
Image Copyright 2013 by Passy’s World of Mathematics
Finding Height – Example 1B

Image Copyright 2013 by Passy’s World of Mathematics
Finding Height – Example 2
Here is another example of finding height from the shadows, but this time we have a Mobile Phone Tower, and a shorter person with a smaller shadow.
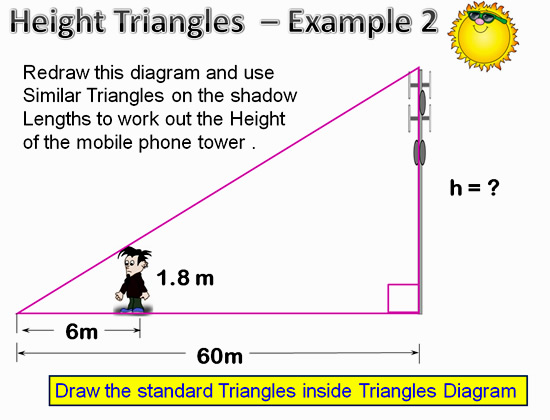
Image Copyright 2013 by Passy’s World of Mathematics
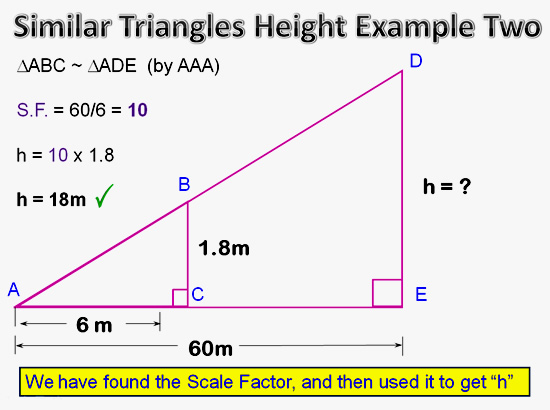
Image Copyright 2013 by Passy’s World of Mathematics
In the above example we have used the Scale Factor Method.
This question can also be worked out using cross multiplied ratios, if you prefer to use that method instead.
Videos About Finding Height
Three and a a half minute video about using shadows to find the height of a tree:
Ten minute video showing a guy actually finding the height of a wall using shadows:
Video showing some algebra x and y problems:
Finding Height Using a Mirror
We can also find the height of a tall object by using line of sight and a mirror, rather than measuring shadows.
This gives a “Bow Tie” type question that we need to solve.
The video at the following link shows an example fo how to do this.
Click here for Video About Finding Height Using a Mirror
River Width Example
Similar Triangles are very useful for indirectly determining the sizes of items which are difficult to measure by hand.
Typical examples include building heights, tree heights, and tower heights.
Similar Triangles can also be used to measure how wide a river or lake is.
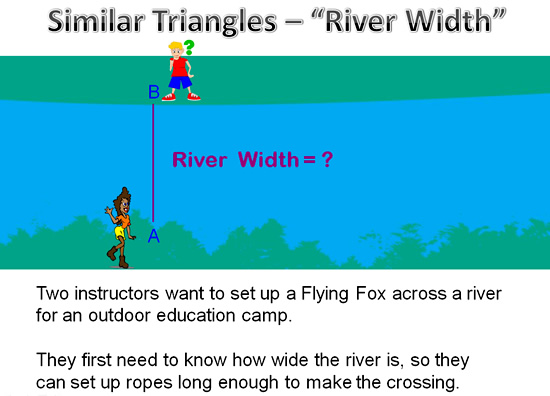
Image Copyright 2013 by Passy’s World of Mathematics
Now the instructors could toss a coin to see who ties a rope to themselves, and then swims across the freezing cold water to work out how wide the river is.
However, the following method shown here is much easier, and nobody has to get wet!
It involves each person moving further along the river and measuring exactly how far they have moved from their starting points at A and B.
This is shown in the following diagram:
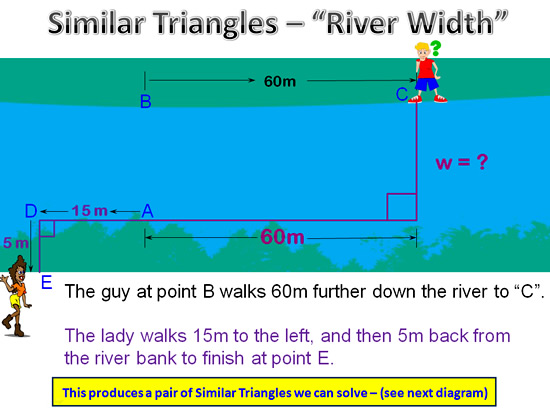
Image Copyright 2013 by Passy’s World of Mathematics
We can draw in the line of sight from the lady at “E” to the guy on the other side of the river at “C”, which then produces a pair of Similar Triangles.
We can solve these “bow tie” triangles and work out the width of the river as shown below.
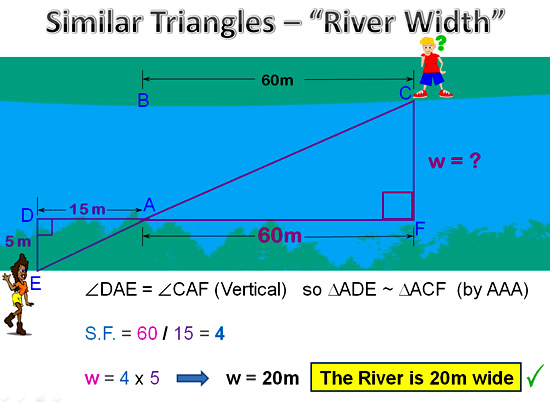
Image Copyright 2013 by Passy’s World of Mathematics
(Note that some clipart images from the web were used for the above River Diagrams, and Passy’s World is not claiming any ownership of these cliparts, but only of the mathematical components contained in these examples.)
Related Items
Tall Buildings and Large Dams
Similar Shapes and Similar Triangles
Geometry in the Animal Kingdom
Mathematics of Sharks
Classifying Triangles
Angle Sum in a Triangle
Exterior Angle of a Triangle
Angles and Parallel Lines
Pythagoras and Right Triangles
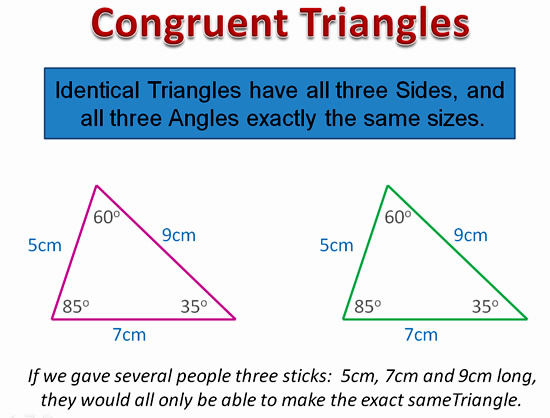
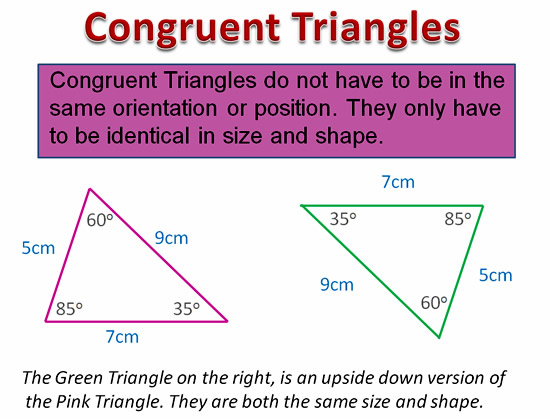
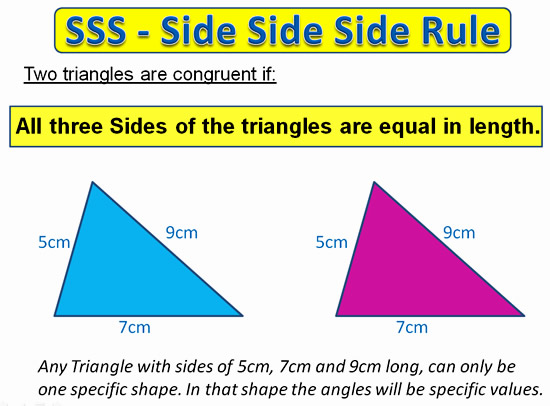
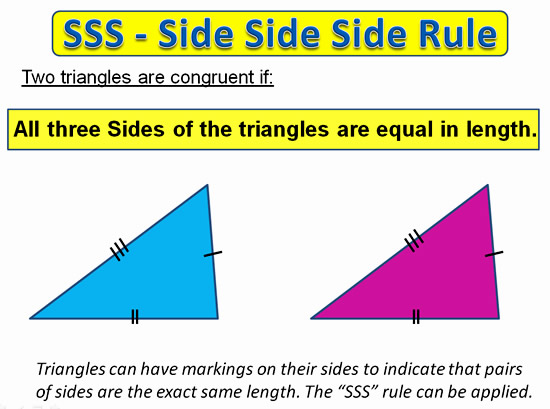
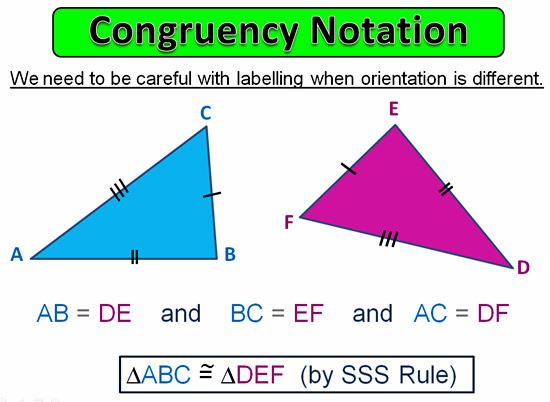
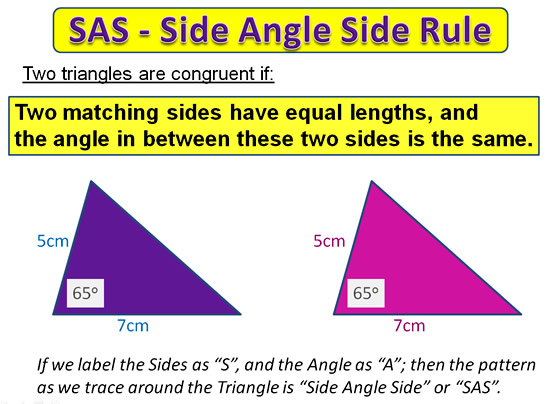
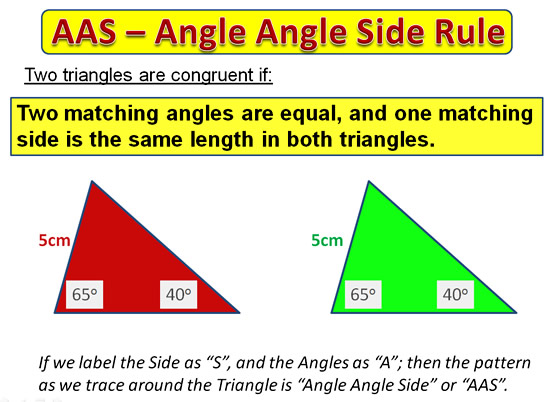
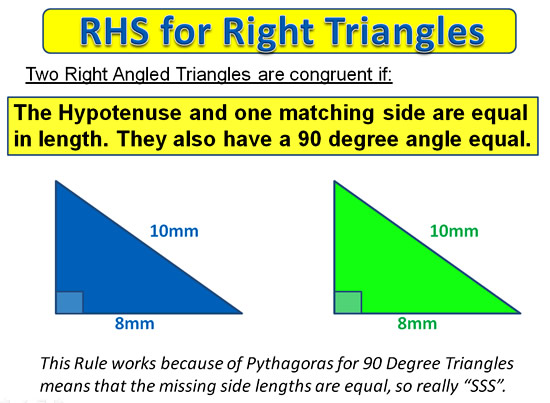
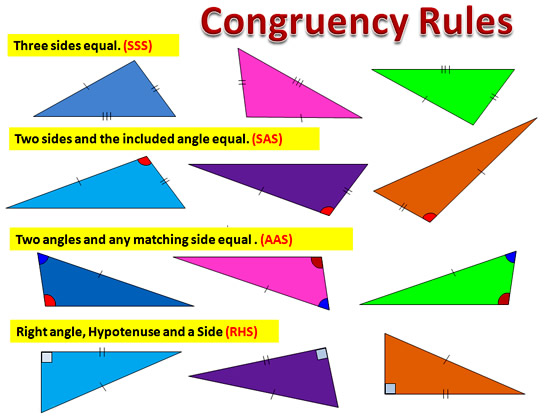
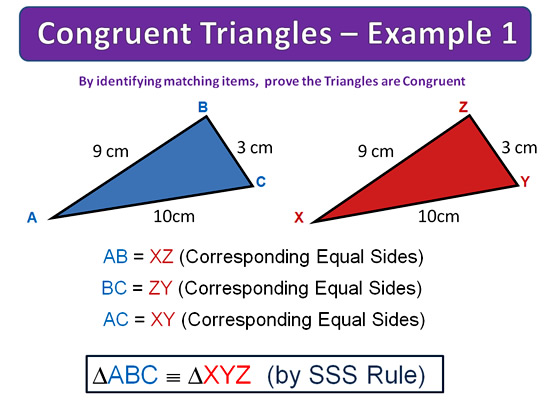
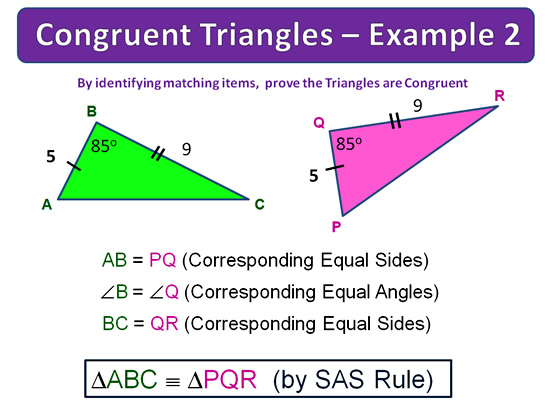
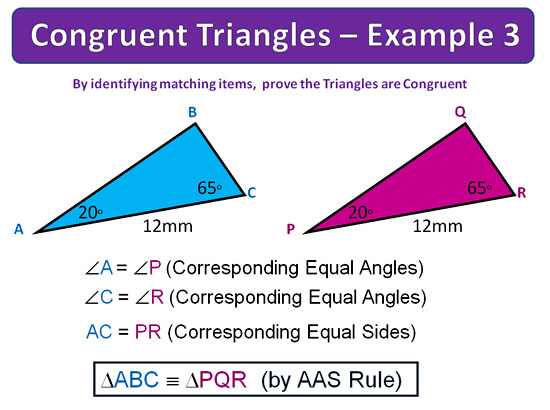
Congruent Triangles
Subscribe
If you enjoyed this lesson, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Go to the subscribe area on the right hand sidebar, fill in your email address and then click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
If you would like to submit an idea for an article, or be a guest writer on our website, then please email us at the hotmail address shown in the right hand side bar of this page.
If you are a subscriber to Passy’s World of Mathematics, and would like to receive a free PowerPoint version of this lesson, that is 100% free to you as a Subscriber, then email us at the following address:
Please state in your email that you wish to obtain the free subscriber copy of the “Similar Triangle Applications” Powerpoint.
Feel free to link to any of our Lessons, share them on social networking sites, or use them on Learning Management Systems in Schools.
Like Us on Facebook
Help Passy’s World Grow
Each day Passy’s World provides hundreds of people with mathematics lessons free of charge.
Help us to maintain this free service and keep it growing.
Donate any amount from $2 upwards through PayPal by clicking the PayPal image below. Thank you!
PayPal does accept Credit Cards, but you will have to supply an email address and password so that PayPal can create a PayPal account for you to process the transaction through. There will be no processing fee charged to you by this action, as PayPal deducts a fee from your donation before it reaches Passy’s World.
Enjoy,
Passy