Image Source: http://www.urukia.com
In this lesson we look at finding the biggest values of two measurements: Height and Volume.
For height we look at the world’s tallest buildings, and for volume we look at the world’s biggest dam.
Big Buildings – Biggest Height
The Burj Dubai, which was later renamed as the Burj Kahlifa, is currently the tallest building in the world, at around 800m in height.
It certainly is tall. Passy’s World visited the Burj in September 2010, and the elevators were especially amazing. Inside you don’t even feel the motion, even though they are speeding upwards at 80km/hr! It takes only a minute in the elevator to reach the top. These elevators are one of a kind, especially made for the Burj. Making them involved some very clever mathematics and engineering.
The view from the top is truly breathtaking.
The Burj Khalifa is certainly a lot taller than the world’s other tallest buildings.

Image Source: http://www.ideapharmer.com
There was some challenging engineering and mathematics problems to be solved when building the Burj Khalifa.
First of all some revolutionary new geometry was used to create a unique Y-shaped footing for the building. The building’s external geometric shape was also a revolutionary new design that disperses high speed desert winds, and stops the building from twisting. There were also special challenges getting the glass cladding and windows to fit perfectly onto this unique building shape. Mathematics and specially adapted GPS, were both used during construction to make sure the building stayed perfectly straight, or “plumb”.
The following video shows some of the unique features of the building of the Burj Dubai, as well as the famous sail shaped island hotel in Dubai.
[youtube http://www.youtube.com/watch?v=1bOd_v7Ukgw]
Another challenge for engineers building the world’s tallest buildings is protecting them against earthquakes.
The first two minutes of the following video shows how an earthquake proof geometry and design was used for the Taipei 101 building. This design was even put to the test during the construction of the building, when an earthquale actually occurred, as shown in the video.
[youtube http://www.youtube.com/watch?v=Q2o6jBcjBL0]
Measuring the Heights of Structures
How do we Measure the Height of something that is very tall?
There are two main traditional mathematical methods for doing this.
The first method involves using the shadows and the mathematical construct of “Similar Triangles”. In this method we compare the shadow of an object of known height, such as a broom, with the shadow length of the structure.

Image Source: http://images.brighthub.com
The second method involves making a 45 degree angle inclinometer, or “clinometer”.
From the mathematics of Triangles, if we can get the viewfinder of our clinometer, (which is just a drinking straw), to line up with the top of a structure, then we know the height of the object is the same as the distance we are from the base of the object. This uses the mathematical fact that an equilateral 45 degree right triangle has equal sides.

Image Source: http://images.brighthub.com
There is also a third mathematical method that involves Trigonometry, where we can use angles other than 45 degrees for the inclinometer, and then work out the height using the Tangent of the incline angle, multiplied by how far we are from the base of the building.
However, in the modern age of computers and laser beams, we could use a laser rangefinder to determine height, provided that we can get positioned on the very top of the building, or position a helicopter alongside the top of the building.
A laser rangefinder is a device which uses a laser beam to determine the distance to an object. The most common form of laser rangefinder operates on the“time of flight” principle. This involves sending a laser pulse in a narrow beam towards the ground and measuring the time taken by the pulse to be reflected off the ground and returned to the top of the building. By knowing the speed of the light beam, the Distance can then be calculated.
In our measurement of things that are very big, let’s now look at the biggest volume of liquid that humans have ever managed to get into a container.
The Three Gorges Dam

Image Source: http://www.project-resourceblog.co.uk
The Three Gorges Dam in China is the undisputed winner of the biggest volume prize, as it is far ahead of any other volume of water in the world that has ever been contained by humans.
The Three Gorges Dam crosses the Yangtze River in Hubei province in China. It the world’s largest hydroelectric power station by total capacity, which is 22,500 MW at full power. When the water level is maximum at 175 meters (574 ft) over sea level (91 meters (299 ft) above river level), the reservoir created by the dam is about 660 kilometers (410 mi) in length and 1.12 kilometers (0.70 mi) in width on average. The total surface area of the reservoir is 1045 square kilometers, and it could flood a total area of 632 square kilometers, of land. The reservoir contains about 39.3 cu km (9.43 cubic miles) of water. That water weighs more than 39 trillion kilograms (42 billion tons).
Information source: http://www.businessinsider.com
The volume of the water in Port Phillip Bay in Melbourne Australia is around 25 cubic kilometres (6.0 cu mi). So the Three Gorges Dam created on the Yangtze River in China is about one and a half times bigger than the Bay.
While the dam was being built to harness the flow of the Yangtze River, a set of locks had to be built as well, in order to allow the large amounts of shipping traffic on the river to continue to use the river.

Image Source: http://upload.wikimedia.org
Here is a short video all about the Three Gorges Dam.
[youtube http://www.youtube.com/watch?v=e_VnEMzak4Q]
Hydroelectricity involves holding back a large mass of water, and then letting it run down huge pipes to a lower level. The energy of the falling water is used to spin around huge turbines. These spinning turbines then generate electricity.
The greater the difference in river height created by the dam, the greater the distance the water falls, and the more energy available to make electricity.
The earth’s gravity is what makes the water fall, and is the source of the energy.
The math equation involved is : Energy = 9.8 x Mass x Height.
9.8 is the earth’s gravitational force constant, and the Mass of water flowing down into the turbine is extremely large. This combined with the average 150m to 175m height of water in the dam, creates a very large amount of Energy.
The percentage efficiency of the electricity generation is an amazing 90%.
Eg. 90% of the gravitational energy of the water falling is harnessed to create electricity.
Here is a diagram of how Hydroelectricity works.
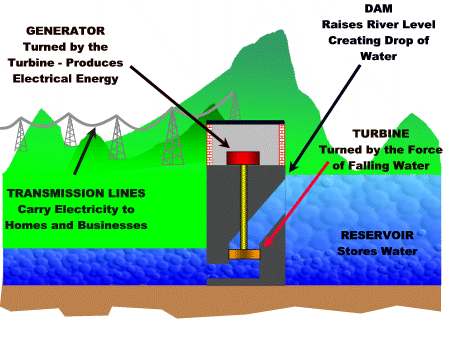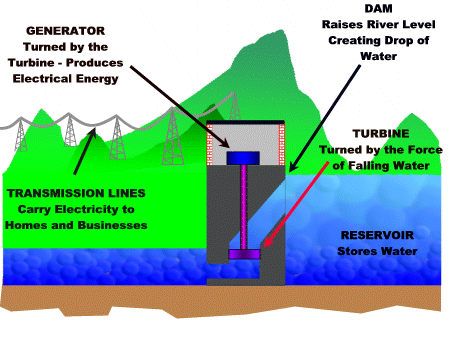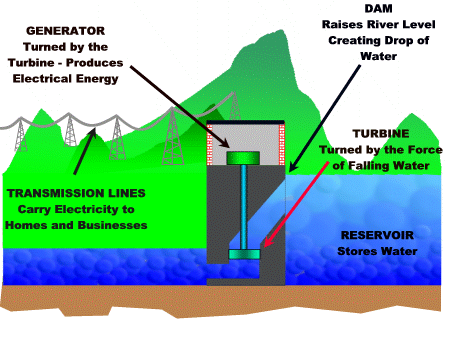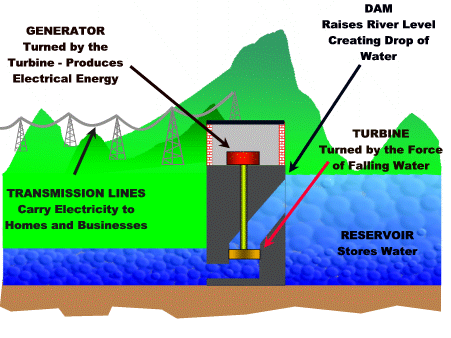
Image Source: http://earthsci.org
Shown below is a picture taken during the building of the Three Gorges Dam, showing where the massive turbines are located deep inside the dam’s structure.

Image Source: http://freeassociationdesign.files.wordpress.com
There would have been a lot of mathematics involved with working out just how big they could make the internal pipes, and the turbines, to the largest size possible, to generate the most electricity. They would also have to consider and calculate how many pipes they could put through the dam wall without compromising its strength. This is all part of the exciting mathematical work that Engineers do when designing structures and machines.
As dams are made higher, they have to be made strong enough to hold back the massive volume of water that is behind the dam wall.
The shape of a dam was is usually thinnest at the top and very thick at the bottom. The geometric shape is that of a three dimensional skewed Trapezium.
The far side of the dam needs to be made much bigger and thicker than the wall side, as it needs to counteract the huge weight of water behind the dam wall. This is shown in the following picture.

Image Source: http://www.sai.uni-heidelberg.de
Whilst providing a massive amount of electricity, the Three Gorges dam in China is having a number of problems currently in 2011.
The slowing down of the old river’s flow of water behind the dam has lead to lots of Algae pollution, and lots of rubbish piling up behind the dam. It actually costs the dam operators 1.5 million dollars a year to remove the rubbish from behind the dam wall.
However, the main idea of the dam was to create green electrical energy that does not cause carbon emmissions, and to this end it has been successful. It has also been used to control and prevent downstream flooding of the Yangtze River during periods of heavy rainfall.
It certainly is an amazing feat of mathematics and engineering.
Related Items
Sydney Harbour Bridge Mathematics
Perimeter
Circumference
Area of Simple Shapes
Area of a Circle
Interesting Circles
Composite Areas
Measurement Formulas
My Virtual Home
If you enjoyed this post, why not get a free subscription to our website.
You can then receive notifications of new pages directly to your email address.
Just find the subscribe area on the right hand sidebar, fill in your email address and click the “Subscribe” button.
To find out exactly how free subscription works, click the following link:
Enjoy,
Passy